IV. Трансцендентные звенья.

Звено чистого (транспортного) запаздывания.

 - скорость перемещения ленты;

Q₁ – объем сыпучего продукта в единицу времени ,подается через шибер;

Q₂ – выход продукта.

Время чистого запаздывания .

В природе нет ни одного процесса без чистого запаздывания.

преобразуем по Лапласу это выражение (теорема запаздывания), получим отсюда

Аппроксимация, соответствующая n=2 при применении функции pade, Т=1с:

.

Рассмотренные выше наиболее часто встречающиеся на практике основные типы звеньев характеризуются отсутствием корней с положительной вещественной частью уравнений числителя (т.е. нулей передаточных функций) и знаменателя (т.е. полюсов) называются МИНИМАЛЬНО-ФАЗОВЫМИ. Из всех возможных звеньев с одинаковыми амплитудными характеристиками минимально-фазовые звенья обладают наименьшими по абсолютным значениям фазовыми характеристиками; второе их важное свойство – однозначное соответствие амплитудной и фазовой частотных характеристик (т.е. по амплитудной характеристике можно определить фазовую и наоборот.

- неминимально-фазовое звено.

Передаточные функции систем различной структуры

1. Последовательное соединение звеньев.

Пусть

тогда а

При последовательном соединении звеньев передаточная функция системы равна произведению передаточных функций звеньев, входящих в систему.

Переходная характеристика системы не может быть найдена из переходных характеристик звеньев она определяется специальными методами.

Так как известны передаточные функции звеньев, то известны и частотные

функции звеньев Wi(j),

тогда

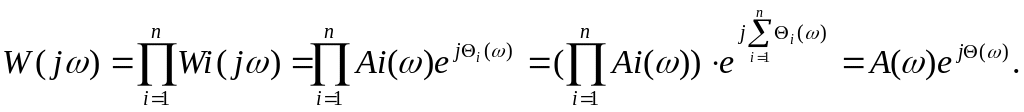
2. Параллельное включение звеньев.

Определим передаточную функцию системы:

2. Встречно-параллельное соединение динамических звеньев.

3.1. Контур с отрицательной обратной связью.

С оставим систему уравнений

контура:

Тогда

• передаточная функция контура с отрицательной обратной связью.

Контур с неединичной обратной связью может быть преобразован к контуру с единичной отрицательной обратной связью

где

Эквивалентная структурная

схема контура с ООС.

3.2. Контур с положительной обратной связью.

где

Преобразование структурных схем

Используется для упрощения анализа и синтеза САУ, составления передаточных функций и дифференциальных уравнений. Преобразования схем проводят так, чтобы контуры не пересекались, а чтобы один контур входил внутрь другого. Закон изменения выходного сигнала не должен изменяться в результате эквивалентного преобразования структуры.

Исходная структура системы	Эквивалентная структура системы
Перенос точки суммирования сигналов со входа на выход. Уравнение выходной координаты:	Wф(p) - фиктивная передаточная функция
Перенос точки суммирования сигналов с выхода звена на его вход. Уравнение выходной координаты:
Перенос точки съема сигнала со входа звена на его выход.

U(p) Y(p) Y(p) W(p) Перенос точки съема сигнала с выхода на вход звена.
Перестановка сумматоров.
Вынос точки разветвления из встречно-параллельного соединения.

Пример1. Определить передаточную функцию системы заданной структуры путем эквивалентных преобразований к одному звену.

Исходная структурная схема:

Y

U

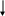
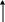
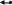
W₅

W₁

W₂

-

W₃

W₄

а

W_2,3

Разделение сумматоров

Y

U

) разделение сумматоров:

W₅

W₁

W₂

W₃

б) объединение элементов контура:

W₅

Y

U

W_2,3

W₁

W₄

в) переносим точку суммирования сигналов:

=

г) объединение последовательно включенных звеньев и перестановка сумматоров:

W_1,5=W₁+W₅

д) объединение звеньев контура и последовательно-параллельных звеньев:

е) объединение последовательно-соединенных звеньев:

Пример2. Преобразовать заданную структурную схему по каналу возмущения с целью приведения ее к удобному виду для пользования номограммой замыкания.

Исходная структурная схема: F - возмущающее воздействие. Найти передаточную функцию по каналу возмущения предполагая R(p)=0 (входное воздействие отсутствует).	Преобразуем схему: а) W1 для  находится в обратной связи. б)
г) ЛЧХ контура с единичной отрицательной обратной связью можно найти по ЛЧХ разомкнутой системы с использованием номограммы замыкания.	в)