4.2 Зависимость подвижности носителей заряда от напряженности электрического поля; критическое поля.

Рис. 1. Зависимость подвижности (а) и скорости движения носителей заряда от напряженности электрического поля (б)

Область I соответствует постоянству подвижности носителей заряда. С помощью формулы , получили зависимость на рис. 1, б. Поскольку то

, т.е. растет линейно с ростом E. Область I называется облас­тью слабых полей, или линейной областью. В этой области постоянство подвижности в сочетании с постоянством концентрации носителей заряда обеспечивает постоянство проводимости (и удельного сопро­тивления) твердого тела. Область II называется областью закритических полей, или нели­нейной областью. Здесь, поскольку с ростом E не меняется скорость движения носителей заряда, происходит уменьшение проводимости твердого тела (увеличение удельного сопротивления). При этом, как и в области I, концентрация носителей заряда остается неизменной. Напряженность поля Е_КР, разделяющая эти две области, носит название критической напряженности электрического поля. Поле Е_КР является характеристикой и проводников, и полупроводников, и диэлектриков. Критическая напряженность зависит от природы полупроводника, температуры и концентрации примеси.

4.3 Подвижность, обусловленная рассеянием на ионизированных центрах. Её зависимость от температуры и концентрации примеси.

Основная причина, вызывающая рассеяние носителей заряда при рассмат­риваемом механизме, - это кулоновское взаимодействие носителей заряда и за­ряженного центра в кристаллической решетке твердого тела.

Количество столкновений, необходимых для полного рассеяния носи­теля заряда, составляет

г де 𝜀_r - относительная диэлектрическая проницаемость твердого тела, а ze величина заряда ионизованной примеси (центра рассеяния).

Для невырожденного газа носителей заряда

Тогда и

Для вырожденного газа носителей заряда и от температуры не зави­сит. При этом 𝜇_if = const и также от температуры не зависит.

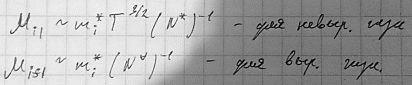Длина l_iи l_if от температуры в первом приближении не зависит и опре­деляется в основном концентрацией примеси.

4.4 Подвижность, обусловленная рассеянием на фотонах кристаллической решетки; её зависимость от температуры и концентрации примеси.

- для невырожденного газа; (1)

- для вырожденного газа. (2)

Для ответа на вопрос о зависимости 𝜇_Ф от температуры при рассеянии на акустических фононах рассмотрим зависимость от температуры параметров l, N и V, входящих в формулы (1) и (2).

Расстояние l для вырожденного и невырожденного газа носителей заряда должно быть одинаковым, поскольку оно определяется только концентрацией акустических фононов n_Ф: l ~

При больших температурах (больших темпе­ратуры Дебая) n_Ф ~ T; при этом

Для оценки величин N_i и N_if учтем, что при температурах, больших темпе­ратуры Дебая, импульс акустических фононов примерно равен импульсу носи­телей заряда.

Для невырожденного газа носителей заряда,

а для вырожденного газа и от температуры практически не зависит.

Объединяя в соответствии с формулами (1) и (2) соответствующие зави­симости от температуры l_Ф= F (T), N_Ф = F (T), и V_Ф = F(T), получаем для не­вырожденного газа носителей заряда

и для вырожденного газа

[Конечно, проведенная в данном разделе процедура анализа не дает возмож­ности точно рассчитать значение 𝜇_Ф. Более сложный и детальный анализ, учитывающий тепловые и другие свой­ства твердых тел, для случая невырожденного газа носителей заряда дает сле­дующее выражение для 𝜇_Ф

и носит на­звание «закона трех вторых»]