36. Сущность численного вычисления определенных интегралов.

Вычисление определенного интеграла по приведенной выше формуле называется численным интегрированием. Численное интегрирование применяют при решении различных задач, например: при определении площадей сложных геометрических фигур, определении работы сил, расчете длины траектории точки и в других случаях, когда подынтегральная функция "f(x)"задана по точкам, имеет сложное аналитическое выражение или ее первообразная не определяется аналитически. Сущность численных методов интегрирования состоит в различной замене (интерполяции) сложной подынтегральной функции на малых отрезках простой функцией, либо в представлении подынтегральной функции в виде сходящегося бесконечного ряда.

37. Классификация методов вычисления определенных интегралов

Методы численного интегрирования классифицируются в зависимости от того, заданы ли значения аргумента через равные промежутки или нет. Так методы Ньютона-Котеса требуют, чтобы значения были заданы с постоянным шагом, а методы Гаусса не налагают такого ограничения.

формула Симпсона

Методы Ньютона-Котеса

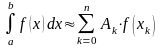
Трапеций

Ромберга

38. Влияние шага разбиения на точность вычисления определенного интеграла

Способ вычисления интеграла с автоматическим выбором шага имеет то преимущество, что он “приспосабливается” к особенностям подынтегральной функции: в областях резкого изменения функции шаг уменьшается, а там, где функция меняется слабо, – увеличивается, если пост то вычесляется по такой формуле h=(b-a)/n n элементарных отрезков

39) Сравнение методов "средних прямоугольников" и "трапеций" вычисления определенных интегралов.

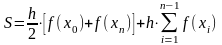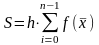По сравнению с методом прямоугольников метод трапеций более точен, так как трапеция точнее заменяет соответствующую криволинейную трапецию, чем прямоугольник. метод трапеций: метод прямоугольников: т.е. метод трапеций имеет также второй порядок, но его погрешность в два раза больше, чем в методе средних прямоугольников, поэтому, если подынтегральная функция задана аналитически, то предпочтительнее из методов второго порядка использовать метод средних прямоугольников

40) Сущность численного решения задачи Коши для оду.

Задача Коши (начальная задача): Необходимо найти такое частное решениедифференциального уравнения, которое удовлетворяет определенным начальными условиям, заданным в одной точке:

то есть, задано определенное значение независимой переменной (х₀), и значение функции и всех ее производных вплоть до порядка (n-1) в этой точке. Эта точка (х₀)называется начальной. Например, если решается ДУ 1-го порядка, то начальные условия выражаются в виде пары чисел (x₀, y₀). Численные методы решения  ОДУ различным способом аппроксимируют (приближают) значение этого интеграла для построения формул численного интегрирования ОДУ.

41) Формулировка задачи Коши решения обыкновенного дифференциального уравнения n-го порядка, 1-го порядка. Рассмотрим некоторые численные методы решения задачи Коши (начальной задачи) обыкновенных дифференциальных уравнений первого порядка. Запишем данное уравнение в общем виде, разрешенном относительно производной (правая часть уравнения не зависит от первой производной):

                                                                                      (6.2)

Необходимо найти значения функции y в заданных точках сетки  , если известны начальные значения  , где    есть значение функции y(x) в начальной точке x₀.

Преобразуем уравнение умножением на dx

И проинтегрируем левую и правую части между i-ым и i+1-ым узлами сетки.

                                                                               

Мы получили выражение для построения решения в i+1 узле интегрирования через значения x и y в i-ом узле сетки. Сложность, однако, заключается в том, что интеграл в правой части есть интеграл от неявно заданной функции, нахождение которого в аналитическом виде в общем случае невозможно.