Общий вид алгоритма оценивания
где
Условия окончания процесса последовательных приближений
Одновременное выполнение всех неравенств
Выполнение неравенства
содержит однородные компоненты
Выполнение неравенства
При нарушении условия выхода (невыполнении указанных неравенств) счетчику присваивается очередной шаг итерации и вычисления начинаются со второй точки.
Вычислетельная схема алгоритма
Задается начальная приближенная значения вектора оцениваемых параметров:
Рассчитываются элементы матрицы функции влияния
Вычисляется невязка на l-ом шаге
Определяется поправка к предыдущему приближению искомых начальных условий с помощью алгоритма МНК для линейных задач оценивания.
Уточняется предыдущее приближение вектора оценок начальных условий
Проверяется условие окончания условия последовательных приближений.
В качестве критерия завершения расчётов выступает например:
Одновременное выполнение всех неравенств, где
К
К
Если эти условия не выполняются, то мы должны перейти на решение пункта 2
Конец
Получение линеаризованной модели
Причины расхождения (не схождения) алгоритмов оценивания для получения оценок:
Неверный выбор начального приближения
Плохая обусловленность задачи оценивания
Наличие аномальных изменений
Неверные априорные данные об ошибках измерений и математической модели движения
Некорректный выбор метода расчета частных производных
Неверный выбор шага интегрирования при математическом расчете
Блок схема нелинейного алгоритма МНК оценивания
Самые большие трудности связаны с расчетом матрицы функции влияния Ф, на это рассчитывается почти все время расчетов. Матрицы Ф можно пересчитывать не каждый раз.
Точности мнк оценок для нелинейного случая
В отличии от линейных задач оценивания
математическое ожидание
и ковариационная матрица
здесь не могут быть получены. Их элементы
рассчитываются с помощью метода
статистических испытаний, что связано
с большими вычислительными затратами.
Метод наименьших модулей (мнм).
Закон распределения Лапласа.
Предположим, что относительно ошибок измерений представляемых случайной скалярной величиной h, кроме того что они случайны, аддитивны и обладают дисперсию . Результат не определён. Неопределенность может быть описана энтропией.
Задача
сводится к тому, что мы ищем точность
распределения
- ?, при которой
Ограничения:
Плотность распределения случайной величины
Заменяя интегралы на суммы и пользуясь методом неопределённых множителей Лангранжа при поиске энтропии получим решение:
Что приводит к:
Рассмотрим случай
предыдущей задачи, но при условии когда
Закон распределения случайной величины h с
Предположение о распределении ошибок измерения по закону Лапласа является более осторожным предположением, чем предположение о нормальном законе распределения во всех случаях, когда точностные характеристики неизвестны или нестабильны.
Алгоритм метода наименьших модулей.
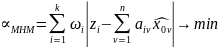
часто эта задача решается методом линейного програмирования
В общем виде алгоритм МНМ выглядит следующим образом:
Для вектора определяемых параметров задается начальное приближение
l:=0 (раньше использовал e)
Вычисляется l-ое приближение для всех весовых коэффициентов.
Где
Решается задача оценивания по МНК, находится очередное приближение
(
)
Если выполняется то завершение, если
нет то на пункт 2!!!Завершение задачи