Теплопровідність плоскої стінки при граничних умовах третього роду

Нехай плоска стінка омивається із лівої сторони рідини із t_p1 і інтенсивністю тепловіддачі α₁, з другого боку омивається рідиною із температурою t_p2 і інтенсивністю тепловіддачі α₂. Оскільки густина теплового потоку величина постійна і однакова, як з тепловіддачі з обох сторін, так і теплопровідності. Тоді густина теплового потоку від гарячої рідини до стінки буде:

q= α₁(t_p1 – t₁)

Густина теплового потоку через тверду стінку:

Густина теплового потоку від стінки до холодної рідини:

q= α₂ (t₂ – t_р2)

Перепишемо ці рівняння відносно температури:

Складемо рівняння:

або

,

де R₁ – термічний опір тепловіддачі від гарячої рідини до стінки; R₂ – термічний опір пласкої стінки; R₃ – термічний опір тепловіддачі від холодної рідини до стінки.

Позначимо

Тоді q=k(t_p1 – t_p2)=kΔt

q=kΔt або Q=kFΔt

Ці рівняння називають основними рівняннями теплопередачі.

Величину k – назвемо коефіцієнтом теплопередачі і вона показує, яка кількість теплоти передається від гарячого теплоносія до холодного через одиницю поверхні в одинцю часу при різниці температур між теплоносіями в один градус.

Q =kFΔtτ [Дж]

В теплообмінниках при прямотоці має місце наступна графічна залежність температури:

Тут за диференціальним законом. Уточнене рівняння

теплопровідності:

q=kΔt_сер. Для змінного току:

Порядок знаходження коефіцієнта тепловіддачі α

1. Встановлюємо фізичну модель взаємодії поверхні стінки з навколишнім середовищем.

2. Знаходимо відповідне критеріальне рівняння, яке описує процес тепловіддачі. Наприклад, рідина в турбулентному режимі омиває стінки. Процес тепловіддачі знаходиться за формулою:

Де l – характерний геометричний розмір, C_p – питома теплоємність при P=const, μ – коефіцієнт динамічної в’язкості, λ_р – теплопровідність рідини.

3. Розрахуємо рівняння і з критерію знайдемо коефіцієнт тепловіддачі.

;

Диференційне рівняння теплопровідності

Розглянемо фізичне тіло, де тепло передається за рахунок теплопровідності. Припускаємо:

1. тіло однорідне і ізотропні;

2. всі фізичні величини – теплопровідність, густина та інші постійні;

3. в тілі відсутні теплові джерела те стоки теплоти;

4. нехтуємо тепловою деформацією тіла.

В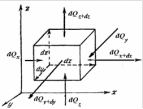 иділимо елементарний паралелепіпед об’ємом dV=dxdydz, з ребрами паралельно орієнтовні вісям паралелепіліда dx, dy, dz.

Припустимо, що тепло в такому паралелепіпеді переноситься за рахунок теплопровідності, тоді через паралелепіпед проходить певна кількість тепла. Тоді кількість теплоти, яка входить в паралелепіпед через ліву грань по координаті х буде:

dQx=qxdydzdτ

qx+dx – густина теплового потоку на площадці dF, кількість теплоти, яка проходить через ліву грань може бути представлена рядом Тейлера:

Приймемо до уваги перші два члени, нехтуючи рештою через їх малу величину:

- густина потоку через лівій грань

Тоді тепловій потік через ліву грань буде:

Різниця між кількістю тепла, що ввійшла в паралелепіпед і кількістю тепло, що вийшла із нього буде:

На вісі ox:

На вісі oy:

На вісі oz:

Приймаючи що:

Підставляючи кожне із цих значень у вирази dQ і скласти накопичення енергії у всьому об’ємі, отримаємо:

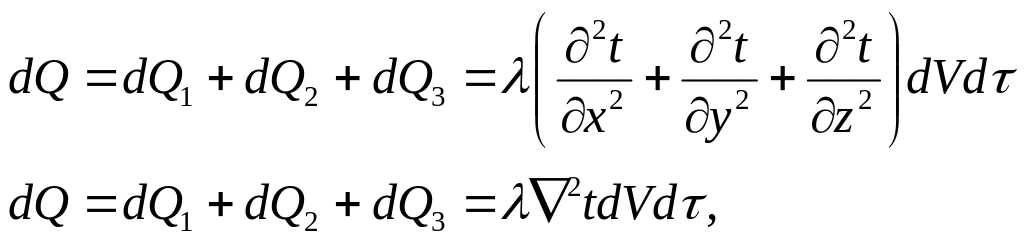
де – оператор Лапласа.

З іншого боку згідно з законом збереження енергії, кількість приросту тепло в паралелепіпеді, дорівнює зміні його ентальпії при ρ=const, тоді:

Прирівнюючи два останні вирази, складаючи і приймаючи, що λ/(ρСр)=а , ми можемо записати

Це і є диференціальне рівняння теплопровідності в нерухомому середовищі. Коефіцієнт а = λ/(ρСр) – називають коефіцієнтом температуропровідності, який характеризує тепло інерційні властивості тіла.

Інтегрування цього рівняння дає t=f(x,y,z,τ). Якщо процес стаціонарний тоді

dt/dτ = 0

Останнє рівняння – це рівняння для стаціонарного температурного поля.

Коли температурне поле стаціонарне і одномірне, тоді

dt/dy = 0 dt/dz = 0 dt/dτ=0

Останнє рівняння – це диференційне рівняння теплопровідності для одномірного стаціонарного температурного поля.