§ 1.7. Вплив періодичного збурення на частку з двома енергетичними рівнями

Це завдання займає особливе місце у квантовій електроніці, допомагаючи усвідомити особливості впливу монохроматичного електромагнітного поля на речовину з відповідною системою енергетичних рівнів. Розглянемо частку, гамільтоніан якої H° має два власні значення W_m і W_n (рівні m i n), причому W_m>W_n, тобто рівень m верхній. Відповідні хвильові функції гамільтоніан H°ψ_mo і ψ_по визначаються формулою (1.37). Припустимо, на частку діє періодичне обурення частотою ω, близькою до частоти переходу , а оператор обурення H^в [див. формулу (1.35)] запишемо у вигляді . Визначимо ймовірність знаходження частинки на рівнях m i n.

При обчисленні коефіцієнтів Ейнштейна вже вирішувалося подібне завдання в першому наближенні теорії збурень. Тут же знайдемо точне рішення. Виходимо з рівняння (1.41). Перш за все обчислимо матричні елементи оператора обурення:

(1.96)

де введено позначення .

Неважко бачити, що Н^в_Пт==(Н^в_тп)*. Будемо вважати, що діагональні матричні елементи оператора H^в дорівнюють нулю (H^в_HH=H^в_mm=0). Підставляючи явний вигляд матричних елементів оператора H^в в рівняння (1.41), одержуємо два рівняння для коефіцієнтів а_т і а_п:

(1.97)

У праві частини рівнянь (1.97) входять по два складники. Складові з показником експоненти або є швидко осцилюючими і мало впливають на рішення. Тому ними можна знехтувати. Тоді рівняння (1.97) придбають вигляд:

(1.98)

де введено позначення .

Помноживши праву і ліву частини першого рівняння (1.98) на ехр (iбt) і продиференціювавши отриману рівність, отримаємо

.

Використовуючи друге рівняння (1.98), після приведення подібних членів отримаємо

(1.99)

Знайдемо рішення рівняння (1.99) у вигляді

a_m=A exp αt. (1.100)

Після підстановки (1.100) в (1.99) отримуємо для показника експоненти α рівняння

з корінням

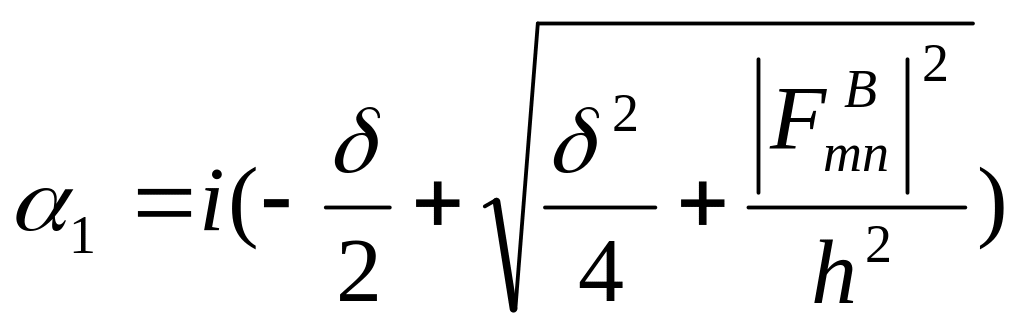
Увівши позначення отримаємо два рішення виду (1.100), що відповідають двом коріння a₁ і а₂:

(1.101)

Загальне рішення рівняння (1.99) являє собою лінійну комбінацію рішень виду (1.101), тобто

(1.102)

Коефіцієнт a_n(t) легко визначити, якщо підставити вираз (1.102), один раз продиференціювавши, в перші рівняння (1.98). Тоді

(1.103)

Задамося наступними початковими умовами: a_m(0)=0, a_n(0) = 1, тобто в початковий момент часу частинка знаходиться на нижньому рівні. Підстановка початкових умов у вирази (1.102), (1.103) дає A₁+A₂=0;

Звідси

і коефіцієнти a_m(t) і а_n(t) приймають остаточний вигляд:

. (1.104)

Імовірність знаходження частинки на рівні т визначається квадратом модуля коефіцієнта a_m(t), тобто

(1.105)

У межі дуже слабкого збурення точне рішення (1.105) переходить в рішення (1.58). Дійсно, підставами у формулу (1.105) явний вигляд величини ':

.

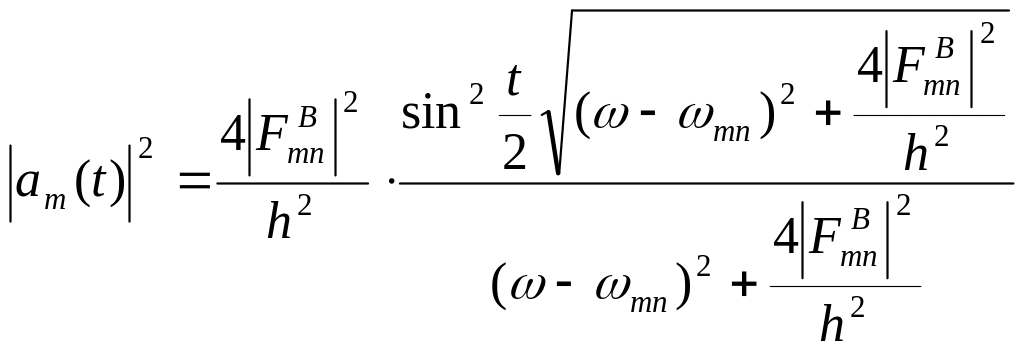Якщо , то ,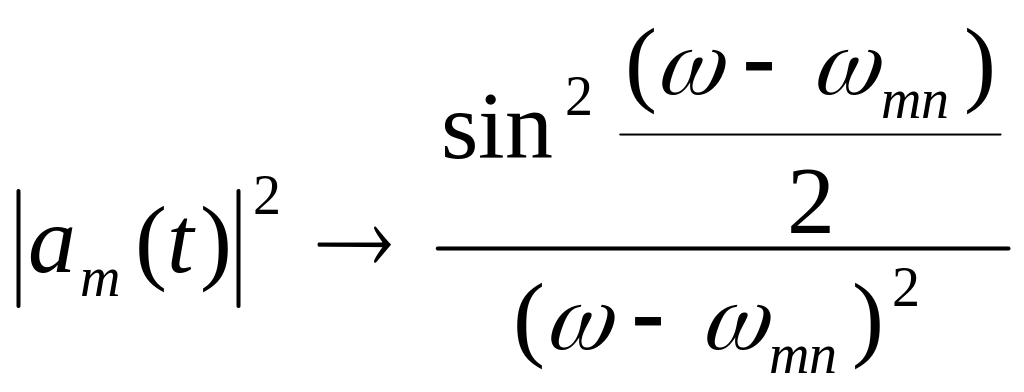

тобто до виду (1.58).

Пояснимо тепер фізичний зміст формули (1.105). Видно, що ймовірність знаходження частинки на верхньому рівні є періодична функція часу з частотою 2 '. Те ж саме можна сказати і про знаходження частинки на нижньому рівні, тому що повна ймовірність знаходження частинки в системі (тобто на верхньому та нижньому рівнях) дорівнює одиниці.

Звідси випливає, що під впливом періодичного збурення частка переходить з нижнього рівня на верхній, і навпаки. Частота (2 '), з якою відбувається такий перехід при точному резонанс (б=0), дорівнює , тобто визначається величиною матричного елементу оператора збурення. Для випадку електро-дипольного взаємодії, дуже поширеного у квантовій електроніці , де d - оператор електричного дипольного моменту, а Е - амплітуда високочастотного електричного поля, і частота .

Таким чином, при взаємодії однієї і тієї ж системи рівнів з електромагнітним полем частота перекидання частки полем з рівня на рівень пропорційна амплітуді високочастотного електричного поля і може змінюватися в дуже широких межах. Сама ймовірність знаходження частинки на верхньому рівні при точному резонансі змінюється від 0 (cos2 t = l, в цей момент частка знаходиться на нижньому рівні п, як і в початковий момент) до .

Якщо ж частота періодичного збурення не збігається з відстанню по частоті між рівнями m і n, то змінюється як частота перекидання часток з рівня на рівень, так і ймовірність знаходження частинки на верхньому рівні. Ця ймовірність завжди менше одиниці і падає зі зростанням б.