1.2.2 Үздіксіз кездейсоқ шама ықтималдықтарының үлестірім функциясы және тығыздығы

х әрбір мәні үшін Х кездейсоқ шамасының х-тен кіші мәнді қабылдау ықтималдығын анықтайтын F(x) функциясын үздіксіз кездейсоқ шама (ҮКШ) ықтималдықтарының үлестірім функциясы деп атайды, яғни

.

Кейде «үлестірім функциясы» терминінің «интегралдық үлестірім функциясы» терминін пайдаланады.

Үлестірім функциясының келесі қасиеттері бар:

1) үлестірім функциясының мәндері [0;1] кесіндісіне тиесілі ( );

2) үлестірім функциясы – х₂ > х₁ болғанда кемімейтін функция ;

3) егер Х кездейсоқ шамасының барлық мүмкін мәндері [a;b] интервалына тиесілі болса, онда болғанда және болғанда .

Үлестірім функциясынан бірінші туындыны ҮКШ ықтималдықтары үлестірімінің тығыздығы (дифференциалдық функциясы) деп атайды.

F(х) үлестірім функциясы және f (х) тығыздығы арасындағы байланыс мына ара қатыстармен өрнектеледі

; . (1.26)

X үздіксіз кездейсоқ шамасының [a; b] кесіндісіне тиесілі мәнді қабылдауының ықтималдығы мынаған тең

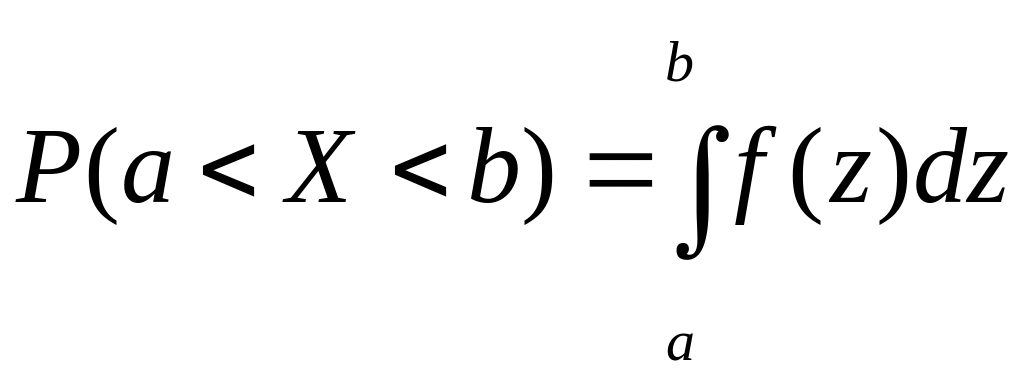. (1.27)

Үлестірім тығыздығының қасиеттері:

1) үлестірім тығыздығы – теріс емес функция: f(x) > 0;

2) - ∞-тен + ∞-ке дейінгі шектегі үлестірім тығыздығынан меншікті емес интеграл бірге тең

. (1.28)

Үлестірім тығыздығы графигін үлестірім қисығы деп атайды.

1.12-мысал. Х үздіксіз кездейсоқ шамасы үлестірім функциясымен берілген. Үлестірім тығыздығын табу керек.

;

1.1-сурет – Үлестірім функциясының және тығыздығының графиктері (1.12-мысал)

Анықтау керек:

а) Х-тің 0,2-ден кіші мәнді қабылдау ықтималдығы.

;

б) ;

в) . Берілген оқиғаның (б) оқиғасына қарама-қайшы екендігін байқаймыз.

1.13-мысал. Үздіксіз кездейсоқ шама Х үлестірім функциясымен берілген. Үлестірім тығыздығын табу керек.

;

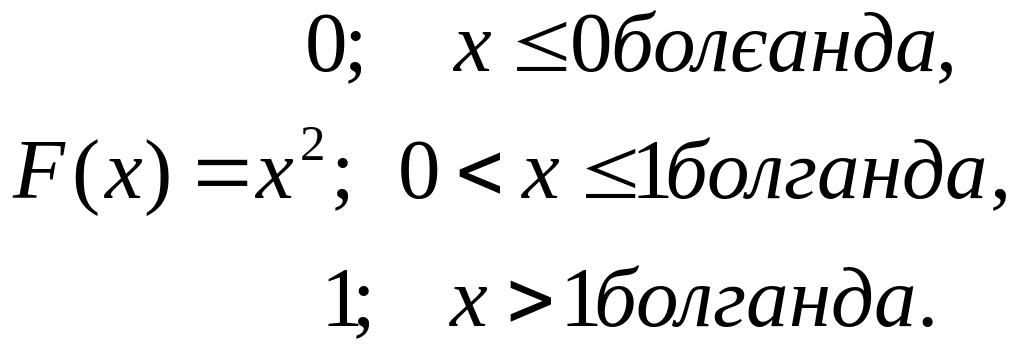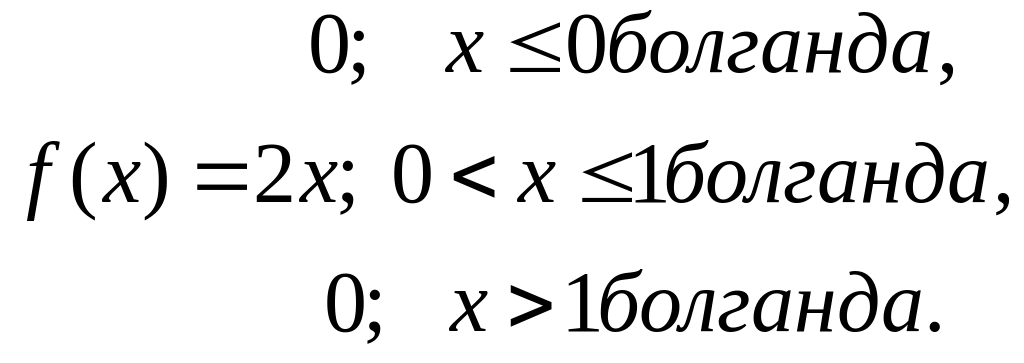
1.2-сурет – Үлестірім функциясының және тығыздығының графиктері (1.13-мысал)

4 рет сынау нәтижесінде Х шамасының (0,25; 0,75) интервалына тиесілі мәнді тура үш рет қабылдауының ықтималдығын есептеу керек.

а) Жеке сынауды қарастырамыз. Х-тің (0,25; 0,75) интервалына түсу ықтималдығы мынаған тең

; немесе

.

б) Бернулли формуласы бойынша

.

1.14-мысал. Х үздіксіз емес кездейсоқ шамасы үлестірім функциясымен берілген. Үлестірім тығыздығын табу керек.

;

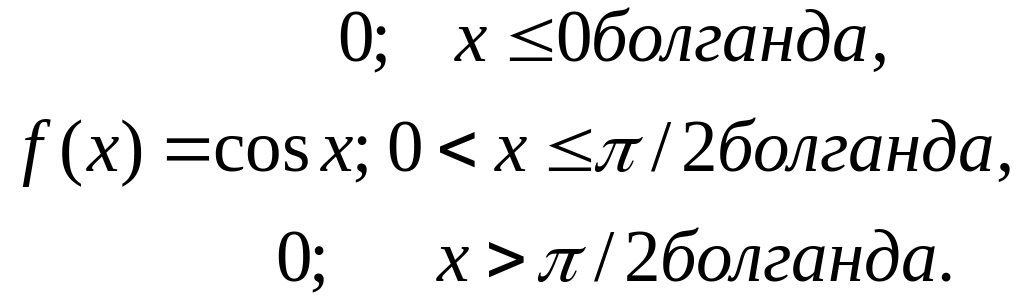
1.3-сурет – Үлестірім функциясының және тығыздығының графиктері (1.14-мысал)

1.2.3 Үздіксіз кездейсоқ шамалардың сандық сипаттамалары

Дискрет шамалардың сандық сипаттамаларының анықтамалары үздіксіз шамаларға таралады. X үздіксіз кездейсоқ шамасы f(x) үлестірім тығыздығымен берілген болсын. X барлық мүмкін мәндері [а,b] кесіндісіне тиесілі деп жорамалдайық.

Анықталған интегралды

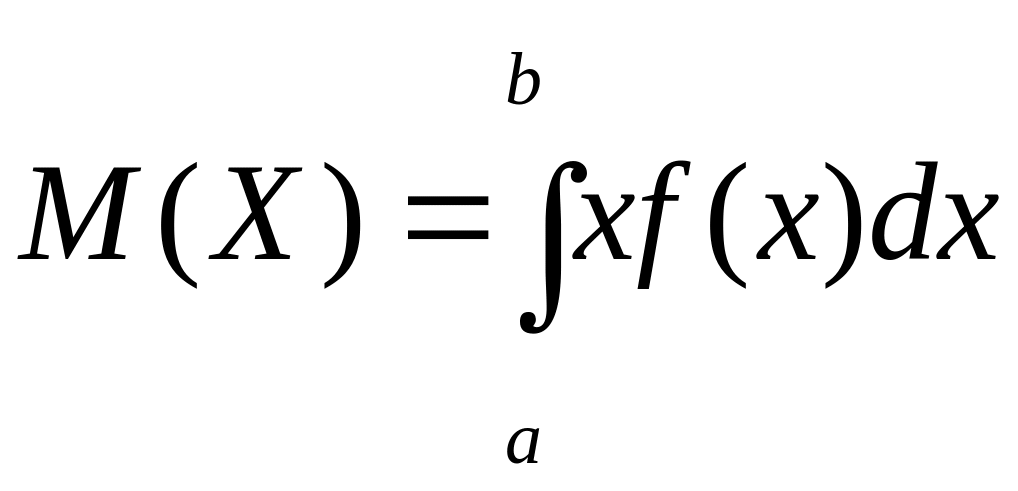, (1.29)

және егер кездейсоқ шама [-∞; ∞] кесіндісінде анықталған болса, меншікті емес интегралды

, (1.30)

мүмкін мәндері [а; b] кесіндісіне тиесілі X үздіксіз кездейсоқ шамасының математикалық үміті деп атайды.

Дискрет шаманың дисперсиясымен ұқсастығы бойынша үздіксіз шаманың дисперсиясы да анықталады.

Оның ауытқу квадратының математикалық үмітін үздіксіз кездейсоқ шаманың дисперсиясы деп атайды. [а; b] кесіндісінде анықталған кездейсоқ шама үшін дисперсия мына интегралды

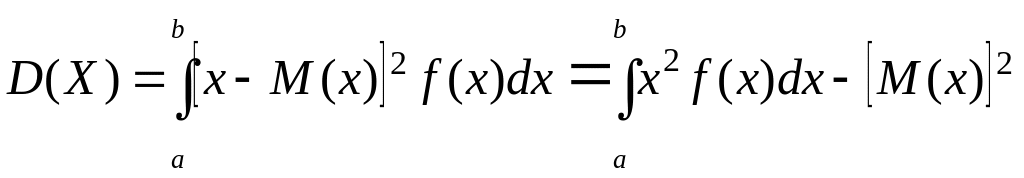, (1.31)

және егер кездейсоқ шама [-∞; ∞] кесіндісінде анықталса, меншікті емес интегралды білдіреді

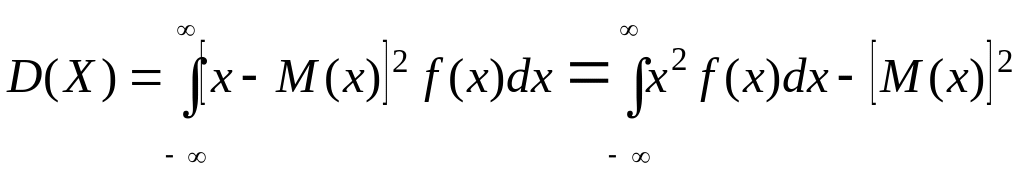. (1.32)

Үздіксіз кездейсоқ шаманың орташа квадраттық ауытқуы дискрет шама сияқты мына теңдікпен анықталады

.

Математикалық үміттің және дискрет шамалар дисперсиясының қасиеттері үздіксіз шамалар үшін де сақталады.

1.15-мысал. 1.13 және 1.14-мысалдардың деректері бойынша кездейсоқ шамалардың сандық сипаттамаларын есептеп шығару керек:

а) ; б)

1) Математикалық үміт

а) ;

б) .

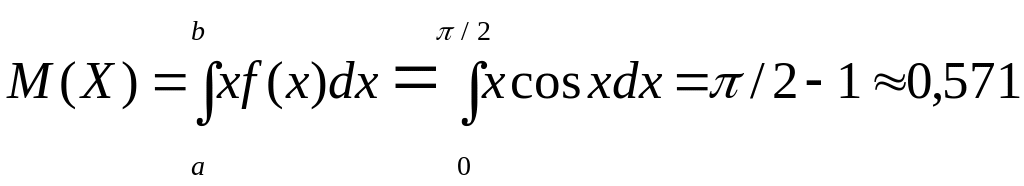2) Дисперсия және СКО

а) ;

.

б) ;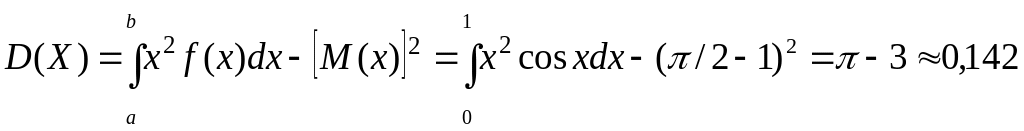

.

Математикалық үміт мәнінің f(x) тығыздығымен және х осімен шектелген фигураның ауырлық центрінің абсциссасына сәйкес келетінін атап өтеміз.