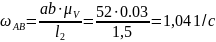- •Вариант № 60 Задача с-1
- •Задача с-2
- •Задача с-3
- •1. Рассмотрим равновесие узла h, в котором сходятся стержни 1, 2. 3.
- •2. Рассмотрим равновесие узла м.
- •Задача к-1
- •2. Скорость и ускорение точки
- •3. Касательное и нормальное ускорение точки при
- •4. Радиус кривизны траектории при
- •Задача к-2
- •Построение плана скоростей начнем с ведущего звена ав.
- •2. Построим план ускорений механизма.
- •Задача д-1
- •Рассмотри движение груза на участке ав, считая его материальной точкой.
- •Рассмотрим теперь движение груза на участке bc.
2. Скорость и ускорение точки

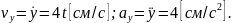
Заметим,
что
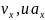 не зависят от переменной t.
не зависят от переменной t.
При
 получаем
получаем

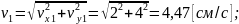
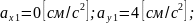

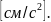
3. Касательное и нормальное ускорение точки при
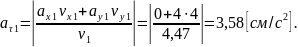
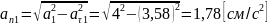
4. Радиус кривизны траектории при

Ответ: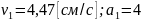
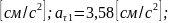
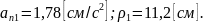
Задача
К 1б.
Точка
движется по дуге окружности радиуса R
= 2 м
по
закону
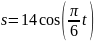 ,
(s
— в метрах, t
—
в секундах), где s
= АM
— расстояние точки от некоторого начала
A,
измеряемое вдоль дуги окружности.
Определить скорость и ускорение точки
в момент времени t=1
с. Изобразить на рисунке векторы
,
(s
— в метрах, t
—
в секундах), где s
= АM
— расстояние точки от некоторого начала
A,
измеряемое вдоль дуги окружности.
Определить скорость и ускорение точки
в момент времени t=1
с. Изобразить на рисунке векторы
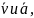 считая что точка в этот момент находится
в положении M,
а положительное направление отсчета s
– от А к М
считая что точка в этот момент находится
в положении M,
а положительное направление отсчета s
– от А к М
Исходные данные для расчета:
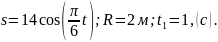
Решение:
Определяем скорость точки
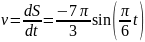
при
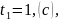 получим
получим
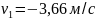
Ускорение находим по его нормальной и касательной составляющим:
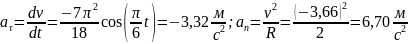
Тогда полное ускорение точки при будет равно
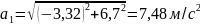


 M
M 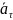
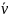
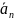 A
A
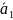
Рис. К.1.6.б)
Изобразим
на рис. К.1.6.б) векторы
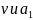 ,
учитывая знаки
,
учитывая знаки
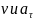 ,
и считая положительным направление от
А
к М.
,
и считая положительным направление от
А
к М.
Задача к-2
Плоский механизм состоит из стержней 1, 2, 3,4 и ползуна В (рис. К3.6.), соединенных друг с другом и с неподвижными опорами О1, О2 шарнирами; точка D находится в середине стержня АВ. Длины стержней равны соответственно:
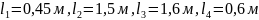 .
Положение механизма определяется
углами
.
Положение механизма определяется
углами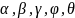 .
.
Заданные
угловую скорость и угловое ускорение
считать направленными против часовой
стрелки, а заданные скорость
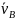 н
ускорение
н
ускорение
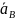 — от
точки В
к b
(рис.
К3.5).
На рис.К.3.6 показана схема механизма.
— от
точки В
к b
(рис.
К3.5).
На рис.К.3.6 показана схема механизма.
Исходные
данные для расчета: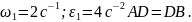
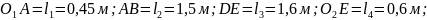
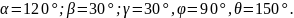
Найти: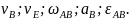
Решение:

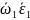

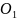
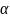
 2
A 1
2
A 1
D
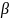

B
 3
3
b
4 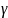
E
Рис. К 3.6
Построение плана скоростей начнем с ведущего звена ав.
Найдем скорость точки А по формуле:
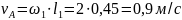 .
.
Выбираем на плоскости произвольную точку р — полюс плана скоростей, которая является началом отсчета (т.е. в этой точке все скорости равны нулю.), и откладываем на ней вектор pa, перпендикулярно звену АО1. Точка a на плане скоростей соответствует точке A на плане механизма.
Длина отрезка рa изображает на плане скоростей вектор VA скорости точки A и выбирается произвольно, исходя из того, что весь план скоростей займет на чертеже площадь около 100 см2.
Примем длину вектора ра равной 30 мм-ч, тогда масштабный коэффициент плана скоростей будет:

и покажет, сколько метров в секунду действительной величины скорости содержится в одном миллиметре отрезка чертежа.
Известно
направление и траектория движения точки
A
со скоростью в данный момент времени
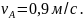 Рассмотрим группу Ассура, образованную
звеньями 1
и 2.
Шатун 2
совершает плоскопараллельное движение,
ползун прямолинейное поступательное
движение (частный случай плоскопараллельного
движения). Найдем скорость движения
точки B,
которая одновременно принадлежит звену
АВ и звену
Рассмотрим группу Ассура, образованную
звеньями 1
и 2.
Шатун 2
совершает плоскопараллельное движение,
ползун прямолинейное поступательное
движение (частный случай плоскопараллельного
движения). Найдем скорость движения
точки B,
которая одновременно принадлежит звену
АВ и звену
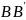 .
Где точка
.
Где точка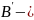 точка, связанная с неподвижной направляющей
ползуна (стойкой). Составим систему
двух векторных уравнений, которая
связывает искомую скорость точки со
скоростями других характерных точек
точка, связанная с неподвижной направляющей
ползуна (стойкой). Составим систему
двух векторных уравнений, которая
связывает искомую скорость точки со
скоростями других характерных точек
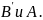 Так как звено 2
совершает плоскопараллельное движение,
то скорость точки B
будет равна скорости точки A,
сложенной векторно со скоростью точки
А (относительная скорость обозначается
Так как звено 2
совершает плоскопараллельное движение,
то скорость точки B
будет равна скорости точки A,
сложенной векторно со скоростью точки
А (относительная скорость обозначается
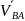 )
)
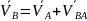
Здесь двойной индекс BA показывает, что скорость является относительной и точка B движется относительно точки A. По другому скорость точки В находится так:
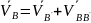
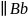
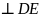
b
d
p e
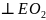
a
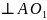
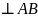
Рис. 3.6.1 План скоростей
Таким образом, получим систему двух векторных уравнений:
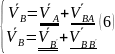
Под вектором ставим две черты, если он известен по величине и по линии действия и одну величину, если известен только один из этих параметров.
В
этой системе уравнений известны по
модулю и линии действия векторы скоростей
точек A
и
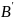 (скорость
точки
равна
нулю, т.к. она связана со стойкой). Векторы
относительных скоростей неизвестны
по величине, но известны их линии
действия. Вектор
перпендикулярен
к звену АВ,
а
вектор
(скорость
точки
равна
нулю, т.к. она связана со стойкой). Векторы
относительных скоростей неизвестны
по величине, но известны их линии
действия. Вектор
перпендикулярен
к звену АВ,
а
вектор
 параллелен
прямой Вb
(рис. К3.8).
Векторы
абсолютных скоростей выходят из полюса,
а векторы относительных скоростей
не проходят через полюс р.
параллелен
прямой Вb
(рис. К3.8).
Векторы
абсолютных скоростей выходят из полюса,
а векторы относительных скоростей
не проходят через полюс р.
Система (6) может быть решена графическим методом, путем построения плана скоростей.
В
соответствии с первым уравнением системы
(6) на плане скоростей через точку a
проводим
прямую, перпендикулярную к звену АВ.
Это линия действия вектора
,
а в соответствии со вторым уравнением
через полюс p
(точка
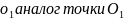 на плане механизма – совпадает с полюсом
р)
проводим на плане прямую параллельную
прямой Bb
на плане механизма.
Это линия действия вектора
.
Точка пересечения этих двух прямых
определит точку
на плане механизма – совпадает с полюсом
р)
проводим на плане прямую параллельную
прямой Bb
на плане механизма.
Это линия действия вектора
.
Точка пересечения этих двух прямых
определит точку
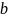 ,
которая является концом вектора
,
которая является концом вектора
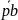 ,
изображающего на плане вектор скорости
,
изображающего на плане вектор скорости
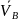 .
Вектор
.
Вектор
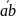 на плане механизма изображает вектор
относительной скорости точки A
относительно точки B:
.
Вектор абсолютной скорости
совпадает с вектором относительной
скорости
.
На плане скоростей они изображаются
вектором
.
на плане механизма изображает вектор
относительной скорости точки A
относительно точки B:
.
Вектор абсолютной скорости
совпадает с вектором относительной
скорости
.
На плане скоростей они изображаются
вектором
.
Для
определения действительной величины
любого из полученных векторов
достаточно умножить соответствующий
отрезок плана скоростей на масштаб
плана скоростей
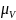 .
Результат
записываем с точностью до трёх значащих
цифр. Из плана скоростей определим
длину отрезка pb,
который
позволит найти скорость точки B
.
Результат
записываем с точностью до трёх значащих
цифр. Из плана скоростей определим
длину отрезка pb,
который
позволит найти скорость точки B
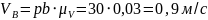
Чтобы
определить скорость точки D,
которая
принадлежит звену ADB,
воспользуемся
свойством подобия и сначала найдем
величину вектора
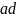 .
Величину
ad
находим
из пропорции:
.
Величину
ad
находим
из пропорции:
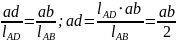
следовательно, точка d лежит на середине отрезка ab. Соединяя точки p и d, получим искомый вектор pd. Измерим его и найдем скорость точки D
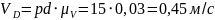
Рассмотрим следующую группу Ассура – звено 3 и звено 4.
Система уравнений для точки Е будет иметь следующий вид:
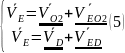
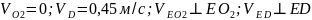 .
Производим соответствующие построения
и находим на плане точку e.
Замеряем отрезок pe
и умножаем на масштабный коэффициент:
.
Производим соответствующие построения
и находим на плане точку e.
Замеряем отрезок pe
и умножаем на масштабный коэффициент:
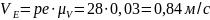
Чтобы
найти угловую скорость
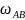 ,
надо скорость точки B
относительно точки A
(т.е. скорость
,
надо скорость точки B
относительно точки A
(т.е. скорость
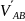 )
разделить на длину звена AB:
)
разделить на длину звена AB: