25.2. Імпульс сили та його проекції на координатні осі

Спостереження вказують на те, що одна і та сама сила може різним тілам надати однакові кінематичні стани, але при цьому час дії сили на ці тіла повинен бути різним.

Дію сили на матеріальну точку за деякий проміжок часу можна визначити імпульсом сили.

Імпульс сили характеризує передачу матеріальній точці механічного руху за деякий проміжок часу з боку інших тіл, з якими взаємодіє дана матеріальна точка.

Якщо сила, що діє на матеріальну точку, є сталою за модулем і напрямом, то імпульс сили за проміжок часу дорівнює добутку вектора сили на проміжок часу τ і має напрям цієї сили, тобто:

, (25.7)

де

.

Якщо сила, що діє на точку, змінюється з плином часу за модулем чи напрямом, то проміжок часу розбивають на елементарні проміжки часу, вважаючи при цьому силу сталою, а потім обчислюють інтегральну суму елементарних імпульсів

; (25.8)

. (25.9)

Проектуючи обидві частини (23.9) на координатні осі маємо:

; ; . (25.10)

Отже, проекція імпульсу сили на вісь дорівнює імпульсу проекції сили на цю вісь . Модуль і напрям імпульсу сили визначається за формулами:

;

; ; . (25.11)

25.3. Теорема про зміну кількості руху матеріальної точки.

Кількістю руху або векторною мірою механічного руху матеріальної точки називається вектор , який дорівнює добутку маси точки на вектор її швидкості і має напрям вектора швидкості

. (25.12)

З апишемо основне рівняння руху матеріальної точки і перетворимо його ліву частину

.

Отже,

. (25.13)

В правій частині цього рівняння силу можна розглядати як окрему силу, або як рівнодійну кількох сил, що діють на матеріальну точку (рис. 23.2).

Рівняння (25.13) визначає теорему про зміну кількості руху матеріальної точки в диференціальній формі:

Векторна похідна за часом від кількості руху матеріальної точки дорінює вектору сили, яка діє на матеріальну точку.

Розділимо змінні в рівнянні (25.13) і зінтегруємо обидві його частини, після цього отримаємо:

або

. (25.14)

Рівняння (25.14) визначає теорему про зміну кількості руху матеріальної точки в інтегральній (скінченій) формі:

Зміна кількості руху матеріальної точки за деякий проміжок часу дорівнює імпульсу сили, що діє на точку, за той самий проміжок часу.

Проектуємо обидві частини рівняння (23.14) на координатні осі:

; ; . (25.15)

Отже, зміна проекції кількості руху матеріальної точки за деякий проміжок часу дорівнює проекції імпульсу сили, що діє на точку, за той самий проміжок часу і на ту саму вісь.

25.4 Теорема про зміну головного вектора кількості руху механічної системи

Головним вектором кількості руху механічної системи називається векторна величина, що дорівнює геометричній сумі кількості рухів матеріальних точок, які складають механічну систему:

.

Отже, головний вектор кількості руху механічної системи дорівнює добутку маси системи на вектор швидкості її центра мас і має напрям цього вектора:

. (25.16)

Розглянемо механічну систему, яка складається з n матеріальних точок. Нехай на точки цїєї системи діють зовнішні ( ) та внутрішні ( ) сили.

Тоді теорема про зміну кількості руху для j-ої точки цієї системи в диференціальній формі матиме вигляд:

. (25.17)

Запишемо таких рівнянь стільки, скільки точок має дана система та підсумуємо їх:

. (25.18)

Перетворимо ліву частину рівняння (23.18):

. (25.19)

Підставивши отримане значення (23.18) в (23.19) та враховуючи, що , остаточно маємо:

. (25.20)

Рівняння (25.20) визначає теорему про зміну головного вектора кількості руху механічної системи в диференціальній формі.

Векторна похідна за часом від головного вектора кількості руху механічної системи дорівнює геометричній сумі всіх зовнішніх сил, прикладених до точок системи, або головному вектору всіх зовнішніх сил, які діють на точки механічної системи.

Проектуємо обидві частини рівняння (23.20) на осі декартової системи координат:

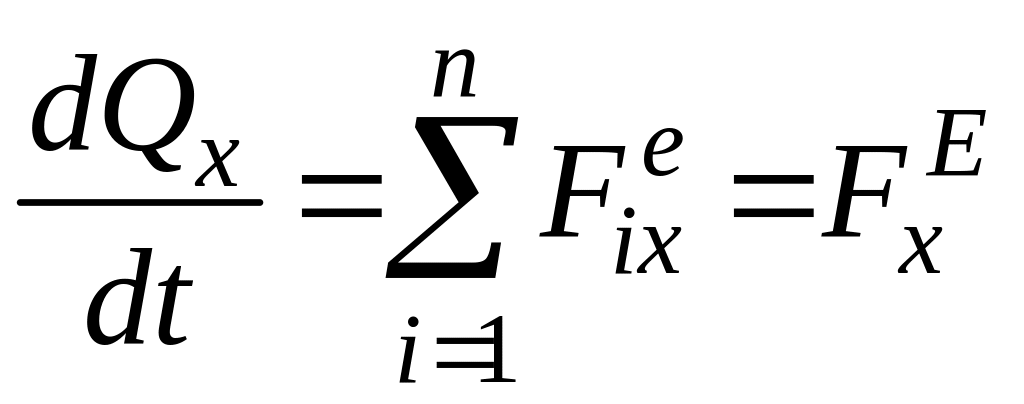; ; . (25.21)

Отже, перша похідна за часом від проекції головного вектора кількості руху механічної системи на будь-яку вісь дорівнює алгебраїчній сумі проекцій зовнішніх сил, які діють на точки механічної системи, або проекції головного вектора зовнішніх сил на ту саму вісь.

Для отримання теореми про зміну кількості руху механічної системи в інтегральній (скінченій) формі використаємо рівняння (25.21).

Домножимо обидві його частини на і зінтегруємо в межах від до :

.

Після інтегрування остаточно дістанемо:

. (25.22)

Рівняння (25.22) визначає теорему про зміну головного вектора кількості руху механічної системи:

Зміна головного вектора кількості руху механічної системи за деякий проміжок часу дорівнює геометричній сумі імпульсів зовнішніх сил, які діють на точки механічної системи за той самий проміжок часу, або повному імпульсу головного вектора зовнішніх сил.

Спроектувавши обидві частини рівняння (25.22) на координатні осі дістанемо:

; ; . (25.23)

Отже, зміна проекції головного вектора кількості руху механічної системи на будь яку вісь за деякий проміжок часу дорівнює алгебраїчній сумі проекцій імпульсів зовнішніх сил, що діють на точки механічної системи за той самий проміжок часу і на ту саму вісь, або проекції повного імпульсу головного вектора зовнішніх сил на цю вісь.

Наслідки з теореми:

1. Внутрішні сили безпосередньо не впливають на зміну головного вектора кількості руху механічної системи.

2. Якщо головний вектор усіх зовнішніх сил, які діють на точки механічної системи, дорівнює нулю, то головний вектор кількості руху цієї системи є векторною сталою величиною ; .

3. Якщо проекція головного вектора зовнішніх сил, що діють на точки механічної системи, на будь-яку вісь дорівнює нулю, то проекція головного вектора кількості руху механічної системи на ту саму вісь є сталою величиною( ; .

Другий і третій наслідки називаються законами збереження кількості руху механічної системи.