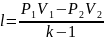3 Термодинамические процессы

Термодинамическим процессом называется процесс изменения состояния рабочего тела, связанный с изменением его параметров. В технической термо­динамике рассматриваются следующие термодинамические процессы:

• изохорный процесс - при постоянном объеме (V=const);

• изобарный процесс - при постоянном давлении (P=const);

• изотермический процесс - при постоянной температуре (T=const);

• адиабатный процесс - без теплообмена с внешней средой (dq=0);

• политропный процесс (PV ⁿ = const, -∞ < n < +∞).

В таблице 1 приведены основные математические соотношения для указанных термодинамических процессов.

Таблица 1

Процесс	Уравнение процесса	Соотношение между параметрами	Механическая работа	Теплота
Изохорный	V=const		l=0
Изобарный	Р=const
Изотермический	Т=const РV=const			q=l
Адиабатный	dq=0 РVк=const			q=const
Политропный	РVn=const

Изохорный процесс

Задачи:

1. В закрытом сосуде емкостью у = 0,6 м³ содержится воздух при давлении р_л = 0,5 МПа и температуре f = 29 °С. При охлаждении сосуда воздух, находящийся в нем, теряет 105 кДж. Определить давление и температуру воз­духа в конце процесса охлаждения, принимая теплоемкость воздуха величиной постоянной 0,722 кДж/кг К.

Решение:

Из уравнения состояния находим

кг,

Количество теплоты, отводимой от воздуха в процессе, определяется уравнением:

Q = M C_vm(t₂-t₁)

откуда

-40,7 + 20 =-20,7 °С,

Из соотношения параметров в изохорном процессе имеем

МПа.

2. Двигатель внутреннего сгорания работает с подводом теплоты в процессе V=const. Состояние рабочей смеси перед зажиганием: P₁ = 1,2 МПа и t₁= 400 °С. Определить температуру в конце процесса сгорания, если давление продуктов сгорания Р₂ = 4 МПа.

Решение:

; К; °С

Изобарный процесс

Задачи:

1. В цилиндре с объемом 400 л находится воздух при давлении Р₁ -0,5МПа и t_л =400 °С. От воздуха отнимается теплота в процессе при по­стоянном давлении благодаря чему в конце процесса устанавливается тем­пература t₂ =0 °С. Определить количество потерянной теплоты, конечный объем, изменение внутренней энергии и работу сжатия, считая теплоемкость величиной постоянной. Расчет провести по формуле, связанной с объемом и массой газа.

Решение:

а) Количество потерянной теплоты (в процессе охлаждения) определяем по формуле

Q_р=V_HC'_Pm(t₂-t₁)

где V_H - объем воздуха, приведенный к нормальным условиям, л;

С’_Pm - объемная теплоемкость, кДж/м³.

т³

C'_Pm = 1,33 кДж/(м³нк)

тогда

Q_р = 0,8  1,33(0 - 400) = -425 кДж

б) Это количество теплоты можно определить по формуле

Q_P=MC_Pm(t₂-t₁),

где М - масса воздуха, кг;

С_Рт - массовая теплоемкость, кДж/(кг К)_.

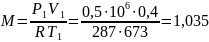кг, С_Рт =1,03 кДж/(кгК)

Q_р = 1,035-1,03(0-400) = -425 кДж

Конечный объём

, м³

Изменение внутренней энергии определяется по формуле

u₂-U₁=V_HС’_v т(t₂-t₁),

Работа, затраченная на сжатие, определяется по формуле

L = P(V₂ – V₁) = 0,5  10⁶  (0,162 - 0,4) = -118,9 кДж,

2. Определить тепловую мощность электрического калорифера, предназначен­ного для нагревания потока воздуха от температуры г, t₁= -20 °С до t₁ = 20° С; производительность вентилятора 3600 м³/ч. Теплоемкость воздуха считать постоянной. Барометрическое давление Р_о = 750 мм рт. ст.

Решение:

Массовый расход воздуха через калорифер

кг/c

Мощность калорифера

Q=MC_Pm(t₂-t₁),

Изотермический процесс

Задачи:

1. Один килограмм воздуха при температуре t₁ =30° С и начальном давлении Р, =10,1 МПа сжимается изотермически до конечного давления Р₂ = 1 МПа. Определить конечный объем, затрачиваемую работу и количество теплоты, отводимой от газа.

Решение:

Начальный объем воздуха можно определить из уравнения состояния

м³/кг

Конечный объем определяется из уравнения

Р₁V₁=P₂V₂; м³/кг

Работа, затрачиваемая на сжатие 1 кг воздуха, получается из уравнения

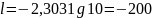; кДж/кг

кДж/кг.

2. При изотермическом сжатии 5 м³ азота отводится 600 кДж тепла. Опреде­лить работу сжатия, конечное давление Р₂ и объем V₂ газа, если начальное давление Р₁ =0,08 МПа.

Решение:

В изотермическом процессе затрачиваемая работа на сжатие рабочего тела равняется отведенному теплу L = Q = 600 кДж.

Из выражения ,

Находим Р₂ = 0,36 МПа,

Конечный объем к ; м³_.

Адиабатный процесс

Задачи:

1. В процессе адиабатного сжатия в цилиндре дизеля температура воздуха повышается до величины, равной температуре воспламенения топлива, объем при этом уменьшается в 14 раз. Определить конечные температуры и давления воздуха, если Р₁ = 0,1МПа и t₁= 100 °С.

Решение:

Конечная температура определяется по формуле

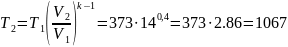K.

Конечное давление находится из уравнения

МПа.

2. Один килограмм воздуха с начальной температурой t₁=20°С и давлением Р, = 0,6 МПа расширяется адиабатно до давления Р₂ = 0,1 МПа. Определить параметры состояния в конце процесса расширения, работу процесса и изменение внутренней энергии газа.

Решение:

Температура в конце процесса

K.

Удельный объем воздуха в конце процесса

м³/кг

Работа в адиабатном процессе

кДж/кг

политропньш процесс

Задачи:

1. Один килограмм воздуха при P₁ =0,5 МПа и t, =111 °С расширяется политропно до давления Р₂ =0,1 МПа. Определить конечное состояние воздуха, изменение внутренней энергии, количество подведенной теплоты и полученную работу, если показатель политропы n=1,2.

Решение:

Начальный объем воздуха определяется по уравнению

м³/кг

Конечный объем воздуха определяется по уравнению

м³/кг

Конечная температура определяется из уравнения состояния

К

Величина работы определяется по формуле

кДж/кг

Изменение внутренней энергии

кДж/кг

Количество теплоты, сообщенной воздуху, определяется из уравнения

кДж/кг

2. 1,5 кг воздуха сжимается политропно от Р₁ =0,9 МПа и t₁ =18 °с до Р₂ =1МПа, температура при этом повышается до t₂ = 185 °С. Определить показатель политропы, конечный объем, затраченную работу и количество отведенной теплоты.

Решение:

Из уравнения

Конечный объем

м³

Затраченная работа

кДж/кг

Количество отведенной теплоты

кДж/кг