Методические указания к контрольной работе № 1

Ниже приведены образцы решения отдельных задач.

1. Бригада рабочих подрядилась выкопать колодец. За выемку первого метра было выплачено 625 рублей, за каждый следующий расценки увеличивались на 20% по сравнению с предыдущим. Известно, что бригада получила 4651 руб. Какой глубины колодец выкопала бригада?

Решение

Так как каждый последующий метр оплачивался на 20% дороже, то за второй метр было выплачено 625 + 6250,2 = 6251,2 руб., за третий – 6251,21,2 = 625(1,2)² руб., за п-ый метр оплачивали 625(1,2)^{п – 1} руб. По условию задачи, выкопав п метров, бригада получила 4651 руб., то есть имеем уравнение:

625 + 6251,2 + 625(1,2)² + … + 625(1,2)^{п – 1} = 4651

В левой части этого равенства стоит сумма п членов геометрической прогрессии, которая может быть вычислена по формуле , где q знаменатель прогрессии, b₁ – ее первый член. У нас q = 1,2, b₁ = 625, поэтому

откуда . Так как 2,48832 = (1,2)⁵ , то п = 5. Таким образом, бригада выкопала колодец глубиной 5 метров.

2. Найти область определения функции y = ln(2 – x – x²) + х.

Решение

Логарифмическая функция определена только для положительных значений аргумента, поэтому должно выполняться неравенство 2 –х – х² > 0. Для решения этого неравенства найдем корни квадратного трехчлена и воспользуемся формулой ax² + bx + c = a(x – x₁)(x – x₂).

2 –х – х² = 0  D = 1+8 = 9  х₁ = 1; х₂ = –2.

Неравенство принимает вид: –(х – 1)(х + 2) > 0  (х – 1)(х + 2) < 0. Применяя метод интервалов, получим

то есть область определения для первого слагаемого – интервал (–2; 1).

Корень четной степени можно извлекать только из неотрицательных чисел, поэтому второе слагаемое дает х  0, то есть – полуинтервал 0; +).

Область определения всей функции – это пересечение полученных множеств: (–2; 1) 0; +) = 0; 1).

3. Методом сдвигов и деформаций построить график функции у = (х + 2)² + 1.

Решение

Г рафик этой функции получается из графика функции у = х² параллельным переносом на 2 единицы влево и на одну единицу вверх (рис.1):

Рис.1. Построение графика функции у = (х + 2)² + 1.

4. Вычислить пределы:

а) ; б) .

Решение

а) Так как при подстановке х = 4 получается неопределенность вида , разложим числитель на множители.

.

б) Так как при х   числитель и знаменатель дроби являются бесконечно большими функциями, разделим числитель и знаменатель на х². Заметим также, что функция вида const/xⁿ при х   является бесконечно малой. Поэтому .

5. Найти производную функции (y^/_x) и вычислить ее значение при x = 0:

а) ; б) (1 – у)х + у² = 4.

Решение

а) Пользуясь формулами дифференцирования, имеем

.

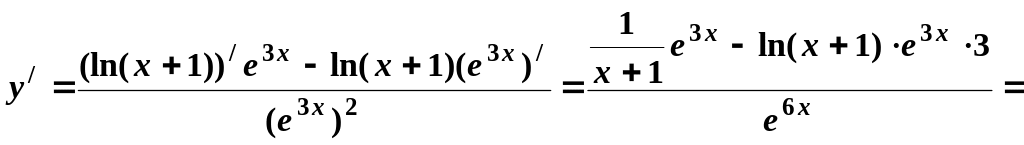
Вычислим значение производной в точке x = 0:

.

б) Здесь функция задана неявно, поэтому сначала продифференцируем обе части равенства по переменной х, учитывая, что у = у(х):

у ^/х + 1 – у + 2уу ^/ = 0. Из полученного уравнения найдем y ^/_x:

у ^/ (2у – х) = у – 1  .

Чтобы найти y ^/(0), найдем сначала значение функции при x = 0. Подставив 0 в исходное равенство, получим у² = 4  у(0) = +2.

Итак, при у = 2 ;

при у = – 2 .

6. Исследовать функцию у = 0,3х⁵ – х³ – 12х + 1 и построить ее график.

Решение

1. Область определения данной функции – все действительные числа: xR .

2. Точек разрыва нет.

3. f(–x) = 0,3(–х⁵) – (–х³) – 12(–х) + 1 = – 0,3х⁵ + х³ + 12х + 1.

Так как f(–x)  f(x) ; f(–x)  – f(x) , то функция не является ни четной, ни нечетной.

4. Функция не периодическая

5. При х = 0 у = 1, точно найти координаты точек пересечения графика функции с осью Ох (при у = 0) невозможно.

6. Уравнение наклонной асимптоты имеет вид y = kx+b ,

где ; .

Для горизонтальной асимптоты k = 0 .

Вычислим . Следовательно, наклонных и горизонтальных асимптот нет.

7. у ^/ = 1,5х⁴ – 3х² – 12 .

у ^/ = 0 при х₁ = 2, х₂ = – 2.

8. у ^// = 6х³ – 6х .

у ^// = 0 при х₃ = 0, х₄ = 1, х₅ = – 1.

9. Сводная таблица:

   х	(–;–2)	–2	(–2; –1)	–1	(–1;0)	0	(0;1)	1	(1;2)	2	(2;+ )
   у /	+	0	–	–	–	–	–	–	–	0	+
   у //	–	–	–	0	+	0	–	0	+	+	+
   у		23,4		13,7		1		-11,7		-21,4
   вы­вод	возраст., выпукл	max	убыв., выпукл.	точка перег	убыв., вогнут	т. пер	убыв. выпук	т. перег	убыв. вогн.	min	возраст вогнут

10. Г рафик (рис.2).

Рис.2. График функции

7. Найти и изобразить область определения функции:

.

Решение

Так как логарифмическая функция определена только для положительных значений аргумента, а знаменатель дроби должен быть отличен от нуля, то областью определения функции являются те точки, координаты которых удовлетворяют системе неравенств:

х + у + 1 > 0

х² + у²  0

Выражение х² + у² = 0 определяет на плоскости точку О(0; 0). Таким образом, второе неравенство указывает, что эта точка должна быть исключена из области определения функции. Первому неравенству удовлетворяет множество точек плоскости, лежащих выше прямой у = –1 – х, без самой этой прямой (рис.3).

Рис.3. Область определения функции задачи 7

8. Найти , если z = y³ lnx.

Решение

Чтобы найти , вычислим частную производную функции по переменной х, а затем полученное выражение продифференцируем по у:

z ^/_x = y³/x; z ^//_xy = 3y²/x.

9. Найти стационарные точки и исследовать на экстремум функцию

z = x³ – 6xy + y³ .

Решение

Найдем стационарные точки функции.

z ^/_x = 3x² – 6 y ; z ^/_y = 3у² – 6x ;

3x² – 6y = 0

3у² – 6x = 0 .

Чтобы решить полученную систему, выразим из первого уравнения у и подставим во второе уравнение. Получим у = х²/2 ;

(х²/2)² – 2х = 0  х⁴ – 8х = 0  х(х³ – 8) = 0 ,

откуда х₁ = 0, х₂ = 2 ; у₁ = х₁²/2 = 0 , у₂ = х₂²/2 = 2 .

Таким образом, нашли две стационарные точки М₁(0; 0) и М₂(2; 2).

Найдем вторые частные производные: z ^//_xx = 6х ; z ^//_xу = – 6 ; z ^//_уу = 6у .

Исследуем точку М₁(0; 0):

А = z ^//_xx (М₁) = 0 ; В = z ^//_xу (М₁) = – 6 ; С = z ^//_уу (М₁) = 0 .

 = AC – B² = – 36 < 0 , следовательно, в точке М₁ функция не имеет экстремума.

Исследуем точку М₂(2; 2):

А = z ^//_xx (М₂) = 12 ; В = z ^//_xу (М₂) = – 6 ; С = z ^//_уу (М₂) = 12 .

 = AC – B² = 112 > 0 , следовательно, в точке М₂ функция имеет экстремум, а так как А = 12 > 0, то М₂ – точка минимума.

Подсчитаем минимальное значение функции:

z_min = z(2;2) = 2³ + 2³ – 622 = – 8 .

10. Найти корни уравнения методом половинного деления. Результат округлить до двух знаков после запятой.

Решение. Перепишем уравнение в виде . Построим на одном чертеже графики левой и правой частей уравнения, то есть, графики функций и . Корни уравнения соответствуют точкам пересечения графиков. Из рисунка видно, что исходное уравнение имеет два корня. Определим по графику отрезки, каждый из которых содержит единственный корень. Это отрезки [–1;0] и [0;1].

Д ля уточнения корней используем метод деления пополам. Делим исходный отрезок [a; b] пополам точкой c = (a + b)/2, из двух получившихся отрезков [a; c] и [c; b] выбираем тот, на концах которого функция принимает значения разных знаков. Выполнение такого условия для непрерывной функции f(x) гарантирует существование корня на этом отрезке.

При каждом делении пополам размер отрезка, содержащего корень, а следовательно, и погрешность решения уменьшается вдвое. Вычисления следует прекратить, когда длина отрезка станет меньше заданной погрешности (в нашем случае меньше 0,01).

Выполним один шаг описанного алгоритма для отрезка [0; 1]. Вычислим значения функции в точках 0, 0,5 и 1. Получим

f(0) = –0,54;

f(0,5)= –0,75;

f(1) = 0,46.

Функция f(x) имеет разные знаки на концах отрезка [0,5; 1], поэтому выбираем его для второго шага. На втором шаге получаем

f(0,5)= –0,75;

f(0,75) = –0,32;

f(1) = 0,46.

Аналогично, для третьего шага выбираем отрезок [0,75; 1] и продолжаем вычисления. Выполнив необходимое число шагов, получим, что корень уравнения находится на отрезке [0,859; 0,867], длина которого уже меньше заданной погрешности определения корня. В качестве значения корня возьмем середину этого отрезка – значение 0,863 и округлим полученный результат до двух знаков после запятой. Получим, что корень равен 0,86.

Аналогично отыскивается второй корень.

Ответ. x₁ = 0,86; x₂ = –0,25.