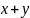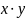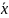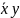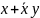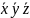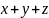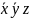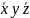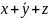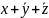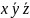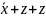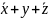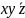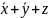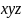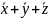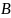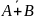Bramki logiczne, od lewej: not, nand I nor zbudowane na tranzystorach npn

Zajmijmy się najpierw rysunkiem pierwszym od lewej. Jeżeli napięcie baza-emiter czyli V_in = 0 (wartość bitu wejścia jest 0) to, jak wynika z poprzedniej analizy, natężenie prądu kolektor-emiter będzie małe (bliskie zera). Z prawa Ohma (U = IR) wynika że wtedy różnica potencjałów V_cc – V_out też będzie mała, natomiast różnica potencjałów między kolektorem a emiterem będzie duża (bliska V_cc). To oznacza, że wartość bitu na wyjściu wynosi 1.

Jeżeli napięcie baza-emiter czyli V_in> 0 (wartość bitu wejścia jest 1), to natężenie prądu kolektor-emiter będzie duże. Z prawa Ohma (U = IR) wynika że wtedy różnica potencjałów V_cc – V_out też będzie duża (bliska V_cc), natomiast różnica potencjałów między kolektorem a emiterem będzie mała (bliska 0). To oznacza, że wartość bitu na wyjściu wynosi 0. Tabela wartości urządzenia jest taka jak bramki logicznej NOT.

Jeżeli dwa tranzystory połączymy szeregowo (kolektor do emitera) to napięcie na wyjściu jest funkcją dwóch napięć V_in1 oraz V_in2. Jeżeli przynajmniej jedno z nich ma wartość 0 to natężenie prądu kolektor-emiter w obydwu tranzystorach będzie małe a zatem wartość napięcia V_out będzie bliska napięciu V_cc czyli duża. Więc tak połączone tranzystory realizują bramkę logiczną NAND.

Podobnym rozumowaniem można znaleźć tablicę wartości obwodu równolegle połączonych tranzystorów.

Obecnie rolę przełącznika pełnią tranzystory. Dokładniej dwa typy tranzystorów polowych N-type Field EffectTransistor (NFET)) , który otwiera przełącznik po otrzymaniu sygnału o wysokim napięciu a zamyka gdy sygnał ma niskie napięcie, tranzystor drugiego typu(P-type Field EffectTransistor (PFET)) reaguje odwrotnie. Tak połączone tranzystory realizują bramkę logiczną NOR. Procesory współczesne zawierają tranzystory obydwu typów, technologia taka nosi nazwę Complementary Metal Oxide Semiconductor (CMOS).

Przykład

Znaleźć tabele wartości funkcji NAND i NOR.

Algebra Boola

Zaprojektowanie sieci przełączników, która wykonywałaby złożone polecenia, np. obliczała sumę iloczynów wielu par liczb 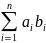, metodą prób i błędów jest prawdopodobnie możliwe ale czasochłonne. Projektowanie sieci przełączników (sieć przełączników to nic innego jak pewien procesor) wykonujących określone zadanie wymaga użycie odpowiedniego narzędzia matematycznego. Jest nim algebra wielkości dwuwartościowych stworzona przez Irlandczyka, Georga Boola, w 18 wieku nazywana dzisiaj algebrą Boola. Tworzy ją (jak każdą teorię matematyczną) zbiór aksjomatów i twierdzeń. Teraz sformułujemy niektóre z nich, inne wtedy gdy będą potrzebne. Wszystkie zmienne algebry Boola mogą przyjmować tylko dwie wartości 0 i 1. Trzy podstawowe operacja (działania) logiczne jakie można na nich wykonywać zdefiniowane są poniższymi tabelami wartości.

Dodawanie logiczne (OR) Mnożenie logiczne (AND) Zaprzeczenie (NOT)

0	0	0
1	0	1
0	1	1
1	1	1

0	0	0
1	0	0
0	1	0
1	1	1

0	1
1	0

Przy okazji widać, że istnieją dwa sposoby zapisywania operacji logicznych: OR ≡ ‘+’, AND ≡ ‘∙’ (zazwyczaj kropkę się pomija). Z tabel można wywnioskować dwa twierdzenia De Morgana: 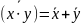, oraz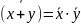 . (sprawdzić)

Funkcje logiczne są wyrażeniami algebraicznymi zmiennych binarnych, symboli operacji logicznych, nawiasów i znaku równości. Dla określonych wartości zmiennych funkcja logiczna ma wartość 1 lub 0. Istotnymi właściwościami operacji logicznych jest przemienność (OR i AND są przemienne, to zna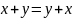czy np. ), oraz łączność (OR i AND są łączne, to znaczy np. 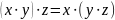). Operacje NOR i NAND zdefiniowane jako zaprzeczenie OR i zaprzeczenie AND nie są łączne, to znaczy

, podobnie .

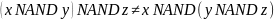Przykład

Zbadamy właściwości funkcji:

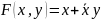
Funkcja nie jest skomplikowana, więc najprościej jest utworzyć tabelę wartości funkcji. Ostatnia kolumna podaje dodatkowo wartości funkcji OR tych samych zmiennych:

x	y
0	0	0	0	0
0	1	1	1	1
1	0	0	1	1
1	1	0	1	1

Powyższy przykład ilustruje znane z zwyczajnej algebry przypadki gdy to samo wyrażenie algebraiczne można zapisać na kilka sposobów.

Projektowanie obwodów logicznych

Konstrukcja (budowa) funkcji, które ma być modelem jakiegoś urządzenia logicznego często prowadzi do skomplikowanego wyrażenie algebraicznego. Urządzenie jest siecią bramek (które są zbudowane z tranzystorów) połączonych elektrycznie zbudowaną na podstawie modelu matematycznego w postaci funkcji logicznej. Analiza modelu urządzenia na jego podstawie staje się łatwiejsza gdy model ma prostą strukturę algebraiczną. Również budowa urządzenia na podstawie prostego modelu (o minimalnej liczbie bramek i połączeń) jest łatwiejsza i oczywiście tańsza . Im bardziej złożone operacje ma wykonywać procesor tym ważniejsze jest poszukiwanie najprostszego modelu matematycznego procesora w postaci funkcji logicznej. Jedna z ważniejszych technik projektowania procesorów zwana syntezą polega na budowie a następnie sprowadzaniu do najprostszej postaci funkcji logicznej tablicy wartości procesora.

Wykorzystuje się w niej wyrażenia Sum-Of-Products (SOP) i Product-Of-Sums (POS). Te dwa wyrażenia łatwo odczytać z tabeli wartości projektowanej struktury logicznej. Przy ich pomocy można zbudować analityczną postać funkcji logicznej struktury. Zmienna logiczna może wystąpić w postaci normalnej x lub komplementarnej . Dwie zmienne x i y połączone operacją AND mogą wystąpić w czterech kombinacjach xy, 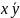, , 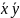. Każde z tych wyrażeń nazywa się iloczynem standardowym (minterm). Dla n zmiennych tego typu wyrażeń jest 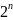. Wartość logiczną każdego z nich można znaleźć za pomocą tabeli operacji AND. Podobny zbiór wyrażeń tworzy zbiór n zmiennych powiązanych operacją OR. Każde z nich nazywa się sumą standardową. Na podstawie twierdzeń De Morgana zaprzeczenie iloczynu daje sumę wartości zaprzeczonych . Poniższa tabela podaje wszystkie iloczyny standardowe i sumy standardowe trzech zmiennych

x	y	z	iloczyn	oznaczenie	suma	oznaczenie
0	0	0		m0		M0
0	0	1		m1		M1
0	1	0		m2		M3
0	1	1		m3		M3
1	0	0		m4		M4
1	0	1		m5		M5
1	1	0		m6		M6
1	1	1		m7		M7

Bardzo przydatne w poszukiwaniu funkcji logicznej opisanej tabelą wartości jest twierdzenie:

Dowolną funkcję logiczną o znanej tabeli wartości można przedstawić w postaci wyrażenia algebraicznego o postaci sumy iloczynów dla każdej kombinacji zmiennych o wartości logicznej 1. Zmiennymi mogą również być dowolne funkcje logiczne.

Przykład

Znaleźć postać funkcji trzech zmiennych logicznych o własnościach zadanych tabelą wartości.

A	B	C	F(A,B,C)
0	0	0	0
1	0	0	1
0	1	0	0
1	1	0	1
0	0	1	0
1	0	1	1
0	1	1	0
1	1	1	1

Wartość logiczną 1 mają cztery iloczyny. Ich suma (SOP) zawiera cztery iloczyny standardowe przedstawione w poprzedniej tabeli

.

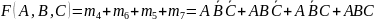Pozostałe iloczyny standardowe mają wartość 0. Powyższą funkcję można uprościć, korzystając z różnych tożsamości logicznych, np.

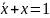
Wystarczy spojrzeć na tabelę, aby stwierdzić, że jest to prawda. Uproszczenie w tym wypadku jest istotne.

Istnieje druga możliwość budowy funkcji o zadanej tabeli. Rozpoczynamy od sumy (maxterm) każdej kombinacji zmiennych o wartości logicznej 0. Zaprzeczając powyższą sumę tworzymy nową funkcję. Na podstawie twierdzenia De Morgana ta nowa funkcja ma postać iloczynu zaprzeczonych zmiennych. Możemy więc sformułować drugą regułę budowania funkcji logicznej na podstawie tabeli wartości. Należy utworzyć sumy standardowe każdej kombinacji zmiennych mającej wartość 0 i utworzyć iloczyn logiczny tych sum.

Funkcje logiczne (funkcje Boola) utworzone z sumy iloczynów lub iloczynu sum mają postać kanoniczą.

Przykład

Znaleźć postać funkcji o trzech zmiennych logicznych o własnościach zadanych tabelą wartości.

A	B	C	F(A,B,C)
0	0	0	0
1	0	0	1
0	1	0	0
1	1	0	1
0	0	1	0
1	0	1	0
0	1	1	1
1	1	1	1

A. Za pomocą iloczynów standardowych

Jest ich cztery 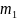, , , 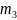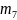. Poszukiwana funkcja SOP ma postać .

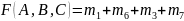Upraszczamy funkcję korzystając z tautologii , ), .

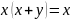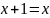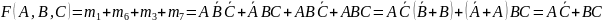
Ta funkcja ma tablicę identyczną z powyżej podaną.

B. Za pomocą sum standardowych

Jest ich cztery 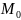, , 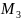, 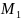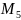. Poszukiwana funkcja POS ma postać

. Upraszczamy funkcję

.

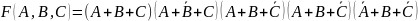
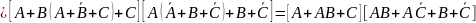
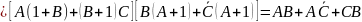Funkcję można jeszcze uprościć zauważając, że we wszystkich wierszach tabeli zawierających sumy standardowe iloczyn logiczny AB = 0, wobec tego

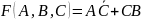tak jak poprzednio.

Podsumowanie

Algebra Boola jest narzędziem matematycznym maszyn cyfrowych

-zmienne mają tylko dwie wartości (0 lub1)

-elementarne funkcje to AND, OR i NOT, są zdefiniowane za pomocą tabel wartości

-bardziej złożone funkcje można zbudować z funkcji elementarnych (lub tabel wartości)

-twierdzenia de Morgana pozwalają przekształcić wyrażenia logiczne na inne, równoważne ale

zbudowane z innych funkcji elementarnych

Bramki logiczne (Logic Gates)

Przełączniki i przewody całkowicie wystarczają do projektowania struktur (kości) logicznych mających wykonać określone zadania. Tak zaprojektowane struktury zazwyczaj wykonują zadanie najszybciej jak to możliwe. Jednak w wypadku złożonych zadań projektowanie z użyciem przełączników jest żmudne i czasochłonne. Podobna sytuacja ma miejsce podczas tworzenia programów komputerowych, program napisany w języku maszynowym ma wiele zalet jednakże zazwyczaj piszemy programy w językach wyższego rzędu. Projektowanie struktury logicznej procesorów można uprościć posługując się metodą powszechnie stosowaną w tworzeniu programów komputerowych. Przygotowuje się coś w rodzaju klocków (zbiór wbudowanych funkcji), tutaj będą nimi układy logiczne złożone z wielu przełączników. Klockami w tym wypadku są bramki logiczne, które otrzymują kilka sygnałów logicznych i przekształcają je w jeden sygnał logiczny. Dowolną bramkę można zbudować za pomocą zbioru kilku prostych bramek. Zazwyczaj tego niewielkiego zbioru należą bramki realizujące operacje logiczne AND, OR, operacje komplementarne do nich, to znaczy zaprzeczenia NAND, NOR oraz NOT. Poniżej znajdują się tabele wartości czterech bramek, w kolumnach A i B znajdują się wartości logiczne dwóch sygnałów wejściowych a w trzeciej wartość logiczna sygnału wyjściowego.

AND			NAND
		AB
0	0	0	0	0	1
1	0	0	1	0	1
0	1	0	0	1	1
1	1	1	1	1	0
NOR			OR
					A+B
0	0	1	0	0	0
1	0	0	1	0	1
0	1	0	0	1	1
1	1	0	1	1	1

Za pomocą tych czterech operacji logicznych oraz funkcji NOT można przedstawić wszystkie, dowolnie złożone funkcje logiczne.

Podobnie jak to jest w wielu dziedzinach technicznych pożyteczne jest reprezentowanie abstrakcyjnych pojęć za pomocą symboli graficznych. W poniższych tabelach znajdują sie kompletne informacje łącznie z symbolami graficznymi o podstawowych funkcjach logicznych. W tych tabelach zaprzeczenie wartości logicznej x jest oznaczone przez x’, aby stosować nasze, dotychczas używane oznaczenia trzeba zastąpić .

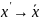Podstawowe bramki

Bardziej złożone bramki

Właściwości dwóch ostatnich bramek można zapisać poręczniej: gdy liczba jedynek na wejściu jest nieparzysta, funkcja XOR ma wartość 1 ('prawda') a Exclusive-NOR ma wartość 0 ('fałsz').

Przykład

W samochodzie światło ostrzegawcze ma się zapalać gdy drzwi są otwarte lub pasy nie są zapięte. Zaprojektować odpowiedni układ logiczny sterujący światłem.

x	drzwi		y	pasy		z	lampa
0	otwarte		0	niezapięte		0	nie świeci
1	zamknięte		1	zapięte		1	świeci

Pożądana tabela wartości układu logicznego

x	y	z
0	0	1
0	1	1
1	0	1
1	1	0

Porównanie z powyższymi tabelami wskazuje, że najprostszym takim układem jest bramka NAND.

Kombinacyjne i sekwencyjne obwody logiczne

Najogólniej obwody logiczne stosowane w urządzeniach cyfrowych dzielą się na dwie grupy: obwody kombinacyjne i obwody sekwencyjne. Obwód kombinacyjny zbudowany jest wyłącznie z bramek logicznych, wyjście z niego jest w każdej chwili jest jednoznacznie zdeterminowane przez aktualne dane na wejściu. Inaczej mówiąc obwód kombinacyjny wykonuje operacje określone wyłącznie przez zbiór funkcji Boola obwodu. Natomiast obwód sekwencyjny zawiera dodatkowo pamięci i wykonuje operacje określone przez zbiór funkcji Boola obwodu oraz zawartość swoich pamięci. Zatem wyjście z niego jest zdeterminowane zarówno przez dane na wejściu jak i informację w pamięci. Ponieważ zawartość pamięci jest zależna od sygnałów na wejściu w wcześniejszych chwilach to sygnał na wyjściu jest funkcją wejść w ostatniej chwili i w wielu poprzednich chwilach. Przetwarzanie informacji w obwodzie sekwencyjnym jest zatem funkcją struktury logicznej obwodu i sekwencji sygnałów na wejściu.