
- •Введение
- •2 ) Классификация наук
- •Глава 1. Теоретические основы информатики. Информация, ее виды и свойства
- •Единицы количества информации: вероятностный и объемный подходы Вероятностный подход
- •Объемный подход
- •Вопросы и задания
- •12. Задание:
- •13. Задание:
- •Глава 2. Программное обеспечение
- •Операционная система
- •Однопользовательские ос
- •Функции операционной системы
- •Примеры операционных систем
- •Вопросы и задания
- •Глава 3. Система счисления
- •Вопросы и задания
- •Глава 4. Логика и элементы математической логики
- •В) Операция "конъюнкция" – логический элемент и - умножение
- •Глава 5. Компьютерная сеть
- •Раздел I
В) Операция "конъюнкция" – логический элемент и - умножение



Схематическое обозначение
Математическое обозначение:
/ / .
можно писать, что
 B
=AB
B
=AB
Рис. 6
г) Импликация (
/
 )
)
Можно писать, что AB
эквивалент
 ,
таким образом, получим следующий схем:
,
таким образом, получим следующий схем:

Математическое обозначение: A B
Рис. 7
д) Эквивалентность ( / )
Можно писать, что AB
эквивалент


Закон логики и некоторые правила:
1 .
Отрицание отрицания:
.
Отрицание отрицания:
 *
*
2. Противоречия:
 ложь
ложь
3. Исключенного третьего:
 истина
истина
4. Двойственности логических связок «И» и «ИЛИ»
a)
 *
*
b)
 *
*
5. Доказательство от противного:

6. Основные тождества:
X 0 = 0; X 0 =X;
X 1 = X; * X 1 =1; *
X
 = 0; X
=1;
= 0; X
=1;
XX…X = X; * X X X … X = X; *
7. Конъюнктивное поглощение:
A (A B) = A.
8. Дизъюнктивное поглощение:
A (A B) =AA AB=A AB = A (1 B) = A.
9. Ассоциативность:
A (B C) = (A B) C = A B C;
A (B C) = (A B) C = A B C.
10. Коммутативность:
A B = B A;
A B = B A.
11. Дистрибутивность:
A (B C) = A B A C;
A (B C) = (A B) (A C).
Запомнить следующих высказываний:
1) «Все А есть В» означает
 ;
;
2) «Неверно, что А эквивалентно В» означает
 ;
;
3) «Неверно, что если С, то В» означает ;
;
4) «А тогда и только тогда, когда В» означает А↔В;
5) «Для А, достаточно В » означает В↔А;
6) «Для А, необходимо В» означает А→В;
7) «Если А, то В» означает А→В;
Задание №2
З
Для заполнения первую строку столбцы A B C, надо действовать таким образом:
1) заменить A,B и C соотв. значений 1, 0, и 1;
2) определить:
1 0 1
![]()
1 1
1
аполнить таблицу используя таблицы истинности.-
A
B
C
A B C
A B C


1
0
1
1
0
0
1
1
1
1
0
1
1
1
0
0
0
0
0
1
1
0

0
1
0
Задание №3
Определить номера наборов аргументов, на которых функция F равна 1

Решение: Функция F имеет всего 3 различных значения. F может принимать значение либо 1 либо 0 поэтому количество возможных аргументов = 23 = 8. Возможные значения: 0,1,2,3,4,5,6,7
Для аргумента 0, X1 = 0; X2 = 0; X3 = 0; Поставить эти значения в функции F; тогда получим следующие выражения:
 =0
=0
Для аргумента 1, X1 = 0; X2 = 0; X3 = 1;
 = 0
= 0
Для аргумента 2, X1 = 0; X2 = 1; X3 = 0;
 = 1
= 1
и так далее до 7.
Тогда получим, следующий набор аргументов : 2, 3, 5 и 7

Задание №4
Определить номера наборов аргументов, на которых функция F равна 1
F
=

Задание №5
Упростите логическое выражение
 .
Упрощенный вид должен содержать две
логические операции
.
Упрощенный вид должен содержать две
логические операции
Решение:
Знаем, что
 ,
тогда получим
,
тогда получим

 ;
;
применяем правило №11 раздела (закон логики…), чтобы раскрыть скобки. Так же использует:
X = 0; XX = X
=
=

=

=
 v
v

=
Задание №5
Упростите логическое выражение
 .
Упрощенный вид должен содержать две
логические операции
.
Упрощенный вид должен содержать две
логические операции
Решение:
Знаем, что
,
и что XY
=
 тогда
получим:
тогда
получим:
 =
(1)
=
(1)
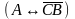 =
=
 =
= (2)
(2)
 =
= =
= =
= (3)
(3)
(1)*(2) получим:
(
)
=
 =
= =
=
=
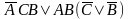 =
= =
= =
= (4)
(4)
(4)*(3) получим:
(
)
=( )
=
)
=
= ( )
= (
)
(5);
)
= (
)
(5);
Теперь можно умножать (5) на A:
A(
)= =
= =
= ;
таким образом, упрощенный вид будет
;
таким образом, упрощенный вид будет
Задание №6
Упростите логическое
выражение
 .
Упрощенный вид должен содержать две
логические операции.
.
Упрощенный вид должен содержать две
логические операции.
Задание №7
Записать логическую функцию F(A,B,C), соответствующую логической схеме представленной на рис. 8
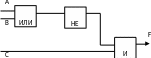

Рис. 8
Решение:
Добавим некоторые обозначений на предыдущем рисунке, тогда получим:
f1 – это функция выхода из элемента «ИЛИ» и функция входа в элемент «НЕ»;
f2 - это функция выхода из элемента «НЕ» и функция входа в элемент «И»;
f1 = A B;
f2
=
 ;
;
F = f2
C = (
)
C =
 C;
C;
F =
 ;
;
Задание №8
Записать логическую функцию F(A,B,C), соответствующую логической схеме представленной на рис. 9
Решение:
F=
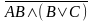 =
=
 =
=
 =
=
 ;
так как X
1 =X,то можно писать,
что F=
;
так как X
1 =X,то можно писать,
что F=
 =
= или F =
или F =


Рис. 9
Задание №9
Логическими переменными A,B, C, D, E обозначены следующие простые высказываниями: A – яблоко красное, B – яблоко вкусное, C – яблоко сладкое, D- яблоко крупное, E – яблоко твердое. Записать формулой сложное высказывание: «яблоко сладкое и твердое или невкусное».
Задание №10
Логическими переменными A,B, C, D, E обозначены следующие простые высказываниями: A – яблоко красное, B – яблоко вкусное, C – яблоко сладкое, D- яблоко крупное, E – яблоко твердое. Записать формулой сложное высказывание: «неверно, что если яблоко зеленое и крупное, то оно или твердое или кислое».
Задание №11
Истинность двух высказываний: «фирма А организует выставку, а фирма С не организует » и «если фирма В организует выставку, то фирма С тоже организует» означает организацию выставок фирма
Решение: Мы уже уверены, что фирма А организует выставку; нам говорит, что «если фирма В организует выставку, то фирма С тоже организует» - это означает, что фирма В не может организовать выставку, т.к. С не организует. Таким образом только фирма А организует выставку. Ответ: A
Решаете задачу другим способом.
Задание №12
Истинность двух высказываний: «неверно, что если корабль А вышел в море, то корабль С - нет» и «в море вышел корабль В или корабль С, но не оба вместе» означает выход в море кораблей ?
Задание №13
Школьник попросил троих друзей отгадать, какое он задумал число из набора: положительное, отрицательное, четное, нечетное, целое и дробное. Первый сказал, что если четное то оно положительное. Второй предположил, что задуманное число четное или целое и положительное. Третий был уверен, что если это число положительное, то оно нечетное. Все три оказались правы. Какое число загадал школьник?
Задание №14
Коля, Боря, Вова и Юра заняли первые 4 места в спортивных соревнованиях. На вопрос, какие они места заняли, они ответили: Коля не занял, ни первое, ни четвертое место; Боря занял второе место; Вова не был последним. Кто, какое место занял?
