Б) Признак Даламбера (Даламбер Жан Батист ле Ронд 1717-1783)

Теорема 9. Если в ряде с положительными членами u₁ + u₂ + . . .+ u_n + . . .

отношение последующего члена к предыдущему имеет предел , т.е.

, то:

1. ряд сходится при < 1;

2. ряд расходится при > 1;

3. при = 1 ответа на вопрос о сходимости или расходимости ряда теорема не дает (без доказательства).

Пример. Исследовать сходимость ряда .

Решение. ; ,

. Ряд сходится.

В) Признак Коши (Коши Август Луис 1789-1857)

Сравнение рядов с прогрессиями приводит еще к одному признаку сходимости, принадлежащему Коши.

Теорема 10. Если для ряда с положительными членами существует

, то:

1. ряд сходится при < 1;

2. ряд расходится при > 1;

3. при = 1 ответа на вопрос о сходимости остается нерешенным.

Пример . Исследовать сходимость ряда .

Решение. Для этого ряда по признаку Коши имеем

,

и поэтому заданный ряд сходится.

Пример. Исследовать сходимость ряда

Решение. Для него .

Поэтому вопрос о сходимости данного ряда признаком Коши не решается. Ясно, что этот ряд расходится, так как общий член его при n   не стремится к нулю: , при n  .

Пример. Исследовать сходимость ряда

Решение. Данный ряд как обобщенный гармонический сходится ( так как

р = 3 > 1). В то же время по признаку Коши:

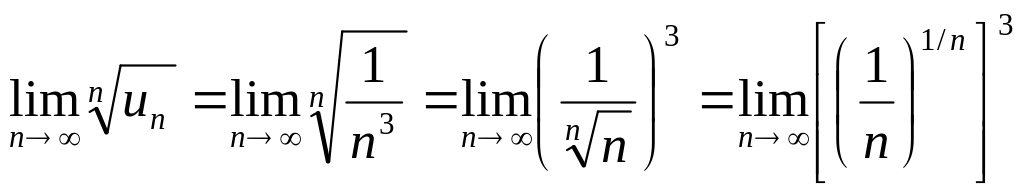= 1.

Г) Интегральный признак

Теорема 11. Пусть члены ряда u₁ + u₂ + . . . + u_n +. . . положительны и не возрастают. т.е. u₁  u₂  u₃ . . .  u_n . . ., и пусть f(x) – такая непрерывная невозрастающая функция, что f(1) = u₁, f(2) = u₂, f(3) = u₃, . . ., f(n) = u_n

Тогда справедливы следующие утверждения:

1. если несобственный интеграл , сходится, то рассматриваемый ряд сходится;

2. если указанный интеграл расходится, то расходится и рассматриваемый ряд.

Пример. .

Решение. Применим интегральный признак, положив .

Эта функция удовлетворяет всем условиям теоремы. Рассмотрим интеграл

Интеграл сходится, следовательно, и данный ряд сходится.

Замечание. Качество признака сходимости определяется его широтой, практичностью (удобством, простотой и самой возможностью применения) и чувствительностью (способностью дать ответ на вопрос о сходимости ряда). Широта признака сходимости характеризуется классом тех рядов, к которым этот признак применим. Следовательно, при изучении рядов нельзя ограничиться одним каким–либо признаком, а необходимо овладеть еще другими признаками сходимости, может быть, не столь чувствительными, но зато более практичными (удобными в обращении).

Среди рассмотренных нами признаков наиболее чувствительным является интегральный, но он не всегда практичен, т.к. его применение иногда приводит к сложным вычислениям.

Вывод: Среди изученных нами признаков наиболее чувствительным является интегральный, но его применение иногда приводит к сложным вычислениям.