8.4 Гіперболічні рівняння
Як приклад гіперболічного рівняння розглянемо математичну модель вільних коливань струни
,
(8.31)
кінці якої зафіксовані у
точках х = 0
і х = l.
У початковий момент часу кожній точці
струни придали початкове зміщення
і швидкість
.
Постійна
у рівняння (8.31) визначається вагою і
натягом струни.
Отже, процес коливань струни визначається такими початковими
при
,
(8.32)
,
при
(8.33)
і граничними
,
=0
при
(8.34)
умовами.
Задача (8.32) – (8.33) визначена
на прямокутній області
,
яка є ідентичною для задачі про
теплопровідність і тому для побудови
різницевої схеми доцільно використати
ті ж вузли, що і раніше (див. п. 8.3).
Часткові похідні другого порядку будемо апроксимувати за відомими нам формулами:
,
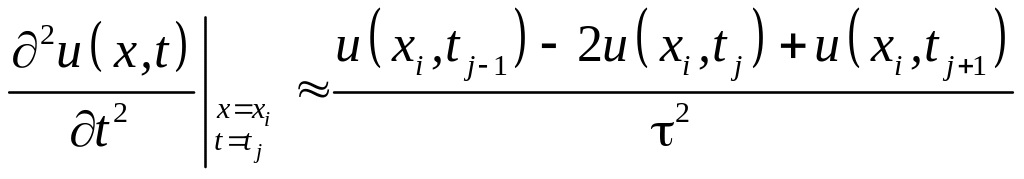(8.35)
.
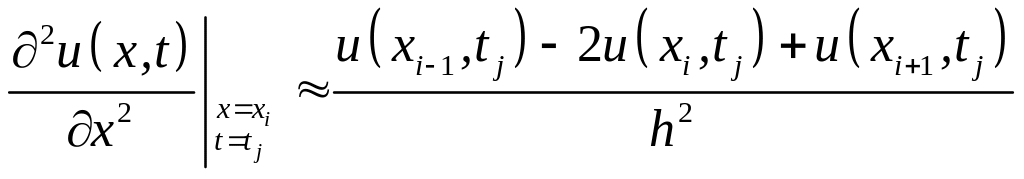(8.36)
Замінивши у (8.31) часткові
похідні
і
їх наближеннями (8.35) і (8.36), отримаємо
різницеву схему
,
яка апроксимує хвильове рівняння (8.31) на шаблоні типу «хрест» (рис. 8.4).
Якщо ввести позначення
,
то
,
(8.37)
де
,
.
Відповідним чином видозмінюється початкова (8.32)
(8.38)
і гранична (8.34)
,
,
(8.39)
умови.
Оскільки кінці струни
зафіксовані у точках
і
,
то
і
.
Початкова умова (8.33) задана у диференціальній формі, що вимагає, застосування до неї форм апроксимації. Найпростіша із них
.
Тоді відповідно з (8.33)
або
.
(8.40)
У тому випадку, коли функція має другу похідну, можна скористатися формулою Тейлора порядку два, щоб обчислити значення для другого ряду.
Оскільки
.
Відповідно до рівняння (8.31)
.
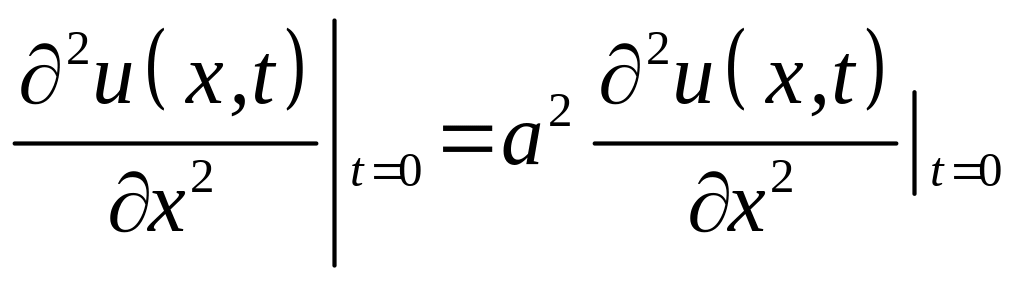
Отже,
(8.41)
Розкладемо функцію
у ряд Тейлора порядку два. Маємо
,
де
;
;
- залишковий член ряду Тейлора.
Оскільки, відповідно до
формули (8.33)
а згідно з (8.40)
то
.
(8.42)
Формулу (8.42) можна застосувати
для обчислення значень
для першого ряду. Для цього візьмемо
,
,
а функції
апроксимуємо за формулою
,
(8.43)
де
.
Оскільки
,
то формули (8.42) і (8.43) дають можливість
записати наступну формулу для дискретних
значень
:
.
Оскільки
,
то
.
Якщо врахувати, що
,
то
.
(8.44)
На відміну від формули (8.37),
яка забезпечує перший порядок точності
,
формула (8.40) має другий порядок точності
.
Доведено*,
що умова
забезпечує стійкість обчислювального
процесу за різницевою схемою (8.37).
Приклад 8.3. Задано хвильове рівняння
,
і
,
де а = 2, з граничними умовами
,
для
,
,
для
,
для
.
Знайти його розв’язок числовим
методом. Виберемо
.
Для стійкого обчислювального процесу
повинна виконуватись умова
.
Візьмемо
.
Оскільки
,
то
.
Отже, кількість точок для дискретних
значень х -
,
а для дискретних значень
.
Обчислення значень функції
у вузлах
будемо здійснювати за формулою (8.37).
Значення
для нульового ряду обчислюється за
формулою (8.38), а для першого ряду – за
(8.44).
Процедура HyperbolicEqualization знаходить наближений розв’язок хвильового рівняння (8.31) за різницевою схемою (8.37).
HyperbolicEqualization
Розв'язок хвильового рівняння (гіперболічного)
Вхід:fi(x)-визначається підпроцедурою run_fiG
psi(x)- визначається підпроцедурою run_psiG
l i tk - праві точки інтервалів [0;l] i [0;tk]
a-постійна у хвильовому рівнянні
n i m-число точок решітки [0;l] i [0;tk]
Вихід:U-матриця розв'язків
Вхідні дані
1 l=1
2 tk=0.5
3 a=2
4 m=21
5 n=21
Кроки tau і h на решітці
6 h=1/(n-1)
7 tau=tk/(m-1)
Параметри рівняння та ініціалізація U
8 gama=tau^2*a^2/h^2
9 Створити нульову матрицю U розміром nxm
Генерування значень функції u(x,t) першого і другого рядів
10 for i=2 to n-1
11 fi_1=fun_fiG(h*(i-1))
12 fi=fun_fiG(h*i)
13 fi_2=fun_fiG(h*(i-2))
14 psi_1=fun_psiG(h*(i-1))
15 U(i,1)=fi_1
16 U(i,2)=(1-gama)*fi_1+tau*psi_1+gama*(fi+fi_2)/2
17 end for
Генерування значень функції u(x,t) наступних рядків
18 for j=3 to m
19 for i=2 to n-1
20 U(i,j)=2*(1-gama)*U(i,j-1)+gama*(U(i-1,j-1)+...
21 U(i+1,j-1))-U(i,j-2)
22 end for
23 end ror
24 Побудувати графік функції у координатах x,y,U
М-файли до програми 8.3
Підпроцедура fun_fiG(x)
Функція, що задає початкові умови fi(x)
1 fi=fun_fiG(x)
2 if x<=0.5
3 then fi=x
4 else
5 fi=0.5-x
6 end if
Підпроцедура fun_psiG
Функція, що задає початкові умови fi(x)
1 psi=fun_psiG(x)
2 psi=0;
Тривимірне подання результатів обчислень показано на рис. 8.11.
Рисунок 8.11 - Графік функції