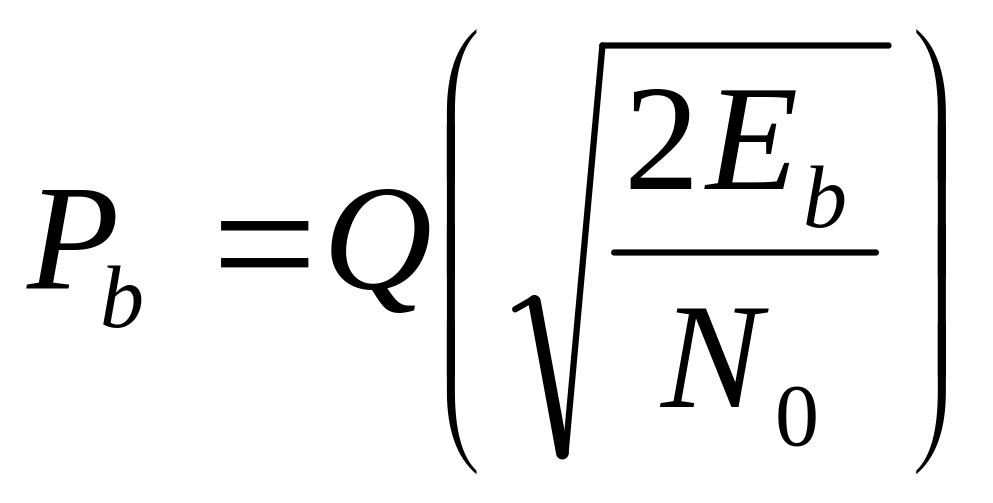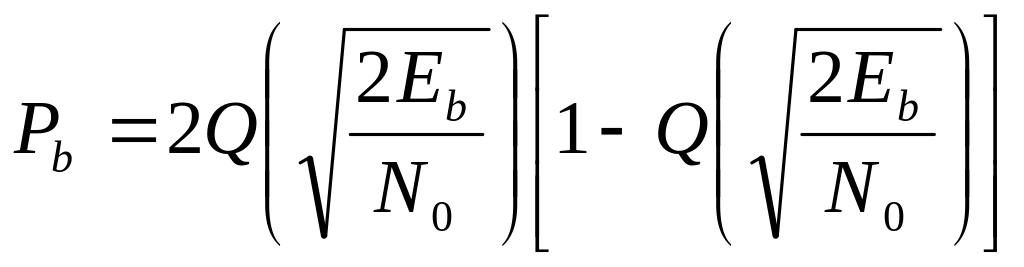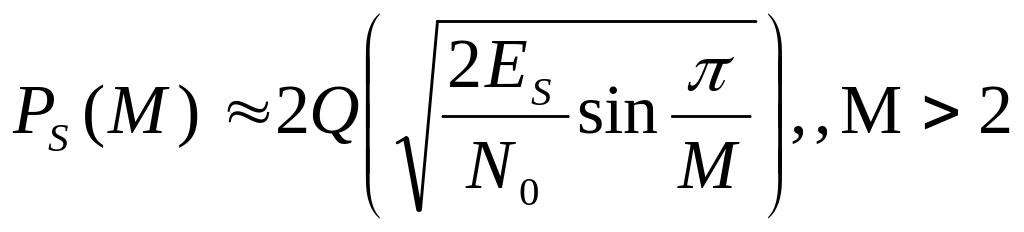- •Лабораторная работа 1 Исследование статистики ошибок в каналах связи
- •1. Краткие теоретические сведения.
- •1.2 Модель источника ошибок
- •Контрольные вопросы.
- •Лабораторная работа 2
- •1. Краткие теоретические сведения
- •1.1. Постановка задачи
- •1.2. Простые гипотезы
- •1.3. Радиолокация ( )
- •1.4. Двоичный симметричный канал
- •1.5. Вероятность ошибок при передаче сигнала по каналу с гауссовым шумом
- •2. Помехоустойчивый прием
- •2.1. Прием импульсного сигнала на фоне помех
- •2.2. Виртуальный лабораторный стенд для исследования статистических характеристик передачи импульсных сигналов по каналу с шумами
- •3. Задания к работе
- •3.1. Определение вероятности правильного приема импульса
- •3.2. Определение интегрального распределения вероятности пропуска импульса
- •3.3. Определение интегрального распределения вероятности ложного приема импульса
- •3. Контрольные вопросы
- •Лабораторная работа № 3 Изучение краевых искажений в дискретном канале
- •1. Краткие теоретические сведения.
- •Дроблением значащих интервалов называется однократное или многократное изменение значащих позиций внутри значащего интервала.
- •2. Ход выполнения работы
- •2.1. Задание
- •3. Содержание отчета
- •4. Контрольные вопросы
- •Лабораторная работа №4 Эффективное кодирование сообщений. Коды Шеннона – Фано, Хаффмена
- •1. Краткие теоретические сведения
- •1.1 Основные понятия и приемы.
- •2. Обработка полученных результатов
- •3. Контрольные вопросы
- •1. Краткие теоретические сведения
- •1.1. Оптимальный прием дискретных радиосигналов
- •1.2.Амплитудная модуляция с пассивной паузой.
- •1.3. Частотная двоичная модуляция
- •1.4. Относительная фазовая модуляция
- •2. Исследование модулированных сигналов
- •2.1. Порядок выполнения лабораторной работы
- •1. Краткие теоретические сведения
- •1.1. Виды синхронизации
- •1.2. Синхронизация приемника
- •1.3. Частотная и фазовая синхронизация
- •1.4. Символьная синхронизация
- •1.5. Разомкнутые символьные синхронизаторы
- •1.6. Замкнутые символьные синхронизаторы
- •1.7. Ошибки символьной синхронизации и вероятность символьной ошибки
- •2. Порядок выполнения работы
- •2.1. Результаты моделирования.
- •2.2. Восстановление фазы несущей
- •2.3. Результаты моделирования
- •3. Контрольные вопросы
- •Лабораторная работа № 7
- •Корректирующие коды Хемминга.
- •Моделирование кодов Хемминга в среде Матлаб
- •Ход выполнения работы.
- •4. Содержание отчета
- •1. Краткие теоретические сведения
- •1.1. Представление сверточного кода порождающими многочленами
- •1.2. Порождающая матрица сверточного кода
- •1.3. Кодовое дерево сверточного кода и решетчатая диаграмма
- •1.4. Свободное расстояние. Спектр
- •1.5. Катастрофические кодеры
- •2. Методы декодирования сверточных кодов
- •2.1. Метод порогового декодирования
- •2.2. Метод последовательного декодирования
- •2.3. Метод декодирования по алгоритму Витерби
- •2.3.1. Декодирование в случае отсутствия ошибок при приеме
- •2.3.2. Декодирование в случае наличия ошибок при приеме.
- •2.3.3. Схемное построение декодера Витерби
- •3. Моделирование сверточных кодов в среде Матлаб
- •4. Порядок выполнения работы
- •4. Литература
1.4. Двоичный симметричный канал
Двоичный симметричный канал (ДСК) – базовая модель двоичного канала связи. Передаваемые нули и единицы кодируются противоположными по знаку сигналами (передача с активной паузой). В синхронном канале сигналы могут появляться в заданные (тактовые) моменты времени. Проверяются гипотезы
:
![]() ,
,
:
![]() .
.
В теоретическом плане этот случай мало отличается от предыдущего: по-прежнему применяется согласованная фильтрация с уравнением (1), статистика
![]()
распределена по нормальному закону с дисперсией (4) и противоположными по знаку математическими ожиданиями (рис. 3):
![]() ,
.
,
.

Рис. 3. Плотности распределения статистики
В ДСК нули и единицы равновероятны (передаются одинаково часто), информационная нагрузка на них одинакова, поэтому критический уровень обеспечивает одинаковую вероятность ошибок декодера первого и второго рода (ложной тревоги и пропуска сигнала)
![]() .
.
Очевидно
(рис. 3), что это условие выполняется при
![]() ,
при этом вероятность ошибки
,
при этом вероятность ошибки
 .
.
Отношение сигнал – шум по мощности
![]()
возрастает за счет большей разности математических ожиданий статистики.
1.5. Вероятность ошибок при передаче сигнала по каналу с гауссовым шумом
Одним из важнейших критериев производительности цифровых систем связи является зависимость вероятности появления ошибочного бита Pb от отношения энергии сигнала, приходящейся на один бит, к спектральной плотности мощности аддитивного белого гауссовского шума Eb/N0. При этом предполагается, что единственным источником искажений сигнала является тепловой шум ( АБГШ). Удобство использования отношения Eb/N0 вместо отношения мощности сигнала к мощности шума S/N, как в аналоговых системах связи, состоит в том, что так удобнее сравнивать производительность цифровых систем на битовом уровне. Это важно для цифровых систем, поскольку сигнал может иметь произвольное n-битовое значение (один символ может кодировать n бит). Предположим, что для данной вероятности возникновения ошибки в цифровом двоичном сигнале требуемое отношение S/N = 20. Поскольку двоичный сигнал имеет однобитовое значение, требуемое отношение S/N на бит равно 20. Пусть теперь сигнал является 1024-уровневым с теми же 20 единицами требуемого отношения S/N. Теперь, поскольку сигнал имеет 10-битовое значение, требуемое отношение S/N на один бит равно 2. Параметр Eb/N0 характеризует отношение сигнал-шум, приходящееся на один бит.
Параметр Eb/N0 связан с параметром S/N следующим соотношением:
![]()
где Tb — время передачи бита, N — мощность шума, R — скорость передачи битов, W — ширина полосы. Отношение R/W называется спектральной эффективностью системы или эффективностью использования полосы частот и выражается в бит/с/Гц. Это отношение показывает, насколько эффективно система использует полосу частот.
Далее в таблице 1 приводятся выражения для вероятности битовой ошибки (для бинарных модуляций и модуляции QPSK) и вероятности символьной ошибки (для M-арных модуляций).
Графики вероятности битовой ошибки для различных бинарных систем показаны на рис. 4.
Вид модуляции |
Вероятность ошибки на бит Pb или на символPS |
Примечание |
BASK |
|
Для ортогональных сигналов: S1(t)=Acoswt, S2(t)=0 0£t£T |
BPSK |
|
Для антиподных сигналов: S1(t)=Acoswt, S2(t)= - Acoswt, 0£t£T |
QPSK |
|
|
Ортогональная BPSK (когерентное обнаружение) |
|
|
Ортогональная BPSK (некогерентное обнаружение) |
|
|
DPSK (некогерентное обнаружение) |
|
|
DPSK (когерентное обнаружение) |
|
|
MPSK |
|
Для больших отношений ES/N0, ES=Eblog2M – энергия, приходящаяся на символ, M=2K – количество равновероятных символов |
DMPSK (некогерентное обнаружение) |
|
См. примечание для MPSK |
Ортогональная MFSK (когерентное обнаружение) |
|
ES=Eblog2M – энергия, приходящаяся на символ, M=2K – количество равновероятных символов |
Ортогональная MFSK (некогерентное обнаружение) |
|
См. примечание для MPSK с когерентным обнаружением |
QAM |
|
Для прямоугольной решетки; L – количество уровней амплитуды в одном измерении; используется код Грея |
Можно показать, что соотношение между вероятностью битовой ошибки и вероятностью символьной ошибки для ортогональных M-арных сигналов даётся выражением:
![]()
Аналогичное соотношение для многофазных сигналов MPSK при использовании кода Грея имеет вид:
![]()
Код Грея — это код преобразования бинарных символов в M-арные, такие, что двоичные последовательности, соответствующие соседним символам (сдвигам фаз), отличаются только одним битом. На рис. 5 обычная бинарная кодировка сравнивается с кодировкой Грея. При появлении ошибки в M-арном символе наиболее вероятными являются ближайшие соседние символы, отличающиеся от переданного лишь одним битом, если используется кодировка Грея. Таким образом, высока вероятность того, что при кодировании с помощью кода Грея в случае возникновения ошибки ошибочным будет только один из k = log2 M переданных битов.

Рис. 4. Вероятность битовой ошибки для различных бинарных систем

Рис. 5. Обычная кодировка (а) и кодировка Грея (б)
На рис. 6 приведены графики вероятности битовой ошибки для ортогональной M-арной (M = 2k) передачи сигналов с модуляцией MFSK с когерентным обнаружением, а на рис. 7 — графики вероятности битовой ошибки для многофазной (MPSK) передачи с когерентным обнаружением.
Как видно из сравнения этих рисунков, при ортогональной передаче с ростом k происходит уменьшение вероятности битовой ошибки, а при многофазной − увеличение.

Рис. 6. Зависимость вероятности битовой ошибки от Eb/N0 для ортогональной M-арной передачи сигналов по каналу с гауссовым шумом с помощью модуляции MFSK при использовании когерентного обнаружения

Рис. 7. Зависимость вероятности битовой ошибки от Eb/N0 для многофазной M-арной передачи сигналов по каналу с гауссовым шумом с помощью модуляции MPSK при использовании когерентного обнаружения

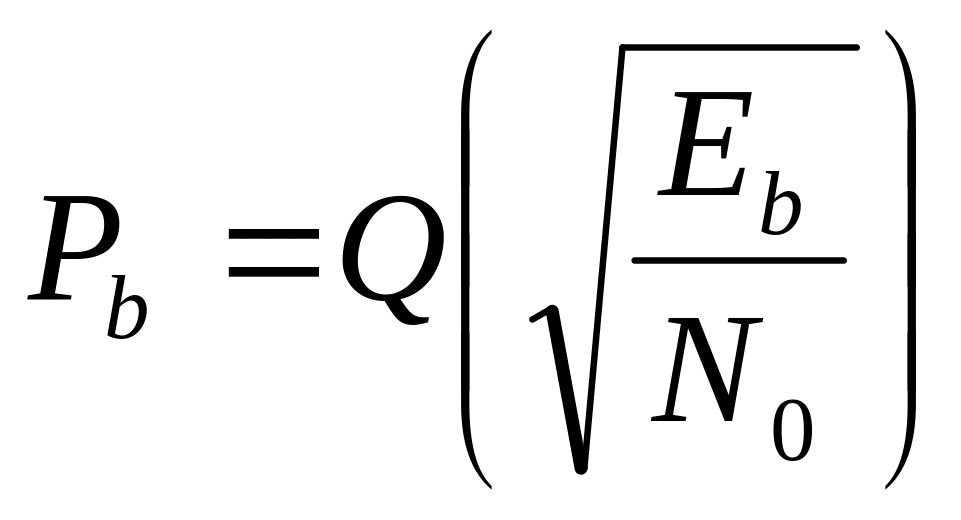 здесь
и далее
здесь
и далее