Примеры решения задач по квантовой механике

Задача. Найдите частоту красной границы фотоэффекта для металла, если при энергии падающих фотонов 6,6 эВ максимальная кинетическая энергия фотоэлектронов составляла 4,2 эВ. Постоянная Планка h = 6,610^34 Джс, е = 1,610^19 Кл. Ответ: 5,810¹⁴ Гц.

Решение.

Чтобы найти частоту красной границы фотоэффекта, нежно знать работу выхода электронов из металла. Работу выхода найдем из уравнения Эйнштейна:

Приравняв работу выхода к минимальной энергии фотонов, получим

Задача. Найдите максимальную скорость фотоэлектронов, вылетающих из металла с работой выхода 5 эВ под действием излучения с энергией квантов 10 эВ. Масса электрона m = 910^31 кг, заряд е = 1,610^19 Кл. Постоянная Планка h = 6,610^-34Джс. Ответ: 1,310⁶ м/с.

Решение.

Сначала найдем максимальную кинетическую энергию фотоэлектронов из уравнения Эйнштейна:

а потом по классической формуле кинетической энергии найдем максимальную скорость.

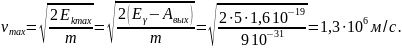
Задача. Микрочастица находится в квантовом состоянии, энергия которого с точностью до 0,01% равна 6,6 эВ. Оцените среднее время жизни частицы в этом состоянии. Постоянная Планка h = 6,610^34 Джс. Элементарный заряд е = 1,610^19 Кл. Ответ: 610^12 с.

Решение.

Согласно условию неопределенность значения энергии

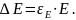
Используем соотношение неопределенностей

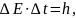
Задача. Рассмотрите все способы распределения двух частиц по двум состояниям для случаев: а) частицы квантовые с целочисленным спином; б) частицы квантовые с полуцелым спином. Ответ: 3 способа, 1 способ.

Решение.

Квантовые частицы с целочисленным спином являются бозонами, и в любом квантовом состоянии могут находиться в любом числе.

Сначала будем их размещать по одной частице в ячейке. Имеем один способ.

Теперь по две частицы в ячейке. Сначала в одной, потом в другой. Имеем еще два способа.

Квантовые частицы с полуцелым спином являются фермионами, и в любом квантовом состоянии могут находиться только в единственном числе.

Их можно разместить только по одной частице в ячейке. Имеем один способ.

Итак, две квантовые частицы с целочисленным спином по двум состояниям можно разместить тремя способами, а две квантовые частицы с полуцелым спином – одним способом.

Задачи по термодинамике

Задача. Посчитайте среднюю энергию молекулы данного газа.

Решение.

Средняя энергия молекулы газа зависит только от температуры газа и вычисляется по формуле

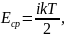
где 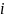– число степеней свободы молекулы данного газа. Это число зависит от количества атомов в молекуле газа.

Число атомов	1	2	3
	3	5	6

Задача. Посчитайте внутреннюю энергию некоторого количества данного газа.

Решение.

Внутренняя энергия заданного числа молей газа зависит только от температуры газа и вычисляется по формуле

Задача. Посчитайте изменение внутренней энергии некоторого количества данного газа.

Решение.

Изменение внутренней энергии заданного числа молей газа зависит только от температуры газа и вычисляется по формуле

Задача на вычисление работы газа , количества подведенного к нему тепла 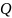и изменения его внутренней энергии .

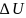Решение.

Эта задача предполагает применение уравнения первого начала термодинамики

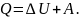
Все величины в этом уравнении могут быть как положительными, так и отрицательными.

Если газ получает тепло, , если газ отдает тепло, . В адиабатном процессе по определению .

Если газ нагревается, , если газ остывает, . В изотермическом процессе .

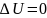Если газ расширяется, , если газ сжимается, . В изохорическом процессе .

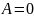При адиабатном расширении газ остывает, а при адиабатном сжатии газ нагревается.

Задача. Двум киломолям водяного пара сообщили количество теплоты, равное Q = 80000 Дж. Найдите изменение температуры, внутренней энергии и совершенную работу, если процесс изохорический. Газовая постоянная равна 8,31 Дж/мольК. Ответ: 1,6 К, 80000 Дж, 0.

Решение.

Так как по условию процесс изохорический, имеем . Тогда из уравнения первого начала термодинамики

Следовательно, изменение внутренней энергии газа равно 80000 Дж. Остается найти изменение температуры по формуле