3. Определение неизвестного движущего момента
Рисуют начальное звено (кривошип) механизма, т. е. у начального механизма отбрасывают стойку. К начальному звену по направлению угловой скорости ω1 прикладывают движущий момент М∂1 и на оси вращения кривошипа – силу тяжести G1. Действие на начальное звено отброшенных звеньев 2 и 3 заменяют соответствующими реакциями R21 и R31
Начальный механизм
1.
;
для первого звена
2.
;
для первого звена
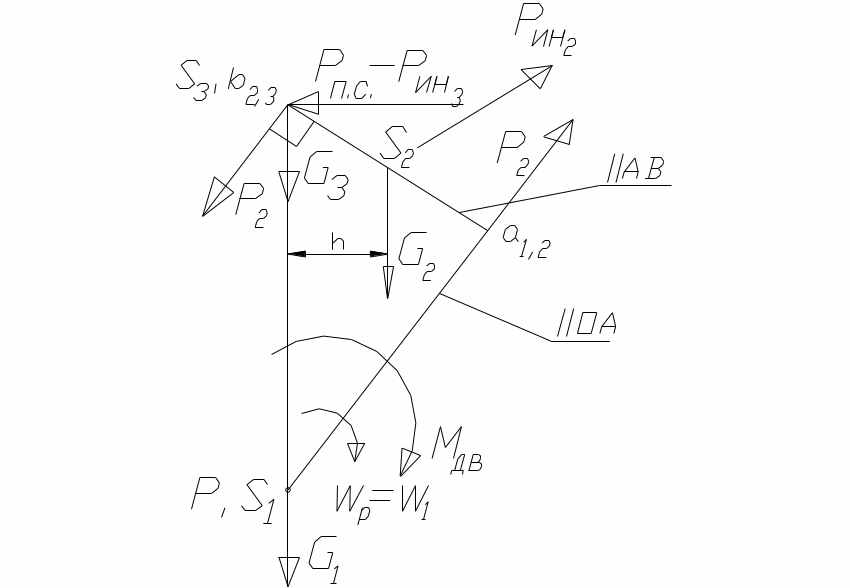
Построение рычага Жуковского и определение по нему Mдв.
Рычаг Жуковского и теоремы о нем.
Рычагом Жуковского называется жесткий рычаг переменной конфигурации в каждый момент времени, подобный плану скоростей, но повернутый на 90о против вращения начального звена (силовая модель механизма). Рычаг Жуковского фигура подвижная, он вращается с ωрычага = ω1
μv
;
если
Масштабный коэффициент Рычага Жуковского:
;
μр |
|
VA=Va
Теоремы о рычаге Жуковского.
Теорема 1. Скорость любой точки на механизме равна по величине и направлению скорости соответствующей точке на рычаге Жуковского.
μS μv μр
,
;
Следствие: Рычагом Жуковского можно пользоваться, как планом скоростей.
Теорема 2. Мощность силы, перенесенной с механизма параллельно самой себе в соответствующую точку рычага, равна мощности той же силы на механизме и определяется произведением угловой скорости рычага на момент этой силы относительно полюса рычага (если силу с механизма перенести параллельно самой себе на рычаг Жуковского, то мощность этой силы на механизме будет равна мощности той же силы на рычаге Жуковского).
Следствие: 
,
т.е. мощность любой силы равна моменту этой силы, относительно полюса рычага и угловой скорости рычага.
Теорема 3: Если все силы уравновешенные на механизме перенести параллельно, в соответствующие точки рычага, то сумма моментов всех сил относительно полюса рычага равны нулю.
Следствие: Для наложения движущего момента на начальное звено нужно: перенести с механизма на рычаг все силы параллельно себе в соответствующие точки, включая движущий момент; затем нужно составить сумму моментов относительно полюса рычага, и решить её относительно движущего момента.
Два способа переноса момента с механизма на рычаг Жуковского
При кинетостатическом исследовании механизмов используют два способа переноса моментов сил с механизма на рычаг Жуковского.
I способ: Момент силы приводят к двум точкам звена, направляя силы в этих точках согласно знаку момента
|
μр. |
|
II способ: Момент
силы переносят на рычаг Жуковского из
условия равенства их мощностей. Если
обозначить момент силы на механизме
через М, а на рычаге – через М΄, то
,где
–
мощность момента сил на механизме, на
рычаге. Тогда
|
μр
|
.
Направление
момента сил на рычаге определяют из
условия знаков
и
.
Если угловые скорости направлены в одну
сторону (у
один
и тот же знак), то момент силы не меняет
своего направления. При разных знаках
и
момент при переносе должен изменить
не только значение, но и направление.
Определение движущего момента по рычагу Жуковского и проверка результатов кинетостатического исследования
Итак, для нахождения движущего момента
строят рычаг Жуковского. На него переносят
все силы, включая силы инерции,
прикладывают неизвестный движущий
момент М∂2 на начальном звене и
решают уравнение моментов относительно
полюса рычага, т.е. уравнение вида:
Решая это уравнение моментов, находят
неизвестный движущий момент М∂2
на начальном звене исследуемого
механизма.
|
μv |
μр |
:
= 0
Достоверность результатов кинетостатического исследования проверяют по формуле:
