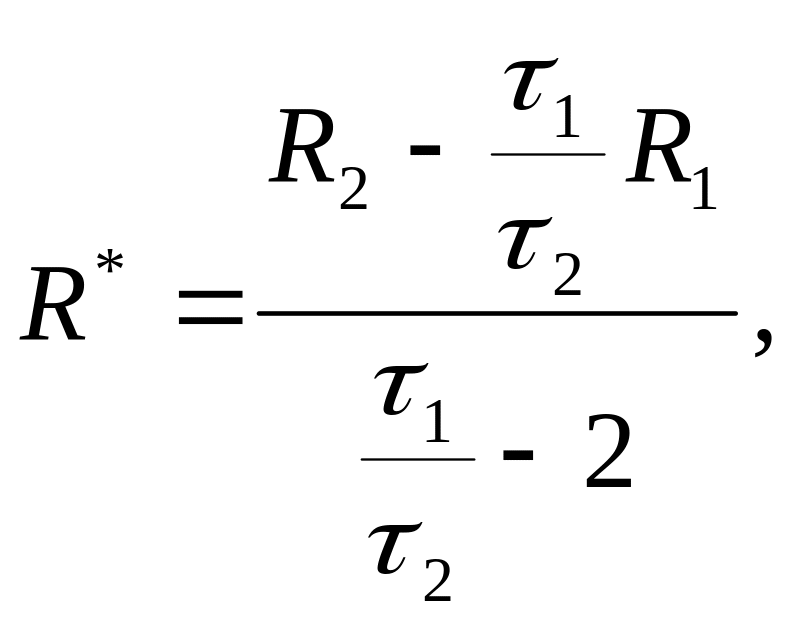- •Содержание
- •Введение
- •Лабораторная работа 1 Определение момента инерции тела
- •Литература:
- •Оборудование:
- •Основные теоретические сведения
- •Описание лабораторной установки
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Лабораторная работа №2 проверка законов математического маятника и Определение ускорения силы тяжести при помощи математического маятника
- •Литература
- •Цель работы
- •Оборудование
- •Основные теоретические сведения
- •Описание лабораторной установки
- •Порядок выполнения работы
- •Обработка полученных измерений
- •Контрольные вопросы
- •Лабораторная работа №3 Определение вязкости жидкости методом Стокса
- •Литература
- •Цель работы
- •Оборудование
- •Основные теоретические сведения
- •Описание лабораторной установки
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Лабораторная работа №4 Изучение зависимости коэффициента поверхностного натяжения от содержания поверхностно-активного вещества
- •Литература
- •Цель работы
- •Оборудование
- •Основные теоретические сведения
- •Порядок выполнения работы:
- •Лабораторная работа №5 Определение отношения теплоёмкости газов
- •Литература
- •Цель работы
- •Оборудование
- •Основные теоретические сведения
- •Описание лабораторной установки
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Лабораторная работа №6 Изучение и проверка закона Бойля-Мариотта
- •Литература
- •Оборудование
- •Основные теоретические сведения
- •Порядок выполнения работы
- •Контрольные вопросы
- •Лабораторная работа №7 Определение удельной теплоёмкости жидкости с помощью электрокалориметра
- •Литература
- •Цель работы
- •Оборудование
- •Основные теоретические сведения
- •Порядок выполнения работы
- •Контрольные вопросы
- •4. Зависит ли удельная теплоёмкость вещества от температуры?
- •Лабораторная работа №8 исследование электростатического поля
- •Литература
- •Цель работы
- •Оборудование
- •Основные теоретические сведения
- •Метод измерений
- •Измерительная установка
- •Порядок выполнения работы
- •Контрольные вопросы
- •Лабораторная работа №9 изучение работы источника эдс
- •Литература
- •Цель работы
- •Описание лабораторной установки
- •Порядок выполнения работы
- •Контрольные вопросы
- •Лабораторная работа №10 Методы электрических измерений
- •Литература
- •Цель работы:
- •Основные теоретические сведения
- •Порядок выполнения работы
- •Контрольные вопросы
- •Лабораторная работа №11 Определение горизонтальной составляющей вектора магнитной индукции Земли
- •Литература
- •Цель работы
- •Оборудование
- •Основные теоретические сведения
- •Порядок выполнения работы
- •Контрольные вопросы
- •Лабораторная работа №12 изучение петли гистерезиса и измерение параметров ферромагнетиков
- •Литература
- •Цель работы
- •Оборудование
- •Основные теоретические сведения
- •Порядок выполнения работы
- •Контрольные вопросы
- •Лабораторная работа №13 определение индуктивности соленоида
- •Литература
- •Цель работы
- •Оборудование
- •Основные теоретические сведения
- •Порядок выполнения работы
- •Порядок выполнения работы
- •Контрольные вопросы
- •Лабораторная работа №14 Исследование взаимной индукции работы трансформатора
- •14.1. Литература
- •Цель работы
- •Оборудование
- •Основные теоретические сведения
- •Порядок выполнения работы
- •Контрольные вопросы
- •Погрешности измерений физических величин
Порядок выполнения работы
Задание 1. Оценка индуктивности соленоида.
Подключите последовательно соединенные резистор R1 и катушку индуктивности L1 без ферромагнитного сердечника к генератору прямоугольных импульсов (рис. 13.3).
Подключите «Y» - вход осциллографа к резистору R1. На генераторе установите частоту 1200 Гц. Получите на экране устойчивую картину изменения напряжения на этом сопротивлении со временем, подобную изображенной на рис. 13.1.
Зная время развертки осциллографа, определите время релаксации τ, а затем, по формуле (8), вычислите величину индуктивности L1. При этом общее сопротивление цепи R можно приближенно заменить значением R1, пренебрегая внутренним сопротивлением генератора и активным сопротивлением катушки. Поэтому полученное численное значение индуктивности следует рассматривать как оценочное.
Повторите измерения L1, подключая другие резисторы. Проверьте, зависят ли получаемые значения индуктивности от сопротивления.
Приступите к измерению индуктивности вторым способом. Для этого подключите последовательно соединенные резистор R1 и катушку индуктивности L1 к звуковому генератору (рис. 13.4), установив на нем некоторое значение частоты в диапазоне 5÷ 15 кГц и некоторое значение амплитуды сигнала. (При таких частотах ток в цепи определяется в основном индуктивным сопротивлением катушки, что повышает точность измерения индуктивности).
С помощью осциллографа измерьте амплитудное значение падения напряжения на резисторе R1.
Отключите «Y»-вход осциллографа от резистора, а звуковой генератор от RL-контура и, не изменяя величину сигнала ЗГ, измерьте с помощью осциллографа амплитудное значение ЭДС генератора Е0 (рис. 12.5 лаб. Раб. №12).
Вычислите индуктивность по формуле (12).
Определите индуктивность, установив другие значения величин R, E0, ω. Проверьте, влияют ли эти параметры на результаты измерения.
Сравните результаты измерения индуктивности L1 двумя способами. Объясните различие этих результатов.
Задание 2. Измерение индуктивности соленоида.
Рассмотрим более подробно первый способ определения индуктивности, основанный на измерении времени релаксации.
Учтем, что общее активное сопротивление контура R равно сумме известного сопротивления R1 и неизвестного заранее сопротивления R*, обусловленного внутренним сопротивлением генератора, сопротивлением соединительных проводов, сопротивлением провода катушки соленоида:
![]()
Учитывая это, перепишем формулу (7) в виде
|
(13) |
Тогда время релаксации при подключении сопротивления R1 можно записать так:
|
(14) |
Это время можно измерить с помощью осциллографа с помощью схемы, изображенной на рис. 13.3.
Если заменить сопротивление R1 другим сопротивлением R2, то время релаксации станет равным
|
(15) |
Рассматривая (14) и (15) как систему двух уравнений с двумя неизвестными R* и L, находим
|
(16) |
|
(17) |
Формулы (17) позволяют, измерив τ1 и τ2, определить индуктивность соленоида с учетом R*, то есть существенно повысить точность измерения.
Теперь рассмотрим второй способ определения индуктивности L соленоида с помощью вынужденных электромагнитных колебаний в контуре.
Учтем, что в формулу (10) входит общее сопротивление контура, а в формулу (11) – напряжение на сопротивлении R1.
С учетом этого, приравниваем правые части формул (10) и (11):
|
(18) |
Выражая из (18) индуктивность получим:
|
(19) |
Формула
(19) переходит в (12) при
![]() ,
то есть при условии
,
то есть при условии
![]() .
Кроме того, из (19) видно, что точность
определения L
растет с ростом отношения
.
Кроме того, из (19) видно, что точность
определения L
растет с ростом отношения
 .
А это отношение велико, если в основном
падение напряжения происходит на
индуктивном сопротивлении:
.
А это отношение велико, если в основном
падение напряжения происходит на
индуктивном сопротивлении:
![]() .
Поэтому, как отмечалось выше, если
проводить измерения при достаточно
больших частотах ω, то можно получить
хорошую точность, используя упрощенную
формулу (12).
.
Поэтому, как отмечалось выше, если
проводить измерения при достаточно
больших частотах ω, то можно получить
хорошую точность, используя упрощенную
формулу (12).