Завдання

1. Вивчити теоретичні відомості.

2. Використовуючи приведений вище приклад програми MPI розробити блок-схеми загальної частини і окремих паралельних блоків обробки для реалізації процесу обчислення одинарного і подвійного інтеграла.

3. Написати MPI-програму обчислення інтеграла із таблиці 2.1.

4. Написати MPI-програму обчислення подвійного інтеграла із таблиці 2.2.

5. Відповісти на контрольні питання.

Зміст звіту

1. Тема і мета лабораторної роботи.

2. Завдання.

3. Блок-схеми та програмний код.

Варіанти завдань

Таблиця 2.1

№	Функції
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

Таблиця 2.2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

Контрольні питання

1. Як поводить себе паралельна программа в MPI при запуску?

2. Що повертає MPI при успішному завершенні виклику?

3. Назвіть стандартні комунікатори MPI?

Лабораторна робота № 3

Тема. Організація паралельного скалярного добутку векторів

Мета роботи: ознайомитися з прийомами створення паралельного програмного забезпечення; набути навичок реалізації розроблених блок-схем розпаралелювання послідовних алгоритмів скалярного добутку.

Короткі теоретичні відомості

Скалярний добуток двох векторів дорівнює сумі добутків їх відповідних координат.

Розглянемо алгоритм обчислення скалярного добутку двох n-мірних векторів. Нехай дано два вектори і . Їх скалярний добуток обчислюється за формулою: .

Оцінимо час, що витрачається на множення векторів. Нехай — час, що витрачається на множення двох чисел, — час складання двох чисел. Тоді час множення двох n-мірних векторів рівний: . Таким чином, складність алгоритму . Тепер розглянемо паралельний алгоритм обчислення скалярного добутку векторів. Позначимо через K кількість процесорів в системі, причому .

Тоді кожен процесор обчислюватиме координат результуючого вектора.

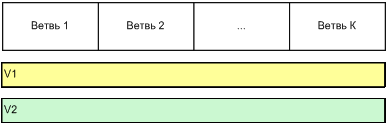
Рисунок 3.1 – Розподіл для скалярного добутку.

Розглянемо відношення .

З огляду на те, що ми бачимо, що використання паралельного алгоритму дозволяє вирішити задачу швидше. Більш того, при , паралельний алгоритм обчислює скалярний добуток векторів швидше послідовного майже в K разів.