Признаки мультиколлинеарности

Характерными признаками, при которых обычно возникает подозрение, что есть мультиколлинеарность, являются

1) Незначимые коэффициенты и при этом большой R² адекватная регрессия

2) Чувствительность оценок коэффициентов и оценок дисперсий коэффициентов к добавлению и исключению наблюдению из выборки.

40. Виды мультиколлинеарности. Строгая и нестрогая мультиколлинеарность

1. Строгая мультиколлинеарность – наличие линейной функциональной связи между объясняющими переменными (иногда также и зависимой).

2. Нестрогая мультиколлинеарность – наличие сильной линейной корреляционной связи между объясняющими переменными (иногда также и зависимой).

Строгая мультиколлинеарность нарушает одно из основных правил Гаусса-Маркова и делает построение регрессии полностью невозможным.Нестрогая мультиколлинеарность затрудняет работу, но не препятствует получению правильных выводов.

Последствия частичной мультиколлинеарности

Вид мультиколлинеарности, при котором факторные переменные связаны некоторой стохастической зависимостью, называется частичной. Если между факторными переменными имеется высокая степень корреляции, то матрица (XTX) близка к вырожденной, т. е.

det(XTX) ≈ 0.

Матрица (XTX)-1 будет плохо обусловленной, что приводит к неустойчивости МНК-оценок. Частичная мультиколлинеарность приводит к следующим последствиям:

· увеличение дисперсий оценок параметров расширяет интервальные оценки и ухудшает их точность;

· уменьшение t-статистик коэффициентов приводит к неверным выводам о значимости факторов;

· неустойчивость МНК-оценок и их дисперсий.

41. Понятие о мультиколлинеарности. Методы устранения мультиколлинеарности. Под мультиколлинеарностью понимается высокая взаимная коррелированность объясняющих переменных. 

Существует два основных подхода к решению этой задачи.

• Метод дополнительных регрессий

  • Строятся уравнения регрессии, которые связывают каждый из регрессоров со всеми остальными

  • Вычисляются коэффициенты детерминации   для каждого уравнения регрессии

  • Проверяется статистическая гипотеза   с помощью F-теста

Вывод: если гипотеза   не отвергается, то данный регрессор не приводит к мультиколлинеарности.

• Метод последовательного присоединения

  • Строится регрессионная модель с учетом всех предполагаемых регрессоров. По признакам делается вывод о возможном присутствии мультиколлинеарности

  • Расчитывается матрица корреляций и выбирается регрессор, имеющий наибольшую корреляцию с выходной переменной

  • К выбранному регрессору последовательно добавляются каждый из оставшихся регрессоров и вычисляются скорректированные коэффициенты детерминации для каждой из моделей. К модели присоединяется тот регрессор, который обеспечивает наибольшее значение скорректированного 

Процесс присоединения регрессоров прекращается, когда значение скорректированного   становится меньше достигнутого на предыдущем шаге.

Каким бы образом не осуществлялся отбор факторов, уменьшение их числа приводит к улучшению обусловленности матрицы  , а, следовательно, и к повышению качества оценок параметров модели.

Помимо перечисленных методов существует ещё один, более простой, дающий достаточно хорошие результаты — это метод предварительного центрирования. Суть метода сводится к тому, что перед нахождением параметров математической модели проводится центрирование исходных данных: из каждого значения в ряде данных вычитается среднее по ряду:  . Эта процедура позволяет так развести гиперплоскости условий МНК, чтобы углы между ними были перпендикулярны. В результате этого оценки модели становятся устойчивыми

42. Спецификация и оценивание МНК эконометрических моделей нелинейных по параметрам. В моделях, нелинейных по параметрам (степенных или показательных) применение ^ МНК для оценки невозможно, т.к. необходима линейность по коэф-там уравнения регрессии. Поэтому преобразуют(линеаризуют) через логарифмирование.  1. Рассмотрим уравнение парной регрессии вида Y = A*X^β, где А и β— параметры модели. Параметр А - значение эндогенной переменной при единичном значении регрессора. Продифференцируем ур-е по Х: 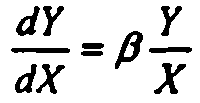=> 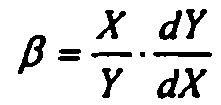т. е. параметр β - эластичность Y по X. Прологарифмируем обе части ур-я:  где α=ln(A). Это двойная логарифмическая модель:  (модель с постоянной эластичностью). Ур-е линейно относительно логарифмов переменных, => введя: ,получаем специф-ю линейной модели, к кот. применим МНК: (произв. ф-я, спроса, потребл-я..) 2. Спецификации линейных моделей, включающих или только логарифмы значений эндогенной переменной, или только логарифмы значений регрессора – это полулогарифмические.  - лог-линейная модель. Используем замену Y* = ln(У). Продифференцируем по X:  т. е. параметр имеет смысл темпа прироста Y по X.(наращивание суммы при неприрывной процентной ставке) 3.Линейно-логарифмическая модель:  Замена X* = ln(X). Продифференцировав по X, получим:  , откуда 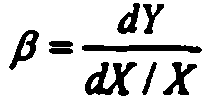 т. е. параметр характеризует отношение абсолютного изменения Y к относительному изменению Х (моделирование влияния процентного изменения денежной массы на изменение объема ВНП).

43. Способы включения случайных возмущений в спецификацию нелинейной по параметрам модели. Случайные возмущения в линейных регрессионных моделях должны удовлетворять условиям Гаусса—Маркова, только тогда МНК-оценки будут состоятельными, несмещенными и эффективными. Поэтому при линеаризации нелинейных регрессионных моделей важен этап включения случайного возмущения в исходное уравнение. В моделях логарифмического типа для линеаризации используется операция логарифмирования. Этому же преобразованию подвергается и случайное возмущение. Чтобы в линейное ур-е после линеаризации возмущение входило аддитивно, в исходную нелинейную спец-ю оно должно включаться мультипликативно,

Например, возможны следующие способы включения случайного возмущения –

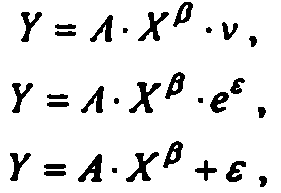
где v, ɛ— случ-е возмущения. Модель при линеаризации преобразуется в парную логарифмическую модель: , где α=ln(A). Случайное возмущение ɛ=ln(ν) включено в линейную спец-ю аддитивно. Чтобы оно удовлетворяло условиям нормальной линейной регрессионной модели , возмущение v

исходной нелинейной спецификации должно иметь логарифмическое нормальное распределение с параметрами: . Значение ɛ=ln(ν)=0, при v=1, что не приводит к изм-м значений эндогенной переменной. Аналогично для второго вида ур-я регрессии, но случайное возмущение ɛ имеет нормальное распределение с параметрами , а не логарифмически нормальное. Поэтому применение МНК не вызывает затруднений. Значение ɛ = 0 не приводит к изм-м значений эндогенной переменной в спецификации. Для 3 модели логарифмирование не приводит к линейной модели: , поэтому непосредственное применение обычного МНК невозможно. Для оценки параметров таких нелинейных моделей разработан нелинейный метод наименьших квадратов.

44. Спецификация и оценивание МНК эконометрических моделей нелинейных по переменным. В моделях, нелинейных по переменным, регрессоры, имеющие степень отличную от первой, заменяются другими независимыми переменными первой степени, и к новой системе переменных применяется обычный МНК. После того как получено уравнение с оцененными параметрами, введенные в него новые независимые переменные заменяются на первоначальные.

Например, пусть необходимо оценить параметры модели

Введем переменные:

Оценка вектора параметров: . Если предпосылки Гаусса—Маркова выполнены для исходной спецификации, то они выполняются и для преобразованной. Аналогично для полиномиальной регрессии степени р:

β0 —начальный уровень; β1-скорость роста и т.д.

Для преобразования гиперболической регрессии к линейному виду используется замена: .

а - уровень эндогенной переменной, который устан-ся при больших значениях регрессора, а параметр b- скорость приближения к данному уровню (пр: зависимость спроса от цен или дохода, кривая Филлипса). Для регрессии вида , замена: . Для спецификации , замена как для эндогенной переменной, ,так и регрессора .