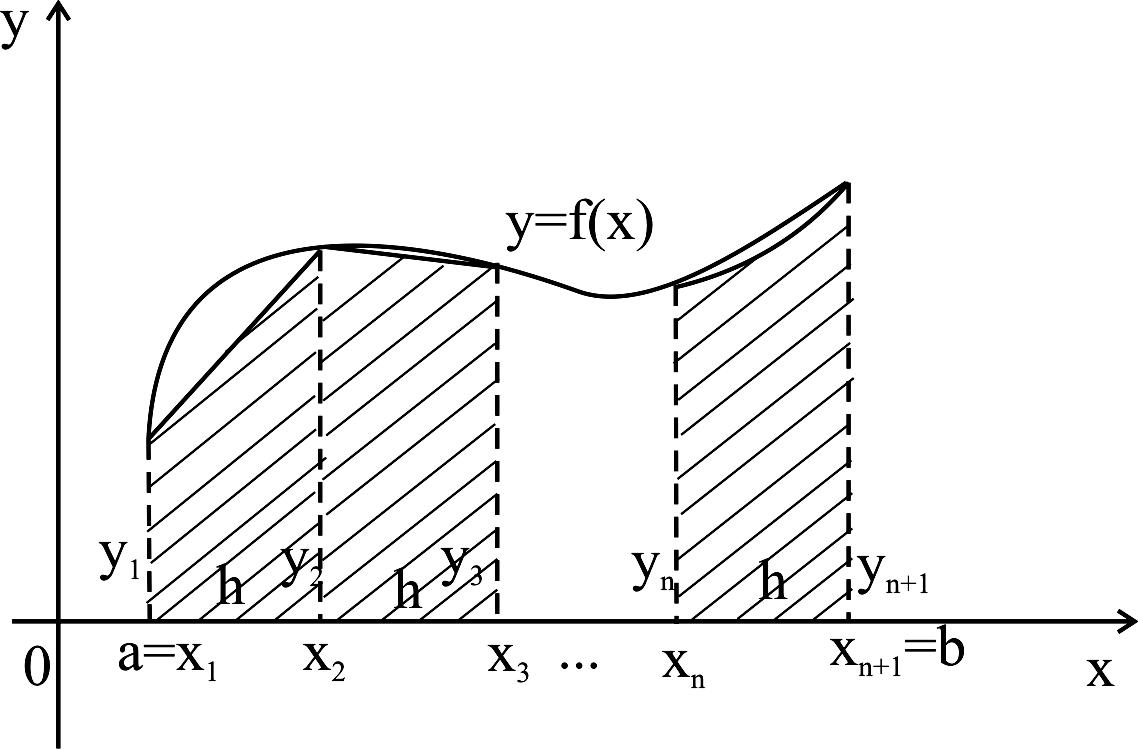
9.3 Метод трапеций

Подынтегральную функцию заменим функцией, представляющей собой ломаную линию, звенья которой соединяют концы ординат и (рисунок 35). В этом случае площадь криволинейной трапеции заменим на сумму площадей трапеций с основаниями , и высотой :

или

(9.7)

Ф

ормула (9.7) называется формулой трапеций. Ее погрешность может быть оценена следующим образом:

(9.8)

где .

Рисунок 35

9.4 Метод Симпсона

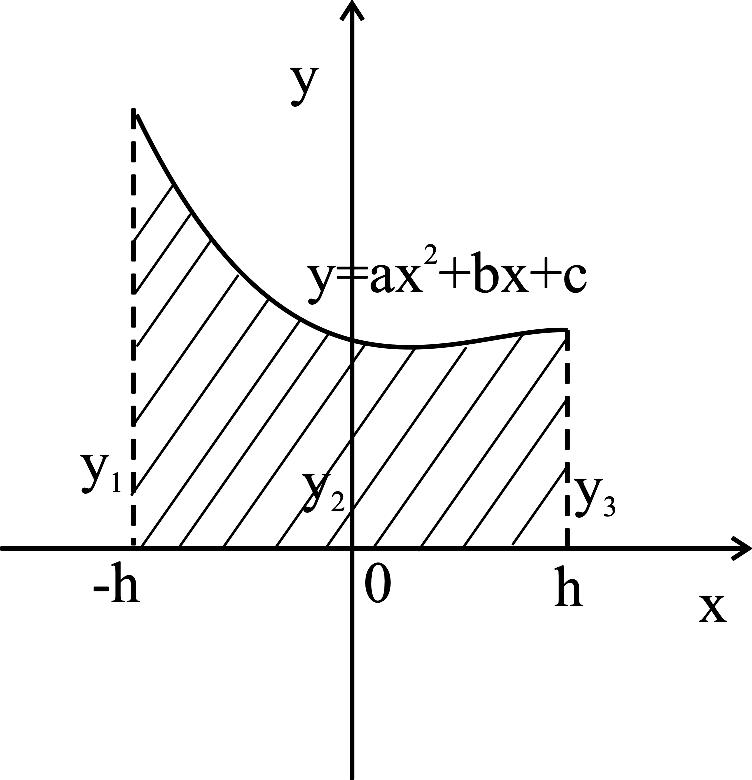
Этот метод приближенного вычисления определенного интеграла основан на замене графика подынтегральной функции не ломаной, как в методе трапеций, а дугами парабол, оси симметрии которых параллельны оси .

Рассмотрим сначала как находится площадь криволинейной трапеции, ограниченной на отрезке дугой параболы (рисунок 36):

(9.9)

П

опробуем связать вычисления площади

со значениями функции в

точках ;

; .

Умножим второе уравнение на 4 и сложим

все уравнения:

Тогда площадь , определяемая (9.9), Рисунок 36

может быть вычислена следующим образом:

. (9.10)

(9.10) называется малой формулой Симпсона (Т.Симпсон (1710-1761) – английский математик).

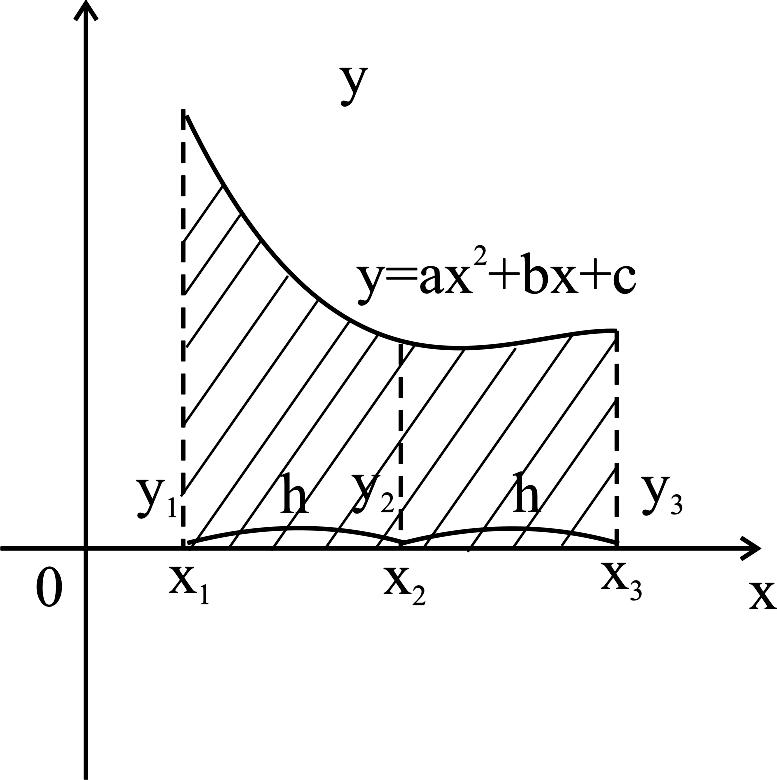
Сдвинем параболу вдоль оси (рисунок 37) так, что . В этом случае малая формула Симпсона (9.10) остается также справедливой, так как при параллельном переносе кривой величины

у

и площадь криволинейной трапеции не изменяются. Следовательно, в формуле (9.10)

- ордината параболы на левом

конце отрезка (при );

- ордината параболы на правом конце отрезка (при );

- ордината параболы в средней точке отрезка , т.е. в точке

Рисунок 37 .

Рассмотрим теперь криволинейную трапецию, ограниченную произвольной кривой на отрезке (рисунок 38).

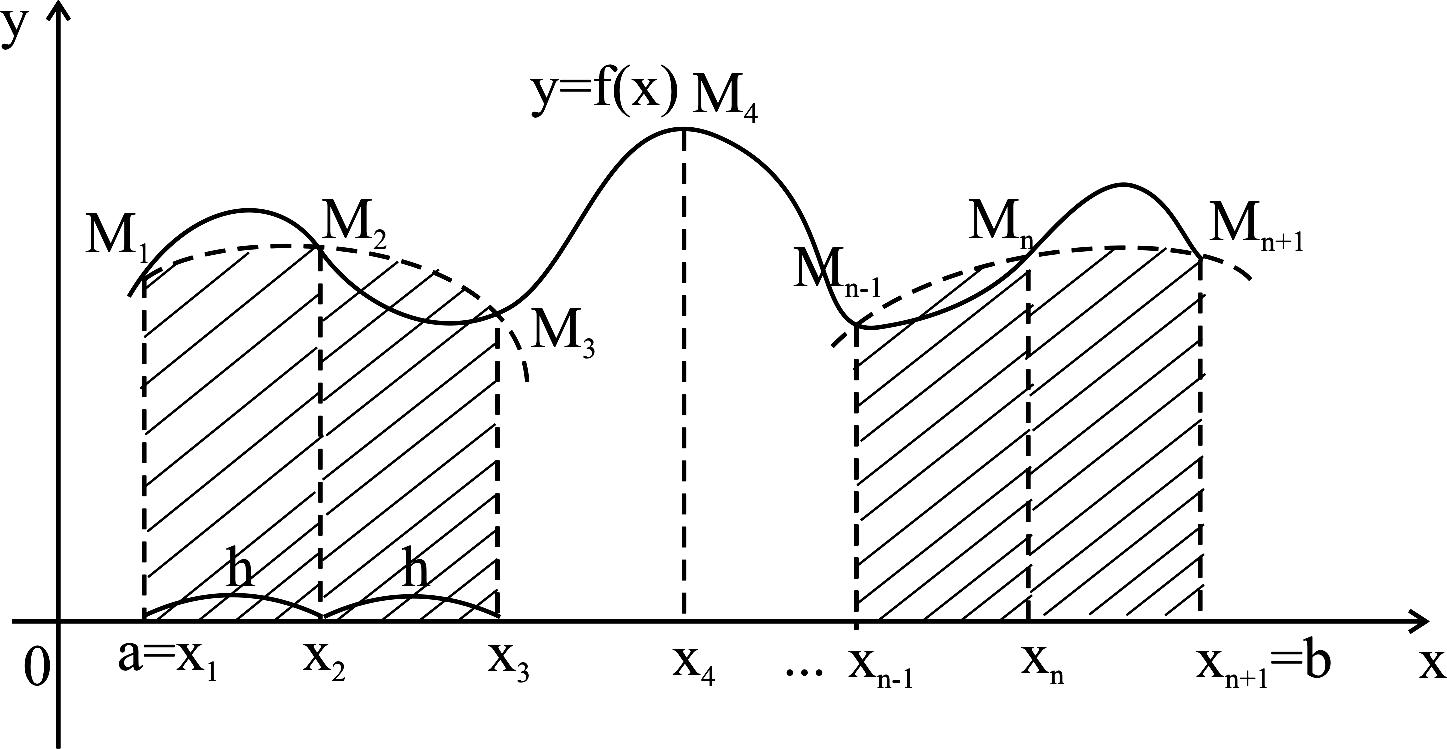
Рисунок 38

Разобьем отрезок на четное число равных частей, т.е. . Длина каждого отрезка равна по (9.1) . Объединим частичные отрезки попарно и заменим каждую криволинейную трапецию с основанием такой, которая сверху ограничена не кривой , а параболой, проведенной через соответствующие три точки этой кривой:

. Можно показать, что эти параболы определяются однозначно. Площадь каждой такой трапеции с основанием вычислим по малой формуле Симпсона (9.10), а площадь всей криволинейной трапеции приближенно равна их сумме:

Тогда

(9.11)

и формула (9.11) называется формулой Симпсона, а ее погрешность оценивается так:

где (9.12)

Замечания 1. Приближенные формулы вычисления определенного интеграла выведенные в предположении, что , остаются справедливыми для любой функции , непрерывной на отрезке .

2. Оценки погрешностей вычисления определенного интеграла с использованием приближенных формул достаточно сложны, поэтому на практике обычно поступают следующим образом:

а) задают точность вычисления ;

б) вычисляют значения интеграла по одной из приближенных формул (трапеций или Симпсона, как наиболее точных) и при числе точек деления и ;

в) сравнивают результаты вычислений, находя их разность по модулю . Если она меньше заданной точности , то вычисления прекращают и записывают, что (или ). Если же разность больше, чем , то вновь удваивают число точек деления и находят . Сравнивая с делают вывод о прекращении или продолжении процесса удваивания точек деления.

Пример 9.1 Дан интеграл . Найти:

1. точное значение по формуле Ньютона-Лейбница;

2. приближенное значение по формулам прямоугольников, трапеций, Симпсона, разбив отрезок интегрирования на 10 равных частей. Все промежуточные вычисления производить с округлением до четвертого десятичного знака;

3. сравнить полученные результаты с точным значением интеграла, найдя абсолютную и относительные погрешности для каждой из формул, сделать выводы.

Решение. 1) Вычислим данный интеграл, т.е. найдем его точное значение, применяя замену переменной:

.

2) Для вычисления интеграла по приближенным формулам составим таблицу 1 значений подынтегральной функции при разбиении отрезка интегрирования на 10 равных частей и шаге . Так как в формулы входят значения функции с четными и нечетными индексами, то для быстроты вычислений выделим эти значения отдельно друг от друга в столбцах таблицы 1.

Вычислим приближенное значение интеграла по формуле прямоугольников (9.3):

которую для удобства вычислений перепишем в виде:

(9.13)

где

Таблица 1 – Значения подынтегральной функции

i	xi	y1, y11	yi, (i – четное)	yi, (i – нечетное)
1 2 3 4 5 6 7 8 9 10 11	15 23,4 31,8 40,2 48,6 57,0 65,4 73,8 82,2 90,6 99
	-

Так как подынтегральная функция возрастает на отрезке интегрирования [15; 99] (см. ее значения в таблице1), то используя формулу (9.13), мы получаем приближенное значение исходного интеграла с недостатком:

.

Абсолютная погрешность вычислений определяется как разность между точным и приближенным значениями интеграла, взятая по абсолютной величине:

. (9.14)

Тогда . Относительная погрешность вычислений определяется как отношение абсолютной погрешности к точному значению интеграла, взятое в процентах:

. (9.15)

Относительная погрешность для формулы прямоугольников с недостатком составит: .

Вычислим приближенное значение интеграла по формуле прямоугольников (9.4): которую запишем в виде:

(9.16)

Тогда, - приближенное значение интеграла с избытком.

Находим, какова относительная и абсолютная погрешности при использовании формулы прямоугольников с избытком:

Для получения более точного значения данного интеграла можно взять среднее арифметическое значений, полученных по формулам прямоугольников:

Найдем приближенное значение интеграла, используя формулу трапеций (9.7), которую так же перепишем через суммы четных и нечетных значений функции:

(9.17)

Имеем:

Погрешности вычислений составят:

.

Вычислим интеграл по формуле Симпсона (9.11), переписав ее следующим образом:

(9.18)

Тогда для данного интеграла:

.

Абсолютная и относительная погрешности формулы Симпсона составят:

.

Сравнивая полученные результаты, можно сделать вывод, что в данном случае формула Симпсона дает наилучшее приближение к точному значению интеграла.