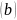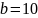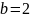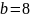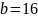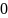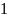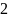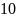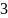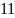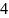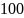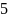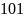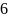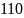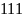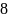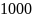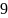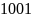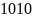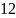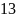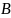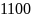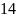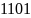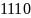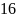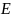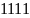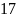Теоретические основы информатики.

Система счисления — символический метод записи чисел, представление чисел с помощью письменных знаков.

Непозиционная система счисления — система счисления, в которой значение цифры не изменяется в зависимости от её расположения.

Пример: римская система.

Позиционная система счисления — система счисления, в которой значение каждого числового знака (цифры) зависит от его позиции (разряда).

Позиционная система счисления определяется целым числом b>1, называемым основанием системы счисления. Система счисления с основанием b так же называется b-ричной. (в частности, двоичной, троичной, десятичной)

Целое число x в b-ричной системе счисления представляется в виде конечной линейной комбинации степеней числа b.

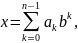
где — это целые числа, называемые цифрами, удовлетворяющие неравенству .

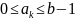Каждая степень 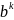в такой записи называется разрядом, старшинство разрядов и соответствующих им цифр определяются значением показателя степени .

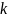Например, число 2057 в десятичной системе счисления представляется в виде: .

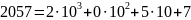В цифровых устройствах используется двоичная система счисления.

Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления числа записываются с помощью двух символов (0 и 1).

Двоичная система соответствует требованиям:

Чем меньше значений существует в системе, тем проще создать устройства, оперирующие этими значениями.
Чем меньше количество состояний элемента, тем выше помехоустойчивость, и тем быстрее он может работать.
Двоичная арифметика довольно проста. Простыми являются таблицы умножения и сложения — основных действий над числами.

Восьмери́чная систе́ма счисле́ния — позиционная целочисленная система счисления с основанием 8. Для представления чисел в ней используются цифры от 0 до 7.

Восьмеричная система часто используется в областях, связанных с цифровыми устройствами. Характеризуется лёгким переводом восьмеричных чисел в двоичные и обратно, путём замены восьмеричных чисел на триплеты двоичных. Ранее широко использовалась в программировании и вообще компьютерной документации, однако в настоящее время почти полностью вытеснена шестнадцатеричной.

Широко используется в низкоуровневом программировании и компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами.

В стандарте Юникода номер символа принято записывать в шестнадцатеричном виде, используя не менее 4 цифр.

Шестнадцатеричный цвет — запись трёх компонент цвета (R, G и B) в шестнадцатеричном виде.

Значения чисел в некоторых системах счисления.