Основы радиосхемотехники / Учебник по САЭУ(2005) / САЭУ кн.1 / Гл 4

99

На рисунке  -комплексные Y-пара­метры выходной цепи биполярного транзи­сто­ра, g_К – проводи­мост­ь сопротивле­ния коллектора. Ввиду большой емкости кон­денсатора C_Э сопротив­ление участка эмиттер- общий провод схемы рис.4.6 во всем диапазоне рабочих частот полагается равным нулю. Следовательно, последовательная отрицательная обрат­ная связь по переменному току в каскаде отсутствует, а эмиттер транзистора в схеме рис.4.8 оказывается подключенным к общему проводу. Аналогично исследованию каскада с полевым транзистором весь частотный диапазон разделяется на три участка. В области низких частот полагаем: а , т.е. проводимости и сопротивления считаются действительными, при этом конденсатор С_Р учитывается; тогда схема рис.4.8 и комплексный коэффициент совпадают с аналогичным для каскада на полевом транзисторе: , где (4.9)

- коэффициент усиления напряжения в области средних частот - постоянная выходной цепи в области нижних частот. В области средних частот полагается частотная независимость комплексных параметров

,

сопротивление конденсатора С_Р оказывается существенно меньше сопротивления нагрузки R_Н, тогда разделительный конденсатор из схемы исключается и эквивалентные схемы рис.4.8 (при отсутствии конденсатора С_Р) ирис.4.3,б совпадают, при этом

.

В области верхних частот учитывается комплексный характер и Z_H, а сопротивление конденсатора С_Р полагается малым по сравнению с сопротивлением нагрузки. В этом случае топология эквивалентной схемы выходной цепи совпадает с топологией схемы рис.4.3,в. Тогда:

Подставляя в последнее соотношение Y₂₁ и Y₂₂ из выражений для комплексных Y- параметров биполярного транзистора с общим эмиттером, получим:

(4.10)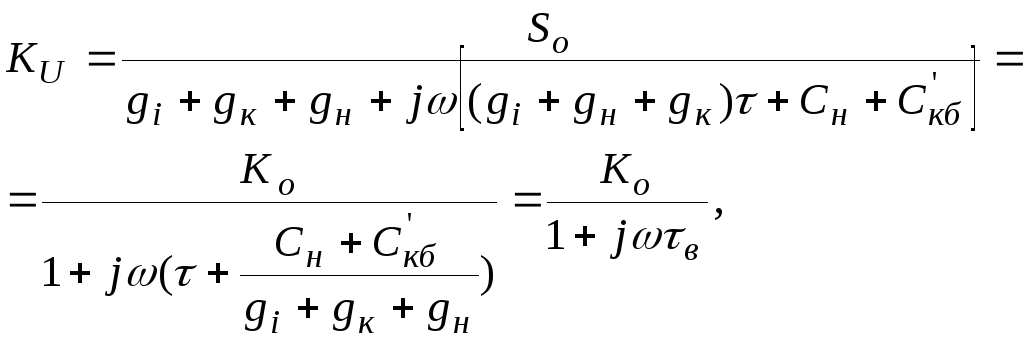

г

де - постоянная выходной цепи каскада для области верхних частот. Выражение (4.10) совпадает с (4.4). Следовательно, характер частотных и фазовых искажений в области высоких частот у резисторного каскада с биполярным и полевым транзистором одинаковый.

Исследуем входную цепь каскада, эквивалентная схема которой приведена на рис4.9.

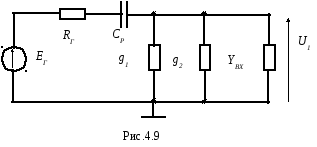
В области нижних частот топология схем рис.4.9 и 4.3а оказывается одинаковой. Следовательно:

,

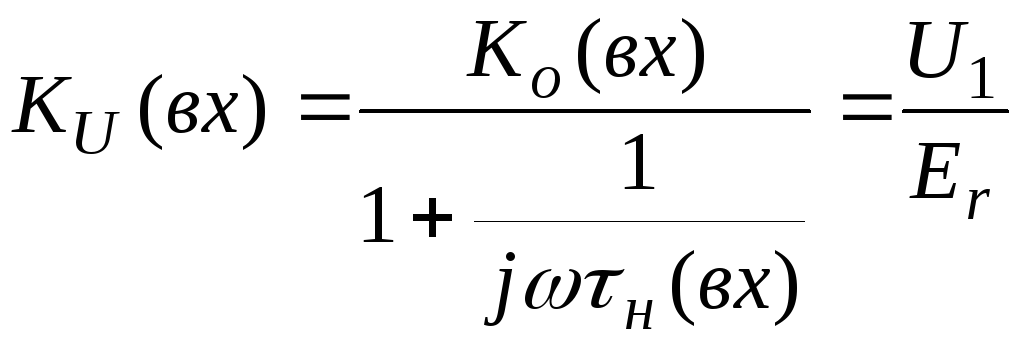где

-

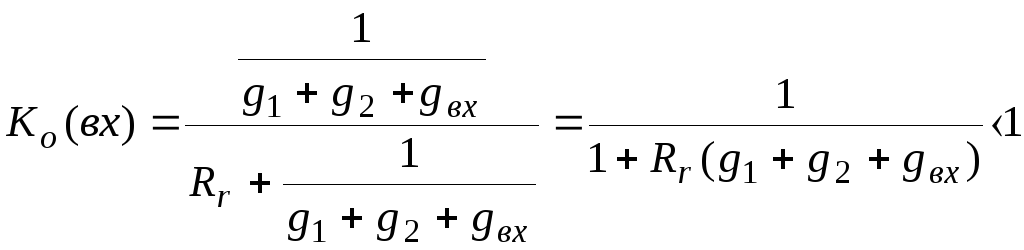коэффициент ослабления сигнала во входной цепи в области средних частот,

- постоянная цепи для нижних частот. В области средних частот пренебрегаем сопротивлением конденсатора С_Р:

тогда схема рис.4.9 преобразуется к виду изображенному на рис.4.10.

Следовательно:

.

В области верхних частот в схеме рис.4.9 учитывают комплексный характер входной проводимости Y_ВХ и пренебрегают сопротивлением разделительного конденсатора; при этом в рабочем диапазоне частот обычно выполняется соотношение: тогда входная проводимость:

,

где g_ВХ~g₁₁, C_ВХ(g)=τ/r_Б+С_КБ К₀

-максимальная входная динамическая емкость каскада с биполярным транзистором. В этом случае схема рис.4.9 преобразуется в схему, приведенную на рис.4.11.

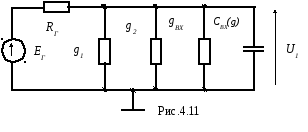
Из рисунка следует, что , где - постоянная входной цепи.

Таким образом, комплексные коэффициенты передачи входной и выходной цепи резисторных каскадов на полевых и биполярных транзисторах имеют одинаковую структуру. Следовательно, характер частотных и фазовых искажений сигнала в этих цепях одинаковый. В количественном отношении искажения зависят от постоянных , , в выходной и входной цепи каскада на полевом или биполярном транзисторе.

4.1.1.1.Переходные характеристики

Исследуем переходные процессы в выходных и входных цепях резисторных каскадов при возбуждении их сигналами в виде единичных скачков: .

Рассмотрим эквивалентную схему выходной цепи полевым транзистором, рис.4.12. На рисунке штриховыми линиями выделены коллекторные проводимости выходной цепи усилительного элемента – параметрY₂₂, и нагрузки.

Зависимость тока генератора от времени представляет собой функцию единичного скачка с амплитудой:

при , при

Емкость конденсаторов С_ис, С_зс, С_н составляет единицы и десятки пФ, емкость разделительного конденсатора С_р - - мкФ или более. Появление скачка тока S_oU₁ вызывает в схеме переходный процесс, при котором все конденсаторы заряжаются. Поскольку напряжение на конденсаторе:

,

то скорость его заряда

обратно пропорциональна величине его емкости С. Поэтому в течение достаточно малого интервала времени интенсивно заряжаются конденсаторы С_ИС, С_ЗС, С_Н .Конденсатор С_Р существенно большей емкости за этот интервал оказывается практически не заряжен, а его сопротивление и напряжение на нём будут близки к нулю. После заряда конденсаторов малой ёмкости ток в них прекращается, их сопротивление оказывается очень большим, поэтому при дальнейшем исследовании переходного процесса эти конденсаторы можно исключить из эквивалентной схемы.

Временной интервал переходной функции U₂(t), где интенсивно заряжаются межэлектродные емкости усилительного элемента и нагрузки называют областью малых временных интервалов (областью малых времен). Эквивалентная схема рис.4.12 для области малых времен совпадает при этом со схемой выходной цепи, справедливой для области верхних частот, рис.4.3,в.

После окончания заряда конденсаторов малой емкости можно выделить интервал времени, при котором напряжение на разделительном конденсаторе еще достаточно мало. Для этого временного интервала, где напряжением на конденсаторе С_Р пренебрегают, называемого областью средних времен, справедлива эквивалентная схема, изображенная на рис.4.12а, она совпадает со схемой выходной цепи каскада, справедливой для средних частот -рис.4.3.б.

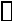
S₀U₁(t)

g_i

g_C

g_H

U₂(t)

Рис.4.12 а

Ин­тервал времени пере­ходной харак­тери­стики U₂(t), в котором на­пряжение на конденса­торе C_P становится сравнимым с напряже­нием на нагрузке R_н и даже превышает его, на­зывают областью боль­ших времен. Эк­вивалентная схема для этого временного интер­вала, очевидно, совпадает со схемой рис.4.3а, справедливой для области нижних частот.

Определим переходную характеристику для указанных интервалов времени, используя операторный метод прямого и обратного преобразования Лапласа.

Область малых временных интервалов

Используя выражение комплексного коэффициента передачи напряжения в области верхних частот, запишем оператор цепи:

,

где - изображения по Лапласу выходного и входного сигналов. Для функции изображение по Лапласу будет: . Следовательно, изображение выходного сигнала:

Переходя от изображения по Лапласу к оригиналу, запишем:

(4.11)

Очевидно, полюсы: p₁, p₂ подынтегральной функции (4.11) располагаются в начале координат: р₁=0 и на отрицательной действительной оси: . Поэтому, переходя от линейного интеграла (4.11) к контурному с бесконечно большим радиусом, охватывая им сначала всю левую полуплоскость, а затем к двум контурным интегралам С₁, С₂, охватывающим полюсы р₁и p₂,запишем:

Для вычисления интегралов в последнем выражении воспользуемся формулой Коши:

где контур С охватывает полюс р_о, а f(p) – аналитическая функция комплексного переменного р. Поэтому контурный интеграл C₁ для первого полюса Р₁ согласно формуле Коши дает:

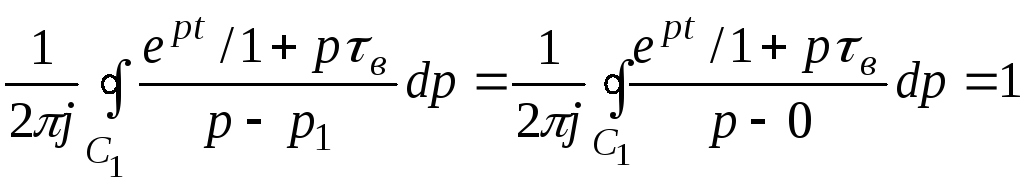
Для вычисления второго контурного интеграла преобразуем его к виду совпадающему с формулой Коши:

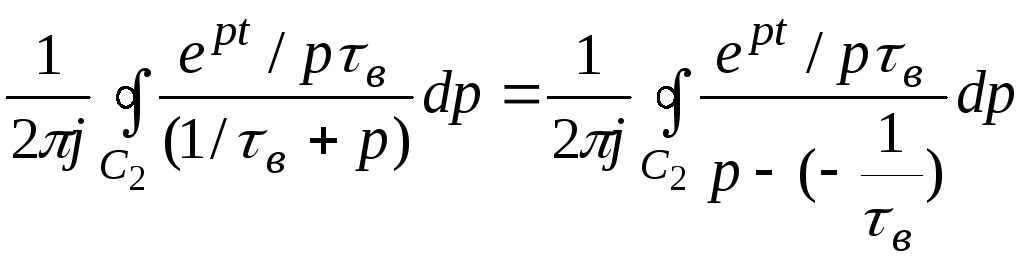
Тогда:

.

Следовательно, переходный процесс для области малых времен будет записан в виде:

.