Список использованных источников

1. Андрющенко, А.И. Основы термодинамики циклов теплоэнергетических установок / А.И. Андрющенко. – М.: «Высшая школа», 1985. – 319 с.

2. Варгафтик, Н.Б. Справочник по теплофизическим свойствам газов и жидкостей / Н.Б. Варгафтик. – М.: «Наука», 1972. – 720 с.

3. Ривкин, С.Л. Термодинамические свойства воды и водяного пара. Справочник / С.Л. Ривкин, А.А. Александров. – М.: «Энергоатомиздат», 1984. – 80 с.

4. Маргулова, Т.Х. Атомные электрические станции / Т.Х. Маргулова. – М.: «Высшая школа», 1978. – 360 с.

5. Кириллин, В.А. Техническая термодинамика / В.А. Кириллин, В.В. Сычев, А.Е. Шейндлин. – М.: «Энергия», 1974. – 448 с.

Тема 10 Показатели термодинамической эффективности на разных стадиях анализа тэу

Реферативное изложение темы

Три этапа анализа циклов и, соответственно, три КПД цикла: термический КПД ( ), внутренний абсолютный КПД ( ) и эффективный КПД цикла установки в целом ( ). Математическая и терминологическая тонкость при анализе циклов через посредство формул для КПД.

Рассматривая общие принципы построения термодинамических циклов теплоэнергетических установок (ТЭУ), анализируя эти циклы, мы пользовались понятием термического КПД цикла , определяемого по формуле

, (10.1)

здесь «обр» – означает обратимый процесс.

Если теперь подведенное в цикле тепло и отведенное тепло раскрыть через энтальпии в соответствующих точках обратимого цикла, обозначенных на рисунке 10.1, то получим следующее выражение для

(10.2)

здесь – изоэнтропный (адиабатический) теплоперепад в турбине (адиабатическая работа расширения); – изоэнтропный (адиабатический) теплоперепад в насосе (или компрессоре), другими словами – адиабатическая работа сжатия.

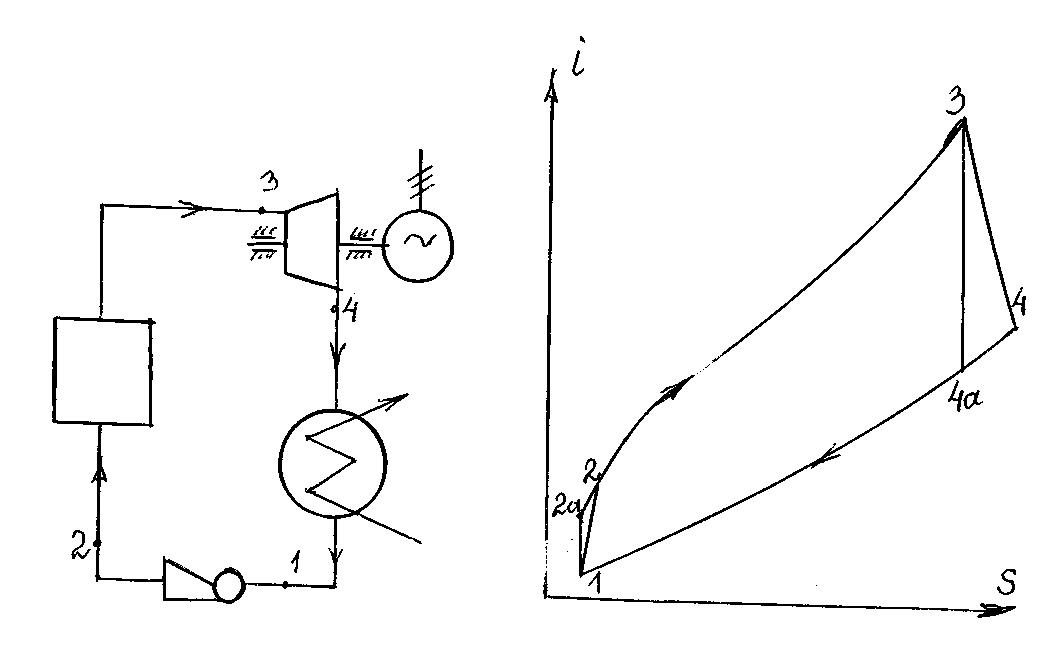
Рисунок 10.1 – Принципиальная тепловая схема ТЭУ и

i-s диаграмма цикла данной установки

Для оценки термодинамической эффективности ТЭУ следует ответить на две группы основных вопросов:

1. Насколько велик КПД обратимого цикла, от каких факторов он зависит и что следует предпринять для его увеличения? На этом этапе показателем эффективности служит термический КПД обратимого цикла .

2. Насколько велики необратимые потери в реальном цикле установки, как распределяются эти потери по отдельным элементам цикла и, следовательно, на усовершенствование какой части цикла ТЭУ надо обратить внимание с целью уменьшения степени необратимости цикла? Эти вопросы решаются на последующих этапах.

Потери от необратимости в процессе расширения рабочего тела в турбине выливаются в повышение энтропии; реальный процесс идет не по изоэнтропе 3-4а, а по политропе 3-4. А работа расширения в реальном процессе снижается и становится равной Δi_Т = i₃ – i₄. Разность i₄ –i_4а необратимо превращается в тепло трения. Отношение действительной работы расширения к теоретической называется внутренним относительным КПД турбины

, (10.3)

эта величина обычно задается, исходя из опыта, и по ней определяют Δi_Т и параметры рабочего тела в точке «4».

Потери от необратимости в процессе сжатия рабочего тела в насосе (или в компрессоре) тоже приводят к повышению энтропии; реальный процесс идет не по изоэнтропе 1-2а, а по политропе 1-2. Работа сжатия в реальном процессе увеличивается и становится равной Δi_Н = i₂ – i₁. Разность i₂ –i_2а превращается в тепло трения. Отношение теоретической работы сжатия к действительной называется внутренним относительным КПД этого аппарата

, (10.4)

эта величина тоже задается, и по ней определяем Δi_Н и параметры рабочего тела после действительного сжатия, т.е. в точке «2».

Турбину и насос (или компрессор) условно считают основными источниками необратимости; учет этих необратимостей приводит к следующему показателю – внутреннему КПД цикла. Формулы для аналогичны формулам для (с заменой обратимых процессов на необратимые)

(10.5)

Отношение внутреннего КПД цикла к его термическому КПД называют внутренним относительным КПД цикла: .

Отсюда

, (10.6)

эта величина показывает, насколько действительный цикл менее совершенен, чем обратимый цикл (т.е. какую долю составляет внутренний КПД действительного цикла). Чтобы отличать от , величину иногда называют внутренним абсолютным КПД цикла.

Внутренний абсолютный КПД реального цикла еще не полностью характеризует эффективность ТЭУ. Работа, произведенная в цикле, не равна работе, переданной внешнему потребителю; часть произведенной работы необратимо расходуется в виде механических, тепловых и электрических потерь агрегатов. Величина потерь в каждом из элементов установки характеризуются величиной, так называемого эффективного КПД этого элемента . Перемножив между собой все эти КПД и внутренний абсолютный КПД цикла, получим эффективный абсолютный КПД всей теплоэнергетической установки в целом

, (10.7)

здесь – произведение величин эффективных КПД, характеризующих необратимые потери во всех n элементах установки. Эффективный КПД ТЭУ показывает, какая доля тепла q_под (введенного в установку при сгорании органического топлива или при делении ядерного горючего, или подведенного от какого-либо другого источника) превращена в работу, отданную внешнему потребителю (в ).

(10.8)

Для электростанции – это электроэнергия, отданная в энергосистему.

Обратим особое внимание на математическую тонкость при анализе циклов по формулам для КПД. Выражения (10.1; 10.5; 10.8) представляют формулы для КПД цикла с разной степенью приближения к реальности. Глядя на формулу для КПД цикла можно подумать, что при КПД цикла тем выше, чем меньше величина подводимого в цикле тепла. Но это не корректное суждение, поскольку q_под входит не только в знаменатель, но и в числитель ( ).

Если выдерживать (а это, в принципе, в определенных пределах возможно), то, исходя из вида формулы , получается обратная картина – КПД будет снижаться с уменьшением q_под (вплоть до q_под = q_отв, когда η_ц = 0, а дальше вообще бессмыслица η_ц  0). А истина заключается в том, что нельзя отдельно рассматривать части формулы. Следует обращать внимание и на q_под и на q_отв и помнить, что для получения работы в прямом цикле q_под должно быть больше q_отв, т.е. q_под  q_отв.

Эту математическую тонкость упустил из виду А.И. Андрющенко [10.2, с. 21], рассуждая о влиянии q_под на поведение термического КПД цикла. вот эти рассуждения. «В ряде случаев термический КПД не соответствует требованиям основного показателя эффективности термодинамических циклов. Действительно, если увеличивают q_под, то может оказаться, что достигаемая при этом работа , несмотря на ухудшение , тоже возрастает. В этих случаях для поиска оптимальных условий построения цикла надо находить новый, более пригодный для этой цели показатель». Здесь вид формулы увел автора от истины; он считает, что увеличение q_под должно ухудшать η_ц, забывая, что q_под входит и в числитель ( ). Т.е. на самом деле, возможны разные поведения , , (их рост, их уменьшение), и при этом η_ц может и расти и падать. Но при этом η_ц будет оставаться верным показателем термодинамической эффективности циклов ( – верный показатель совершенства обратимого цикла; – показатель эффективности цикла с учетом необратимых потерь в процессе расширения рабочего тела в турбине и в процессе его сжатия в насосе (компрессоре); – показатель оптимальности цикла установки в целом).

И еще одна тонкость кроется в определении понятия КПД цикла. В [10.2] дается несколько формулировок КПД цикла, на первый взгляд одинаковых, а на самом деле принципиально разных (и в других учебниках на этом не заостряют внимание).

Определение 1. Отношение полезной работы обратимого цикла к подведенной теплоте называют термическим КПД данного цикла: [10.2; с. 10].

Определение 2. Показателем совершенства рассматриваемого реального цикла, очевидно, является отношение действительной работы цикла к затраченной теплоте, называемое абсолютным внутренним или внутренним КПД цикла: [10.2; с. 17].

Определение 3. В качестве показателя эффективности прямого термодинамического цикла, предназначенного для выработки механической (электрической) энергии, выбирают такой коэффициент, максимум которого обеспечивает достижение наибольшей полезной работы цикла, отнесенной к единице расходуемой теплоты. Для полностью обратимых (идеальных) циклов таким показателем является термический КПД [10.2; с. 21].

Итак, три похожих формулировки КПД цикла, но есть нюанс. Первая формулировка термодинамически точная. Она берет на учет все подводимое извне тепло (не будем придираться к термину «теплота», употребляемого здесь вместо термина «тепло»). Дело в том, что подводимое в цикле тепло q_под может состоять из двух составляющих: тепло подводимое с затратами (на органическое или ядерное топливо) q_з и тепло, доставшееся почти бесплатно (от окружающей среды, недоиспользованное на каком-то производстве или бросовое) q_б, т.е. q_под = q_з + q_б. Если q_б буквально бесплатно, то с экономической точки зрения его можно не учитывать, принимать q_б = 0. И если пользоваться формулой , забыв, что , то уменьшение q_под на величину q_б вроде бы увеличит η_ц. На самом же деле, по формуле видно, что в зависимости еще и от q_отв η_ц может и увеличиться, и уменьшиться, и остаться неизменным. А с термодинамических позиций не имеет значения источник q_под (бросовый или с затратами), все q_под – подведенное в цикл извне, его следует учитывать полностью.

Понятия: «затраченное», «расходуемое» тепло (как в определениях 2 и 3); «недоиспользованное», «бросовое», «бесплатное» и т.п. – это категории экономические, а не термодинамические. Для термодинамики – это тепло, подводимое в цикл извне. Т.е., определения 2 и 3, толкующие понятие КПД с использованием экономических терминов, не точны и могут приводить к недоразумениям. Вероятно, недоучет этих терминологических и математических тонкостей приводят к тому, что иногда можно встретить в литературе (в том числе и в [10.2; с. 301]) утверждение о возможности величины КПД больше единицы. Подробнее об абсурдности такого утверждения изложено в работах [10.3; 10.4; 10.5].

Продолжение темы 10 (лабораторная работа № 5)

Разные способы повышения КПД цикла теплоэнергетических установок

Реферативное изложение

Зависимость термического КПД обратимого цикла Карно от верхней температуры цикла. Два пути повышения КПД цикла (выбор оптимальной конфигурации цикла и выбор параметров цикла).

Сравнительные расчеты: оценка термодинамического эффекта от введения промежуточного подогрева рабочего тела в процессе его расширения в турбине, промежуточного охлаждения в процессе его сжатия в компрессоре. Оценка термодинамического эффекта от перегрева пара в цикле Ренкина.

На стадии термодинамических исследований циклов и на их основе принципиальных тепловых схем теплоэнергетических установок, когда еще речь не идет о технико-экономической оптимизации ТЭУ, критерием эффективности служит КПД цикла (или термический или внутренний абсолютный , или эффективный абсолютный установки – в зависимости от стадии термодинамического исследования); чем выше значение КПД, тем цикл считается термодинамически совершеннее.

Поскольку на данной стадии практически нет ограничений, то такие (теоретические) расчеты могут приводить к величинам КПД близким к единице. Покажем это на изменении КПД обратимого цикла Карно (табл. 10.1). Пусть температура отвода тепла будет t_отв = 0 (Т_отв = 273 К), а температура подвода тепла изменяется в диапазоне t_под = 20  2000 (Т_под = 293  2273 К).

Таблица 10.1 – Зависимость КПД обратимого цикла Карно от верхней температуры цикла

293 373 773 1273 1773 2273	0,068 0,268 0,647 0,786 0,846 0,88

Не смотря на теоретическую раскрепощенность, мы все же взяли исходные данные в разумных пределах, т.е. не стали снижать Т_отв до нуля градусов по Кельвину и верхнюю температуру цикла ограничили 2000 . Т.е., у исследователя обычно есть опыт, и он не слишком отклоняется от технически допустимых величин в исходных данных.

Говоря о способах повышения КПД цикла, мы подразумеваем два пути: 1) выбор термодинамически оптимальной конфигурации цикла в T-S и i-s диаграммах и 2) выбор его параметров; что приводит к определенной структуре тепловой схемы ТЭУ, т.е. к соответствующему набору элементов схемы. Имея в виду формулу для термического КПД обратимого цикла Карно (идеального в теоретическом плане) , в общем случае понятно стремление к максимальной температуре подвода тепла и к минимальной температуре отвода тепла. Поскольку в паровой (газовой) области подвод тепла по изотерме невозможен (а в чисто газовом цикле и отвод тепла по изотерме невозможен), то под температурами подвода и отвода тепла понимают средние температуры. Под средней температурой подвода (отвода) тепла понимают температуру такого изотермического процесса, для которого подвод(отвод) тепла q_под (q_отв) приводит к такому же изменению энтропии, что и в действительном процессе. Графически это выглядит, как на рис. 10.2.

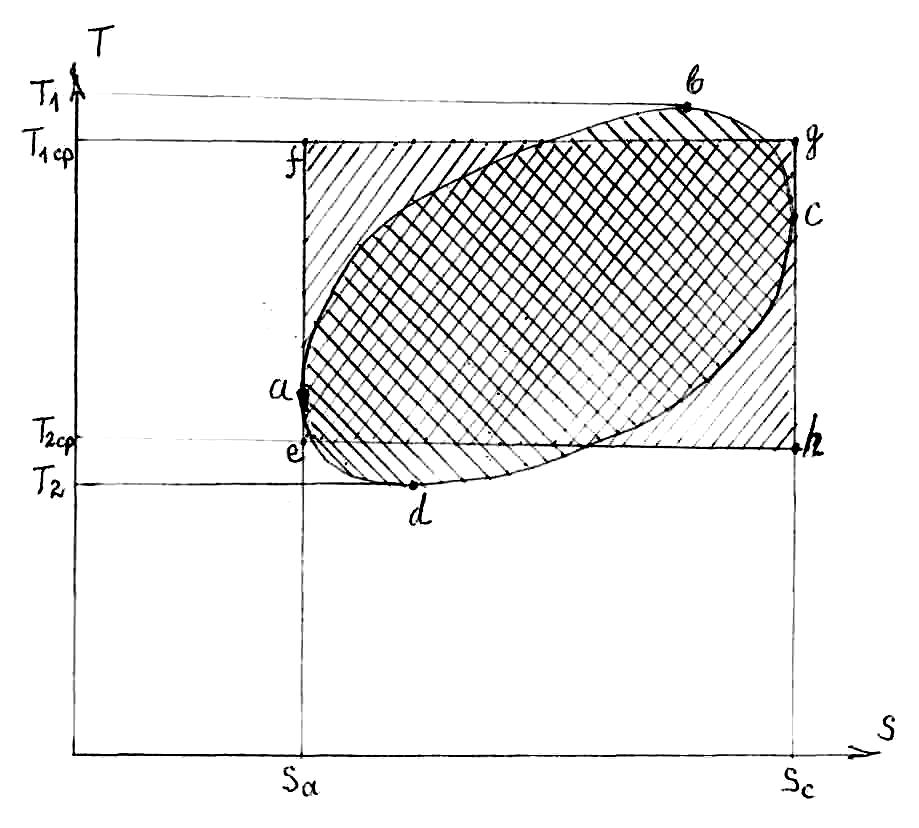
Рисунок 10.2 – T-S диаграмма произвольного обратимого цикла

(a-b-c-d-a) и равного ему (по величине термического КПД)

обратимого цикла Карно (e-f-g-h-e)

Математическая подоплека средних температур выглядит так. Тепло, подводимое к теплоносителю (рабочему телу) в произвольном цикле q_под изображается площадью S_a-a-b-c-S_c-S_a и определяется по формуле

. (10.9)

Отводимое тепло q_отв изображается площадью S_a-a-d-c-S_c-S_a, определяется

. (10.10)

Среднюю температуру подвода тепла определяем так

, (10.11)

а среднюю температуру отвода тепла – соотношением

. (10.12)

Из (10.9) и (10.11) находим, что

, (10.13)

а из (10.10) и (10.12) находим, что

(10.14)

Подставляя (10.13) и (10.14) в формулу для термического КПД , получаем следующее соотношение для термического КПД рассматриваемого произвольного обратимого цикла

(10.15)

Таким образом термический КПД произвольного обратимого цикла, осуществляемого в интервале температур от Т₁ до Т₂, равен по величине термическому КПД обратимого цикла Карно, осуществляемого в более узком интервале температур от Т_1ср до Т_2ср (см. рис. 10.2). Исходя из формул для средних температур (10.11 и 10.12) их иногда называют среднеинтегральными или еще – среднепланиметрическими.

Такого рода сведение расчета термического КПД любого произвольного обратимого цикла через формулу для термического КПД цикла Карно и вообще, «все способы повышения термического КПД цикла, связанные с приближением Т_1ср к Т_max и Т_2ср к Т_min, А.И. Андрющенко предпочитает называть карнотизацией циклов [10.2]. Термин этот довольно спорный и не всеми применяется; спорный хотя бы потому, что судить об эффективности цикла по величинам температур (подвода и отвода тепла) можно только в простейших тепловых схемах и на ранней стадии исследования. Например, регенерация тепла, отбираемого из паровой турбины не понижает температуру отводимого в конденсатор тепла, однако количество отводимого тепла уменьшается и это способствует повышению КПД цикла ( и термического в том числе).

Наиболее широко применяемые способы повышения КПД циклов теплоэнергетических установок следующие: регенерация, комбинирование циклов, ступенчатый подвод тепла и ступенчатый отвод тепла в цикле, выбор оптимальных параметров цикла.

Регенерацию (полнорасходную в газовом цикле и с отборами тепла из турбины в пароводяном цикле) мы рассматривали и убедились в ее эффективности.

Комбинирование в виде бинарного соединения газового цикла (верхнего) с пароводяным (нижним) циклом тоже рассмотрели, термодинамический эффект почувствовали.

Рассмотрим теперь ступенчатый подвод тепла в цикле в виде однократного промежуточного подогрева рабочего тела в процессе его расширения в турбине. Сравнительный расчет проведем для замкнутого воздушного регенеративного цикла без учета необратимых потерь (т.е. по термическому КПД цикла ), а затем с учетом необратимых потерь в турбине и в компрессоре (т.е. по внутреннему абсолютному КПД ) с теми же исходными данными, что и ранее. На рис. 10.3 показана принципиальная тепловая схема рассматриваемой ГТУ. Принцип работы ГТУ следующий.

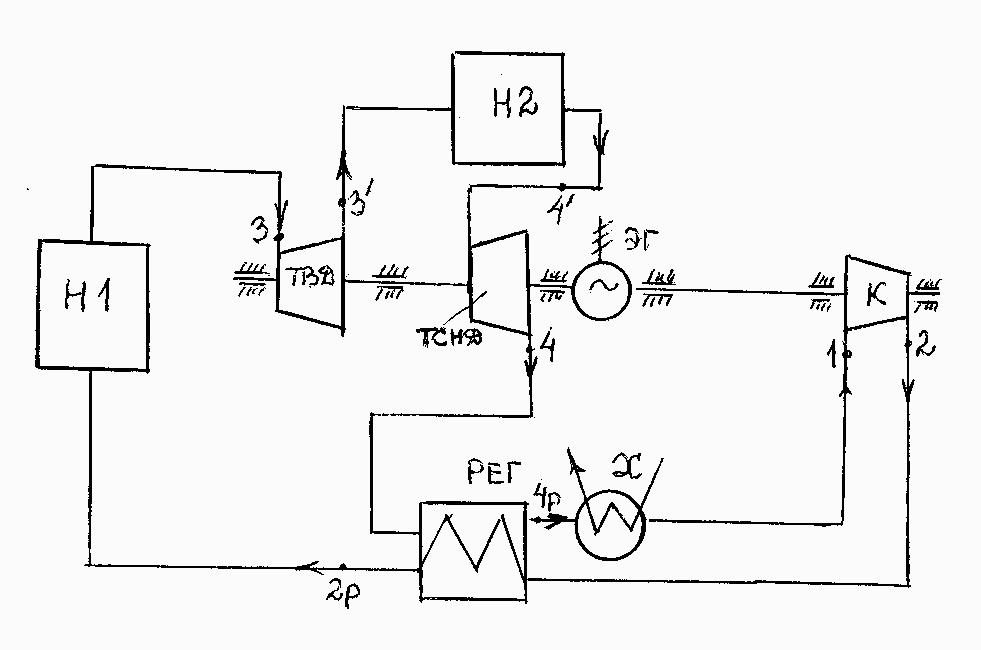
Рисунок 10.3 – Принципиальная тепловая схема ГТУ замкнутого

цикла с полнорасходной регенерацией и с однократным промежуточным подогревом теплоносителя – рабочего тела

Нагретый в нагревателе Н1 воздух при начальной температуре t₃ поступает в турбину высокого давления ТВД, где частично расширяется, совершая работу. Затем, при каком-то промежуточном давлении Р_3′, воздух направляется в нагреватель Н2 (или в тот же нагреватель Н1), где нагревается снова до начальной температуры (или до другой t_4′) и окончательно расширяется в турбине среднего и низкого давления ТСНД, опять же совершая работу. Разумеется, суммарная работа в ТВД и в ТСНД будет больше работы в цикле без промежуточного подогрева, что дает надежду на повышение КПД цикла. Дальнейший путь воздуха (регенератор, холодильник, компрессор, регенератор, нагреватель) такой же, как и в схеме без промежуточного подогрева.

На рисунке 10.4 изображена T-S диаграмма нового цикла в качественном виде. Для сравнения с предыдущими циклами на воздухе возьмем одинаковые исходные данные (Р₁, t₁, P₂, t₃, η_т, η_к). Р₁ = 1 бар; Т₁ = 290 К; i₁ = f(P₁, T₁) = 290 кДж/кг; S₁ = f(P₁, T₁) = 6,837 кДж/(кг·град). Р₂ = 10 бар; i_2а = f(P₂, S₁) = 562 кДж/кг; Т_2а = f(P₂, i_2а) ≈ 558 К; Δ i_ка = i_2а – i₁ = 272 кДж/кг; , кДж/кг; i₂ = i₁ + Δ i_к = 610 кДж/кг; Т₂ = 600 К.

Р₃ = 10 бар; Т₃ = 1400 К; i₃ = f(P₃, T₃) = 1516 кДж/кг; S₃ = f(P₃, T₃) = 7,87 кДж/(кг·град). Пусть промежуточное давление в турбине Р_3′ = 6 бар; i_3′а = f(P_3′, S₃) = 1327 кДж/кг; = i₃ – i_3′а = 1516 – 1327 = 189 кДж/кг; ; Δi_твд = ∙ = 164,4 кДж/кг; i_3′ = i₃ – Δi_твд = 1516 – 164,4 = 1351,6 кДж/кг; Т_3′ = f(P_3′, i_3′) ≈ 1261 К.

Температуру промподогрева (на входе в ТСНД) принимаем равной температуре на входе в ТВД Т_4′ = Т₃ = 1400 К; i_4′ = f(P_3′, T_4′) ≈ 1516 кДж/кг; S_4′ = f(P_3′, T_4′) = 8,01 кДж/(кг·град); i_4а = f(P₁, S_4′) =926 кДж/кг; Т_4а = f(P₄, i_4а) = 893 К; = i_4′ – i_4а = 590 кДж/кг; ; Δi_тснд = ∙ = 513,3 кДж/кг; i₄ = i_4′ – Δi_тснд = 1516 – 513,3 = 1002,7 кДж/кг; Т₄ = f(P₄, i₄) = 960 К.

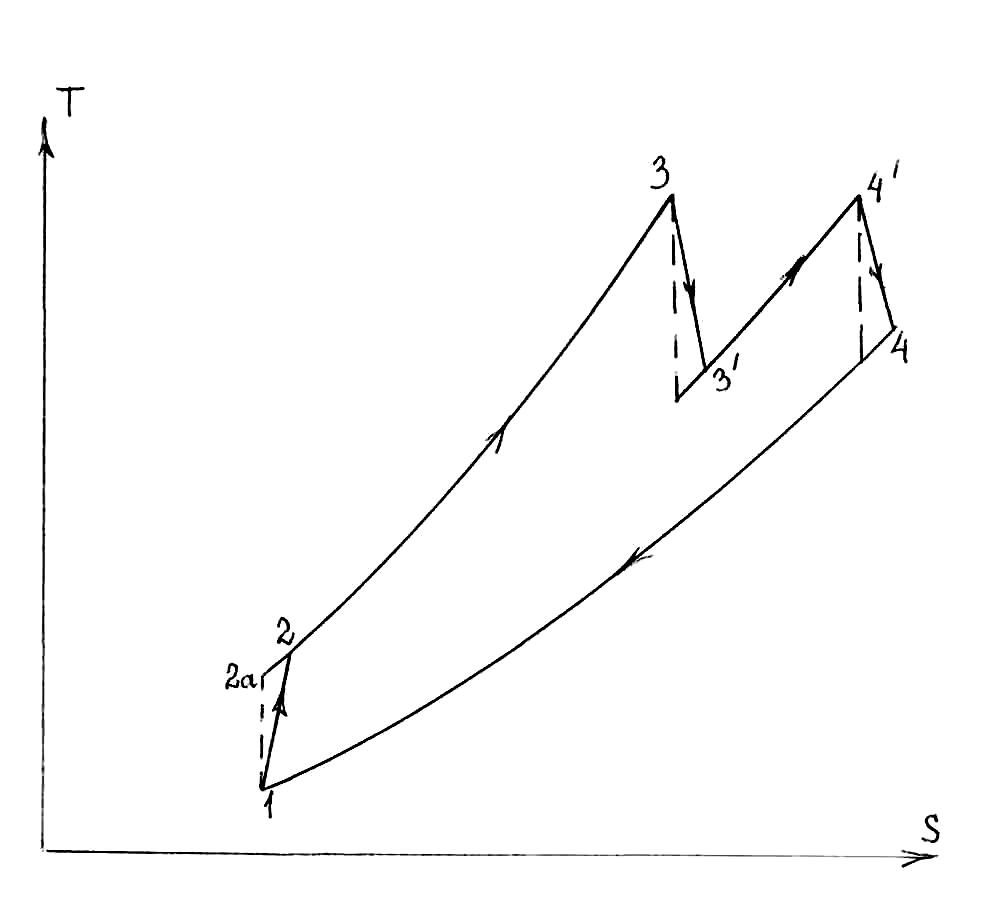
Рисунок 10.4 – T-S диаграмма газового цикла с промежуточным

нагревом и с регенерацией

Как и при расчете регенеративного воздушного цикла (в теме 9) принимаем минимальный температурный напор в регенераторе равным и предполагаем, что он находится на горячем конце регенератора, т.е. Т_2ра = Т_4а = 893 К. i_2ра = f(P₃, T_2ра) = 926 кДж/кг; i_4ра = i_4а – (i_2ра – i_2а) = 926 – (926 – 562) = 562 кДж/кг; Т_4ра = f(P_4р, i_4ра) ≈ 558 К = Т_2а. Снова получили эквидистантность кривых 4а-4ра и 2ра-2а (в t-N диаграмме; тогда как в T-S диаграмме эти кривые явно не эквидистантны). i_2р = i₄ = 1002,7 кДж/кг; Т_2р = Т₄ = 960 К.

Величина термического КПД обратимого цикла с промподогревом и регенерацией находится по такой формуле

(а без промподогрева η_т = 0,615). Эффект от ввода промподогрева по величине термического КПД составил Δη_т = 0,651 – 0,615 = 0,036 или 3,6% абсолютных. Это существенная термодинамическая добавка. Относительное увеличение .

Внутренний КПД цикла

.

Относительный прирост

.

Рассмотрим ступенчатый отвод тепла в цикле в виде однократного промежуточного охлаждения воздуха в процессе его сжатия в компрессоре. Схема ГТУ в измененном виде представлена на рис. 10.5, а на рис. 10.6 изображен цикл этой установки в T-S диаграмме. Здесь изменения коснулись процесса сжатия рабочего тела; один компрессор заменен двумя, с промежуточным охлаждением рабочего тела в дополнительном холодильнике Х2.

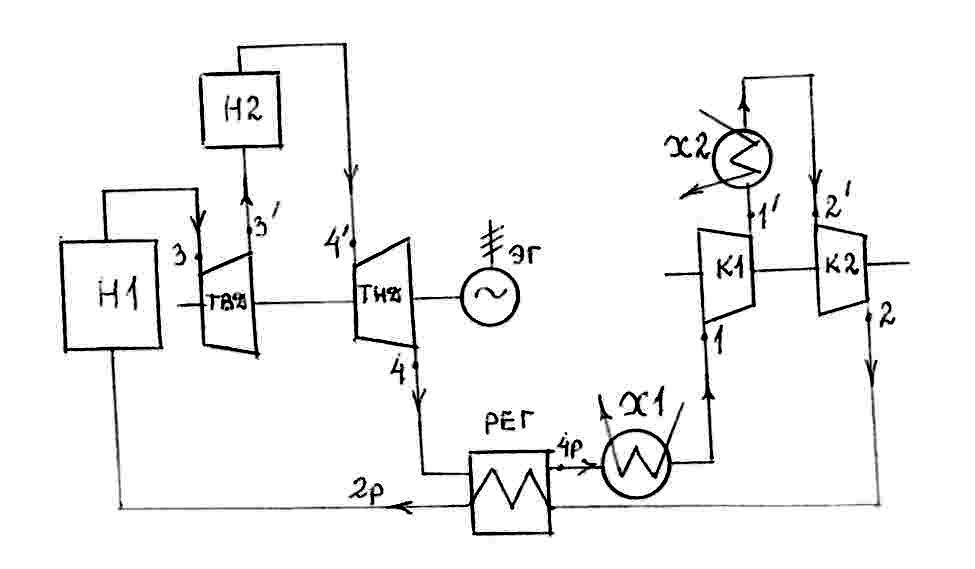
Рисунок 10.5 – Принципиальная тепловая схема ГТУ замкнутого цикла с регенерацией, однократным промнагревом и однократным промохлаждением рабочего тела

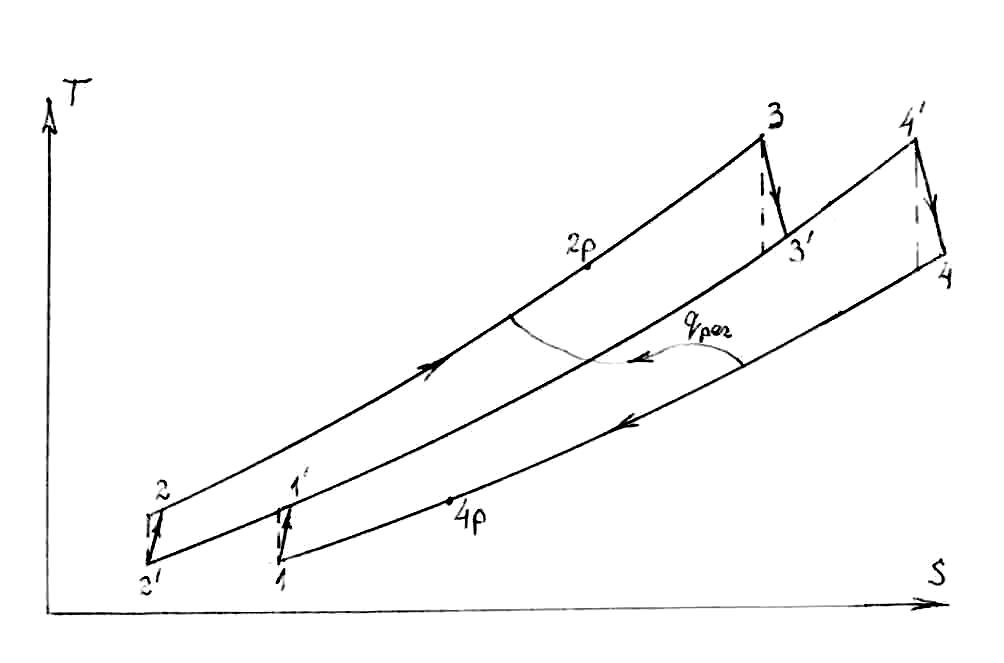
Рисунок 10.6 – T-S диаграмма газового цикла с регенерацией, с промнагревом и промохлаждением

Р₁ = 1 бар; Т₁ = 290 К; i₁ = 290кДж/кг; S₁ = 6,837 кДж/(кг∙град). Пусть промежуточное давление между компрессорами К1 и К2 Р_1′ = 3 бар, тогда i_1′a = f(P_1′, S₁) = 397 кДж/кг; = i_1′a – i₁ = 397 – 290 = 107 кДж/кг; ; кДж/кг; i_1′ = i₁ + Δ i_К1 = 290 + 125,9 = 415,9 кДж/кг; Т_1′ = f(P_1′, i_1′) ≈ 415,4 К.

Т_2′ = Т₁ = 290 К; i_2′ = f(P_1′, Т_2′) = 290 кДж/кг; S_2′ = f(P_1′, Т_2′) = 6,522 кДж/(кг∙град); Р₂ = 10 бар; i_2а = f(P₂, S_2′) = 410 кДж/кг; = i_2a – i_2′ = 410 – 290 = 120 кДж/кг; кДж/кг; i₂ = i_2′ + Δ i_К2 = 290 + 141,2 = 431,2 кДж/кг; Т₂ = f(P₂, i₂) = 431 К.

Т_2ра = Т_4а = 893 К; i_2рa = f(P₃, Т_2ра) = 926 кДж/кг; i_4рa = i_4а – (i_2рa – i_2a) = 926 – (926 – 410) = 410 кДж/кг; Т_4ра ≈ 410 К = Т_2а. Т_2р = Т₄ = 960 К; i_2р = i₄ = 1002,7 кДж/кг; i_4р = i₄ – (i_2р – i₂) = 1002,7 – (1002,7 – 431,2) = 431,2 кДж/кг; Т_4р ≈ 431 К = Т₂.

Находим термический КПД обратимого цикла

(без промохлаждения η_т = 0,651).

Внутренний абсолютный КПД цикла

(без промохлаждения ).

Рассматривая пароводяные циклы (Карно, Ренкина, в бинарной комбинации с надстройкой воздушного цикла, без регенерации и с регенерацией), мы везде брали турбину на насыщенном паре, т.е. на входе в турбину задавали температуру на правой ветви линии насыщения; а конкретно задавали , что соответствовало сопряженному давлению . (Параметры Р, t на линии насыщения иногда называют сопряженными). Расширяясь до давления ( ) водяной пар становился слишком влажным (степень сухости х ≈ 0,65), влажность 35% недопустима для нормальной работы лопаток турбины. В предыдущих теоретических расчетах нас это не смущало. Забегая вперед, заметим, что допустимой максимальной влажностью водяного пара считается  13%.

Влажность пара на выхлопе турбины можно уменьшить перегревом пара на входе в турбину. Оценим термодинамический эффект от перегрева пара в паротурбинной установке (ПТУ). Схема с перегревом пара в цикле Ренкина внешне (структурно) выглядит так же, как на рис 9.3. Пусть по той же изобаре Р₃ = 16,54 МПа пар перегревается до температуры t₃ = 565 (такая температура характерна для мощных паротурбинных энергоблоков на тепловых электростанциях (ТЭС)). i₃ = f(P₃, t₃) = 3470 кДж/кг; S₃ = f(P₃, t₃) = 6,502 кДж/(кг∙град). Р₄ = 0,0032 МПа; t₄ = 25 ; i_4a = f(P₄, S₃) = 1930 кДж/кг. = i₃ – i_4а = 3470 – 1930 = 1540 кДж/кг; = 0,87; Δi_Т = ∙ = 1339,8 кДж/кг; i₄ = i₃ – Δi_Т = 2130,2 кДж/кг. Степень сухости пара на выхлопе из турбины х = f(P₄, i₄) = 0,82 (82%). Влажность пара на выхлопе турбины (100 – 82 = 18%) снизилась. Дальнейшее понижение влажности можно достичь разными путями:

1. снижением давления пара на входе в турбину;

2. введением промежуточного перегрева пара в процессе его расширения в турбине.

Каков же термодинамический эффект от перегрева пара до t₃ = 565 ? Пусть регенеративный отбор пара из турбины осуществляется на средине изоэнтропного теплоперепада, т.е. кДж/кг, тогда параметры пара в отборе такие: кДж/кг; Р₀₁ = f(S₃, ) = 8 бар = 0,8 МПа. Изоэнтропный (адиабатический) теплоперепад в части высокого давления (ЧВД) турбины (от начала расширения пара до регенеративного отбора) кДж/кг; действительный теплоперепад ЧВД кДж/кг. Параметры пара в отборе такие: i₀₁ = i₃ – Δi_ЧВД = 3470 – 669,9 =2800,1 кДж/кг; t₀₁ = f(P₀₁, i₀₁) = 186 , это еще перегретый пар, и t-N диаграмма передачи тепла в регенераторе будет существенно отличаться (см. рисунок 10.7 и сравните с рисунком 9.4).

Температура пара на линии насыщения (начало конденсации в регенераторе = f(P₀₁) = 170,4 ; окончание конденсации – индекс ) = f(P₀₁) = 2768,4 кДж/кг.

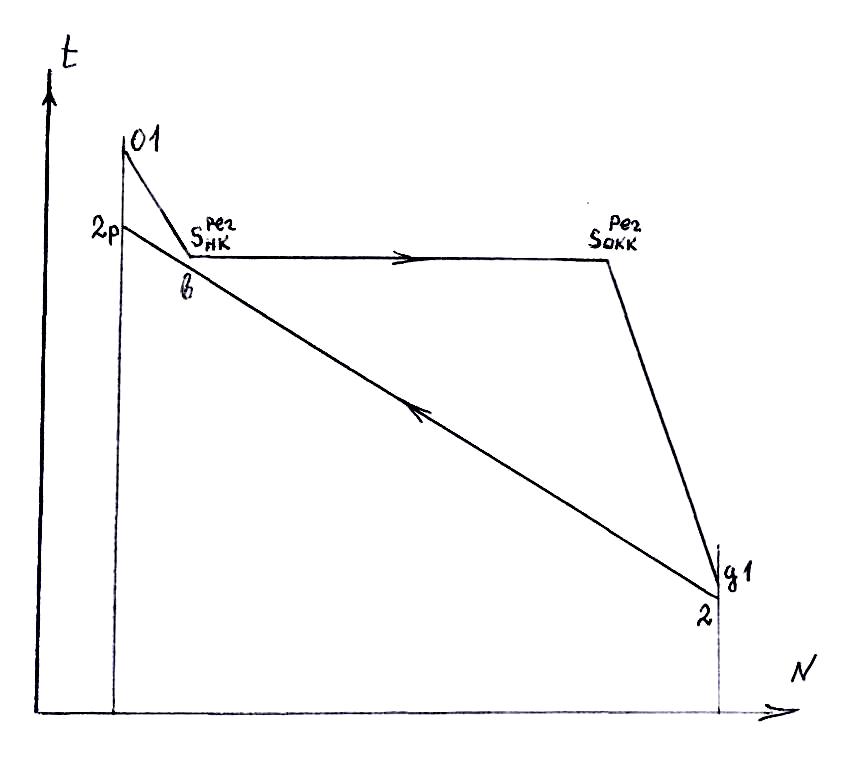
Рисунок 10.7 – t-N диаграмма передачи тепла в регенераторе

в цикле с перегревом пара

Температура дренажа (это из предыдущего расчета); Р_д1 = P₀₁ = 8 бар; кДж/кг; температура воды в сечении, где температурный напор между греющим паром и обогреваемой водой , . Давление принимаем по всему тракту одинаковым Р_в = Р₃ = 16,54 МПа; i_в = f(P_в, t_в) = 729,7 кДж/кг; i₁ = 104,7 кДж/кг.

Работа сжатия воды в насосе в адиабатическом процессе (Р₂ – Р₁) ∙ ν ∙ 10³ = (16,54 – 0,003) ∙ 0,001 ∙ 10³ = 16,54 кДж/кг; 104,7 + 16,5 = 121,2 кДж/кг; . Работа сжатия воды в насосе в действительности (в политропном процессе) 16,54/0,8 = 20,68 кДж/кг; i₂ = i₁ + Δi_н = 104,7 + 20,7 = 125,4 кДж/кг; t₂ = f(P₂, i₂) = 26,3 ; t_д1 = t₂ = 26,3 ; i_д1 = f(P_д1, t_д1) = 110,9 кДж/кг.

На участке регенератора, где происходит конденсация пара и охлаждение воды (см. рис. 10.7) известны параметры во всех четырех концевых точках, и это дает возможность определить относительный расход пара в отборе из баланса мощностей на этом участке. В обратимом цикле баланс мощностей для этого участка выглядит так:

, отсюда (10.16)

.

Параметры питательной воды в обратимом цикле находим из баланса мощностей для всего теплообменника

(10.17)

121,2 + 0,2303 ∙ (2700 – 126,4) = 713,9 кДж/кг; .

Термический КПД обратимого цикла находим по формуле (9.7)

.

Вспомним, что в цикле без перегрева пара величина термического КПД была 0,45.

А теперь учтем необратимости процессов в турбине и насосе и найдем величину внутреннего абсолютного КПД цикла .

Относительный расход пара в отборе

Параметры питательной воды в «реальном» цикле

i_2p = i₂ + α₀₁ ∙ (i₀₁ – i_д1) = 125,4 + 0,2274 ∙ (2800,1 – 110,9) = 736,9 кДж/кг;

t_2p = f(P_2p, i_2p) = 172,1 ;

.