[Править]умо относительно σ-алгебры

Случайная величина   называется условным математическим ожиданием   относительно σ-алгебры  , если

•  измерима относительно  .

• ,

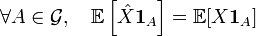где   — индикатор события  . Условное математическое ожидание обозначается  .

Пример. Пусть   Положим  . Тогда   — σ-алгебра, и  . Пусть случайная величина   имеет вид

.

Тогда

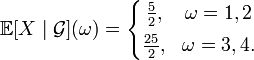
Умо относительно семейства событий

Пусть   — произвольное семейство событий. Тогда условным математическим ожиданием   относительно   называется

,

где   — минимальная сигма-алгебра, содержащая  .

Пример. Пусть   Пусть также  . Тогда  . Пусть случайная величина   имеет вид

.

Тогда

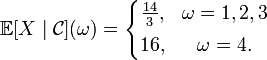
Умо относительно случайной величины

Пусть   другая случайная величина. Тогда условным математическим ожиданием   относительно   называется

,

где   — σ-алгебра, порождённая случайной величиной  .

Другое определение УМО   относительно  :

Такое определение конструктивно описывает алгоритм нахождения УМО:

• найти математическое ожидание случайной величины  , принимая   за константу  ;

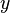• Затем в полученном выражении   обратно заменить на случайную величину  .

Пример: 

Условная вероятность

Пусть   — произвольное событие, и   — его индикатор. Тогда условной вероятностью   относительно   называется

.

37

Числовые характеристики системы случайных величин.

 

В основе рассмотрения числовых характеристик лежит понятие моменты.

 

Начальный момент   порядка k+S определяется след. образом:

Они определяют центр возможных значений системы (X,Y).

 

Центральный момент   порядка k+S определяется след. образом:

-смешанный центр. момент 2-го порядка =  .

-ковариационный момент

сov-ковариация

 

 и  описывают разброс значений системы (X,Y) от центра, соотв. вдоль осей Ox и Oy.   характериз. связь между переменными X и Y.

 

Математ. ожидания, дисперсии и моменты, составляющих систему СВ можно выразить через их законы распределения или через закон распределения самой системы.

 

M(X)=

 

Условный закон распред. составляющих.

Условные числовые характеристики: условное математ. ожидание и условную дисперсию.

 (2)

f(x)-функция регрессии, график этой функции-линией регрессии.

Корреляционный момент и коэффициент корреляции.

Для описания системы двух случайных величин, кроме математических ожиданий и дисперсий составляющих, пользуются и другими характеристиками, к числу которых относятся корреляционный момент и коэффициент корреляции.

Коррелщионным_мотнтом   случайных величин X и Y называют математическое ожидание произведения отклонений этих величин: 

Теорема. Корреляционный момент двух независимых случайных величин X и Y равен нулю.

Доказательство. Так как X и Y независимые случайные величины, то их отклонения X—М(Х) и Y—M(Y) также независимы. Пользуясь свойствами математического ожидания (математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий сомножителей) и отклонения (математическое ожидание отклонения равно нулю), получим

Из определения корреляционного момента следует, что он имеет размерность, равную произведению размерностей величин X и Y. Другими словами, величина корреляционного момента зависит от единиц измерения случай- случайных величин.

Такая особенность корреляционного момента является недостатком этой числовой характеристики, поскольку сравнение корреляционных моментов различных систем случайных величин становится затруднительным. Для того чтобы устранить этот недостаток, вводят новую числовую характеристику — коэффициент корреляции.

Коэффициентом корреляции -  случайных величин X и Y называют отношение корреляционного момента к произведению средних квадратнческих отклонений этих величин:

 

Очевидно, коэффициент корреляции независимых случайных величии равен нулю

38