6.3. Динамика фрикционного сцепления

Фрикционное сцепление является объектом регулирования, и поэтому его характеристики во многом определяют качество работы системы. На рис.б.5 приведена расчетная схема постоянно-замкнутого сцепления.

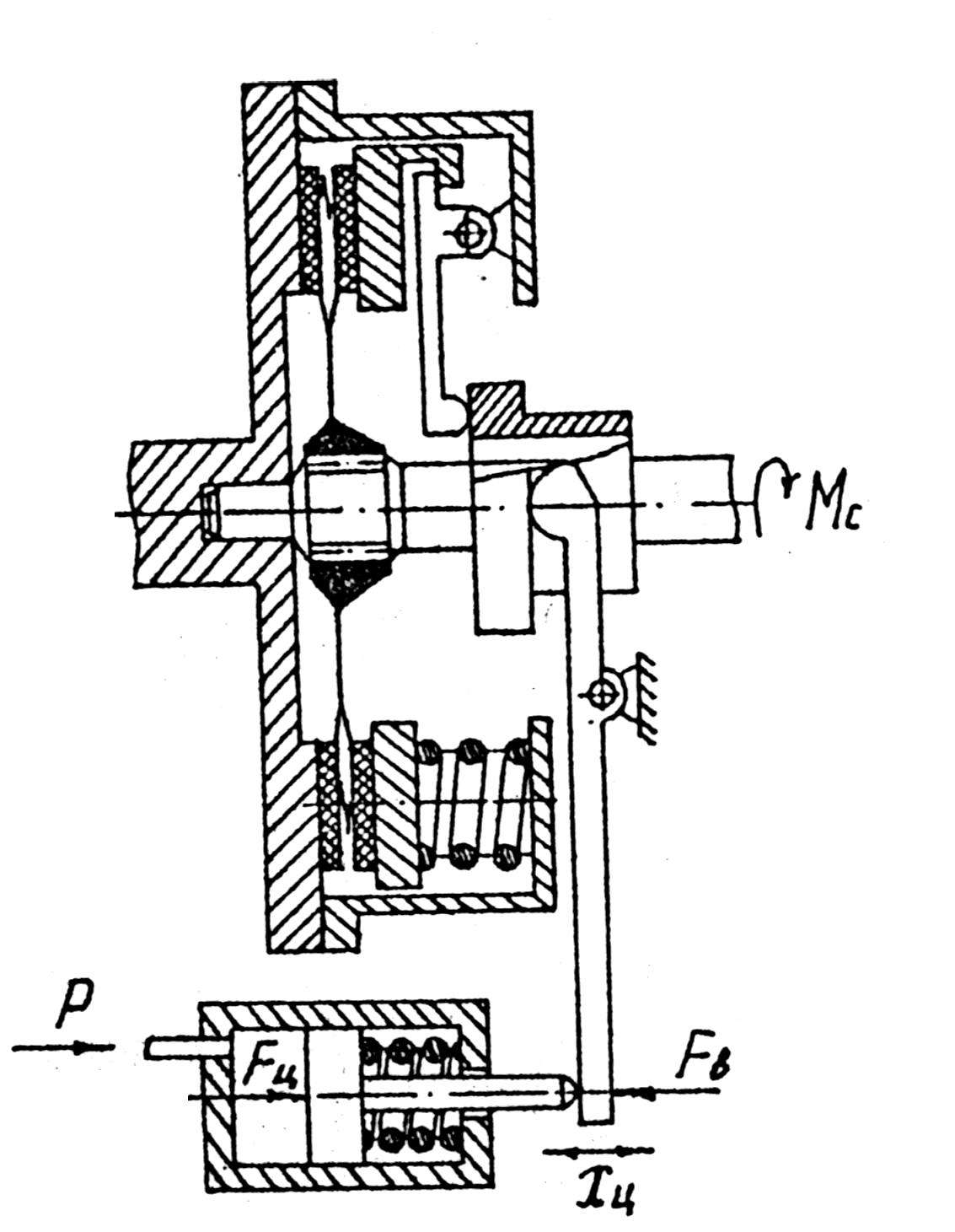
а

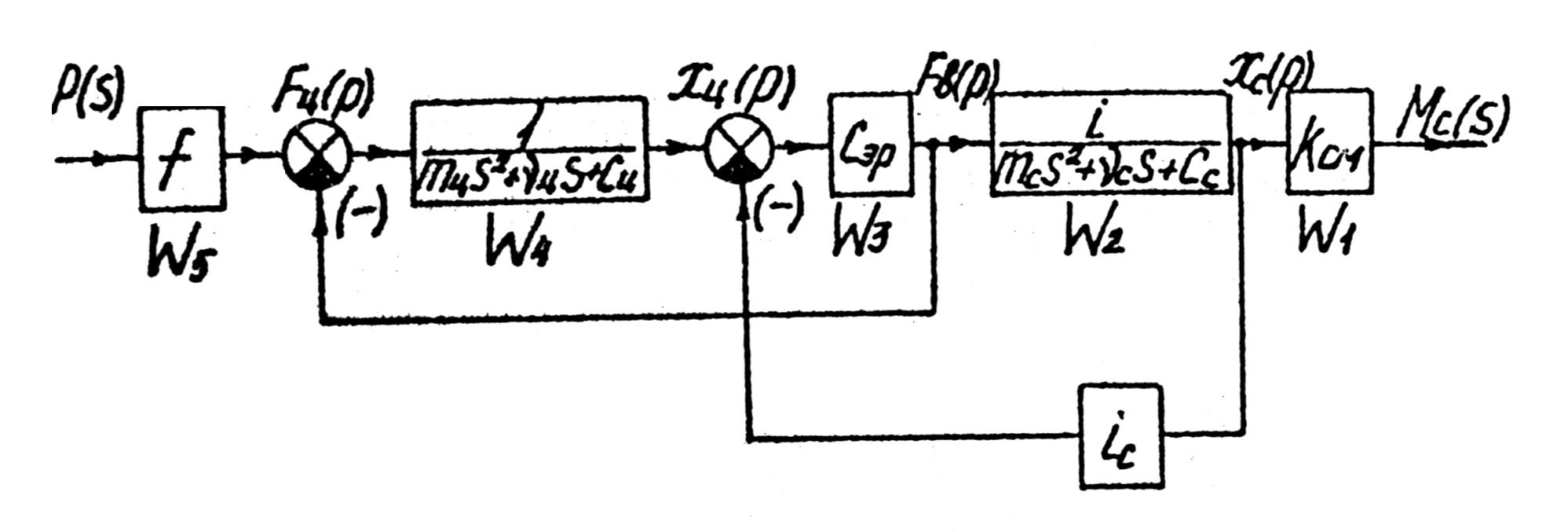
б

Рис 6.5. Расчетная (а) и структурная (б) схемы муфты сцепления.

Допускаем, что жесткость ведомого диска в осевом направ­лении является линейной функцией от осевой деформации диска. Будем определять передаточную функцию рассматриваемой системы в виде

W(s) = M_c (s)/p(s) (6.8)

Здесь M_c(s) - изображение выходного параметра (момента трения сцепления, a p(s) - изображение входного параметра (давление в исполнительном цилиндре). Для того, чтобы получить передаточную функцию системы необходимо составить структурную схему (рис.б.З:).

На структурной схеме обозначены следующие передаточные функции:

W₁ = M_c(s) /X_c(s) = K_cm (6.9)

где Х_c - деформация ведомого диска. M_c - момент трения сцепления.

К_cm - коэффициент усиления сцепления по моменту (К_cm = у R С_b), С_b - жесткость ведомого диска при его деформации, у - коэффициент трения накладок ведомого диска, R - средний радиус поверхности трения.

W₂ = X_c(s)/F_b(s) = i/(m_cs² + v_cs +C_b + C_m (6.10)

где F_b - сила, приложенная к концу вилки выключения сцепления,

i - коэффициент усиления сцепления по силе,

m_c - эквивалентная масса подвижных частей, приведенная к

нажимному диску,

v_c - коэффициент вязкого трения в механизме выключения,

С_m - жесткость нажимных пружин.

W₃ = F_b(s)/(X_u(s) – X_c(s)I_c) = C_3p (6.11)

где- X_u - перемещение штока сервоцилиндра.

C_3p-эквивалентная жесткость вилки, рычагов и т.д.

(6.12)

W₄ = X_u(s) / (F_u(s) – F_b(s)) = 1/(m_us² + v_us +c_u) (6.12)

где F_u - сила на поршне сервоцилиндра от давления жидкости,

m_u - масса подвижных частей сервоцилиндра,

v_u - коэффициент вязкого трения в сервоцилиндре,

c_u - жесткость возвратной пружины сервоцилиндра.

W₅ = F_u(s) /p(s) = f (6.13)

где f - площадь поршня исполнительного цилиндра.

Выполнив эквивалентные преобразования полученной структурной схемы, легко получить передаточную функцию системы "исполнительный цилиндр - фрикционное сцепление", которую и необходимо учитывать при анализе динамических свойств автоматизированного сцепления в целом.

Анализ показывает, что для улучшения динамических свойств необходимо по возможности уменьшать массы подвижных частей исполнительного цилиндра и увеличивать жесткость возвратной пружины.