20. Поняття про чотиривимірний простір Мінковського. Чотиривимірні вектори і тензори. Кованіантна форма запису фізичних законів.

Як уже відмічалося, проміжки часу та відстані не є інваріантами перетворень Лоренца. Замість цих двох величин найважливішим інваріантом в теорії відносності є величина, яка називається інтервалом.

Подія, що відбувається з будь-якою частинкою, характеризується місцем, де вона відбулася, і часом, коли вона відбулася. Нехай перша подія полягає в тому, що з точки, яка має координати в системі К в момент часу відправляється сигнал, що поширюється з швидкістю світла. Другою подією вважатимемо надходження сигналу в точку з координатами в момент часу . Тоді

. (19.16)

Інтервалом між двома подіями називають величину , яка визначається рівністю

. (19.17)

Для двох нескінченно близьких подій інтервал визначається виразом

. (19.18)

Внаслідок сталості швидкості поширення світла рівність (19.16) повинна виконуватись у будь-якій інерціальній системі відліку. Таким чином, якщо інтервал рівний нулю в системі К, то він буде рівним нулю і в довільній іншій системі К. Звідси слідує, що інтервали між подіями в системах К і К повинні бути пов’язані співвідношенням

,

причому коефіцієнт може залежати тільки від абсолютної величини відносної швидкості обох інерціальних систем відліку. В силу повної рівноправності систем К і К на тих же підставах можна записати, що

.

Перемноживши дві останні рівності, знаходимо, що , звідки . Природно припустити, що знак інтервалу в усіх системах відліку повинен бути однаковим. Таким чином, приходимо до висновку, що інтервал між двома подіями є інваріантом:

, (19.19)

причому з рівності нескінченно малих інтервалів слідує і рівність скінченних інтервалів.

Для координат двох подій в деякій системі К введемо позначення

.

Тоді квадрат інтервалу між цими подіями запишеться у вигляді

.

В будь-якій іншій інерціальній системі К для тих же подій

,

причому в силу інваріантності

. (19.20)

Припустимо, що , тобто інтервал дійсний. Тоді можна знайти таку систему відліку К, в якій , тобто події відбуваються одночасно. Відстань між точками, в яких відбулися події в системі К, згідно (19.20) рівна

. (19.21)

Дійсні інтервали називаються просторовоподібними.

Нехай тепер , тобто інтервал уявний. Тоді можна знайти таку систему К, в якій , тобто події, розділені інтервалом відбудуться в одній точці. Проміжок часу між подіями в системі К рівний

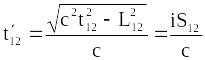. (19.22)

Уявні інтервали називаються часоподібними.

Події, що відбуваються з однією й тією ж частинкою, можуть бути розділені тільки часоподібним інтервалом. Дійсно, оскільки частинка не може рухатися з швидкістю, більшою , то пройдена нею за час відстань не може перевищити , тобто

звідки .

Просторово подібним інтервалом можуть бути розділені лише причинно не зв’язані події. Дійсно, якщо , то . Це означає, що жоден сигнал, який вийшов з одної точки простору, не може досягти за час другої точки і вплинути на подію, що відбувається в цій точці.

Все вище сказане справедливе і для нескінченно малих інтервалів. При цьому з інварантності просторово-часового інтервалу слідує інваріантність власного часу (19.13). Дійсно, оскільки

,

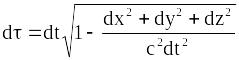то, враховуючи співвідношення (19.18), отримаємо

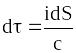. (19.23)

Розділення інтервалів на часоподібні та просторовоподібні в силу їх інваріантності є абсолютним, тобто не залежить від системи відліку. Введемо позначення

.

Сукупність величин зручно трактувати як декартові компоненти деякого вектора в чотиривимірному просторі-часі, який називається простором Мінковського.

Візьмемо деяку подію О за початок відліку часу і просторових координат. Для наочності розглядатимемо тільки часову і одну просторову координати, відкладаючи їх на двох осях. Прямолінійний рівномірний рух частинки, яка проходить через точку при , зобразиться прямою, що проходить через О і нахилена до осі часу від кутом, тангенс якого рівний швидкості частинки. Оскільки найбільша можлива швидкість рівна , то існує найбільший кут, який може утворювати ця пряма з віссю часу. На рис. 19.2 зображені дві прямі, які відповідають поширенню двох сигналів (з швидкістю світла) у протилежних напрямках, що проходять через подію О. Всі лінії, які зображають рухи частинок, можуть лежати тільки всередині областей aOc і dOb. На прямих ab і cd . Розглянемо спочатку події, світові точки яких лежать всередині області аОс. В усіх точках цієї області , тобто інтервали між будь-якою подією в цій області та подією О – часоподібні. Оскільки при цьому , то всі події в області аОс відбуваються після події О. Але дві події, розділені часоподібним інтервалом, в жодній системі не можуть відбутися одночасно. Значить, не можна вибрати ніякої системи відліку, де яка-небудь з подій області аОс відбулася б до події О. Таким чином, всі події області аОс є абсолютно майбутніми по відношенню до О, причому в усіх системах відліку.

Аналогічно, всі події області dOb є абсолютно минулими по відношенню до О.

Інтервал між довільною подією областей aOd і bOc та подією О – просторовоподібний. В будь-якій системі відліку ці події відбуваються в різних точках простору. Тому вказані області називаються абсолютно віддаленими по відношенню до події О. Однак поняття одночасності для цих подій відносні. Для будь-якої події областей aOd і bOc є такі системи відліку, де вона відбувається раніше чи пізніше події О і, нарешті, існує одна система відліку, де подія відбувається одночасно з О.

Якщо розглядати всі три просторові координати, то замість двох прямих, які перетинаються на рис. 19.2, ми отримали б конус , вісь якого співпадає з віссю часу (його називають “світовим конусом”). Області “абсолютно майбутнього“ та абсолютно минулого” зобразяться тоді відповідно двома внутрішніми порожнинами цього конуса.

1