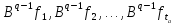- •5. Операторы простой структуры. (Диагонализуемость линейного оператора.) Критерий диагонализуемости линейного оператора.
- •6. Треугольная форма матрицы линейного оператора.
- •7. Нильпотентный оператор.
- •8. Корневые векторы и их простейшие свойства. Корневые подпространства.
- •9. Канонический базис корневого подпространства. Матрица оператора в каноническом базисе.
- •10. Жорданов базис и жорданова нормальная форма оператора.
- •11. Многочлен от линейного оператора. Теорема Гамильтона – Кэли.
- •12. Функции от матриц (линейных операторов).
- •13. Инвариантные подпространства минимальной размерности.
9. Канонический базис корневого подпространства. Матрица оператора в каноническом базисе.
 -
корневое подпространство
-
корневое подпространство
 ,
отвечающее собственному значению
,
отвечающее собственному значению .
.
 (сдвиг
оператора)
(сдвиг
оператора)
 .
.
Построим
корневое подпространство
 .
.
Надо
найти то
 ,
начиная с которого
,
начиная с которого ,
при этом:
,
при этом: =
алгебраическая кратность
=
алгебраическая кратность
Строим
базис
 ,
последовательно просматривая
подпространства
,
последовательно просматривая
подпространства (в обратном порядке).
(в обратном порядке).
До
 :
: - векторы, дополняющие базис
- векторы, дополняющие базис до
до :
:
1)
 – корневые, высоты
– корневые, высоты ,
т.к.
,
т.к. ;
;
2)
количество
 ;
;
3)
 ,
т.к.
,
т.к.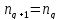 ;
;
4)
никакая линейная комбинация  не
принадлежит
не
принадлежит .
Такие векторы называются линейно
независимыми над
.
Такие векторы называются линейно
независимыми над .
.
До
 :
Построим
:
Построим -
корневые, высоты
-
корневые, высоты ,
- линейно независимы над
,
- линейно независимы над .
Дополним эти векторы векторами
.
Дополним эти векторы векторами так, чтобы вектора
так, чтобы вектора дополняли произвольный базис
дополняли произвольный базис до базиса
до базиса
1)
они корневые высоты
 ;
;
2)
их количество
 ;
;
3)
 ;
;
4)
они линейно независимы над
 .
.
До
 :
Аналогично:
:
Аналогично: -
корневые, высоты
-
корневые, высоты .
.
Выполняя
далее такие же построения в
 доходим до
доходим до .
.
До
 :
:
 -
дополяют до базиса
-
дополяют до базиса
 :
:
1) корневые высоты 1 – собственные;
2)
их количество
 ;
;
3)
 ;
;
4) они линейно независимы.
Полученную
за
 шагов систему векторов удобно объединить
в таблицу, которую будем называть
жордановой лестницей:
шагов систему векторов удобно объединить
в таблицу, которую будем называть
жордановой лестницей:
|
|
|
|
|
|
|
|
| |||
|
|
| |||
|
|
|
| ||
|
|
|
| ||
|
|
| |||
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |||
Теорема
9.1
Построенная система векторов образует
базис корневого подпространства
 .
.
∎ а) количество векторов в системе:

б) система векторов
линейно независима. От противного.
Рассмотрим линейную комбинацию векторов
и применим последовательно
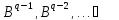
 ,
где
,
где
 -
корневые высоты
-
корневые высоты
 ,
остальные слагаемые равны нулю, т.к. они
корневые векторы высоты
,
остальные слагаемые равны нулю, т.к. они
корневые векторы высоты ,
следовательно,
,
следовательно, ,
в силу линейной независимости
,
в силу линейной независимости .∎
.∎
Нумерация базиса: по столбцам жордановой клетки снизу вверх, сами столбцы в произвольном порядке.
Полученный таким
образом базис называется каноническим
(или жордановым) базисом корневого
подпространства
 .
.
1) Пусть
 - векторы первого столбца жордановой
лестницы.
- векторы первого столбца жордановой
лестницы.
 ⟹
⟹ ⟹
⟹ ⟹
⟹ .
.
Этой группе
канонического базиса соответствуют
первые
 столбцов матрицы
столбцов матрицы в каноническом базисе, которые имеют
вид:
в каноническом базисе, которые имеют
вид:
 .
.
 –жорданова клетка.
–жорданова клетка.
Аналогично для
второго столбца жордановой лестницы:
диагональная клетка имеет тот же вид
 ,
остальные элементы равны нулю.
,
остальные элементы равны нулю.
Число таких клеток
 .
.
2) Следующая группа
из
 столбцов жордановой лестницы определяет
клетки
столбцов жордановой лестницы определяет
клетки на главной диагонали матрицы
на главной диагонали матрицы ;
число таких клеток
;
число таких клеток –го
порядка
–го
порядка .
.
3) Рассмотрим все
столбцы жордановой лестницы, тогда
матрица
 в каноническом базисе имеет вид:
в каноническом базисе имеет вид:
 .
.
Число клеток = числу
столбцов в жордановой лестнице =
 - геометрической кратности корня.
- геометрической кратности корня.
 -
алгебраическая кратность корня.
-
алгебраическая кратность корня.
Число клеток
 -того
порядка:
-того
порядка:
 .
.
Процесс построения
канонического базиса однозначно
определяет форму матрицы
 с точностью до порядка клеток, т.к.
количество клеток =
с точностью до порядка клеток, т.к.
количество клеток = ,
а число клеток
,
а число клеток –го
порядка
–го
порядка


Практический способ построения жорданова базиса.
Пусть
 - собственное значение алгебраической
кратности
- собственное значение алгебраической
кратности
1) Найдем
 - максимальную высоту корневого вектора:
- максимальную высоту корневого вектора: .
. – максимальный размер жордановой
клетки, отвечающий данному
– максимальный размер жордановой
клетки, отвечающий данному .
.
2) Найдем начало
цепочки:
 .
.
 ,
восстанавливаем всю цепочку:
,
восстанавливаем всю цепочку:
 (лучше начинать с
(лучше начинать с , т.к.
, т.к. ,
а потом находить остальные:
,
а потом находить остальные: ).
).
3) Переходим к другому
вектору, принадлежащему
 .
Если число в этих цепочках меньше
.
Если число в этих цепочках меньше ,
то переходим к
,
то переходим к .
.