Лекции по ТОЭ6 / Часть 2 / Часть 2 / Перех.проц2
.doc
4.2.6. Переходные процессы в цепях второго порядка
Одна из классических задач в теории переходных процессов – анализ разряда конденсатора на цепь RL.
4.2.6.1. Разряд емкости на цепь RL
1. Независимые начальные условия для рассматриваемой цепи (рис. 4.15):
![]()
2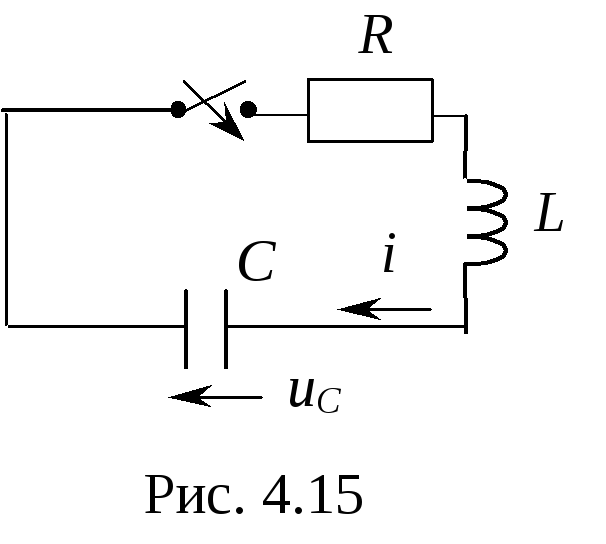 . Дифференциальное
уравнение цепи и корни характеристического
уравнения:
. Дифференциальное
уравнение цепи и корни характеристического
уравнения:
![]()
![]() ;
;
![]() .
.
Характеристическое уравнение
![]() или
или
![]() . (4.11)
. (4.11)
Корни характеристического уравнения
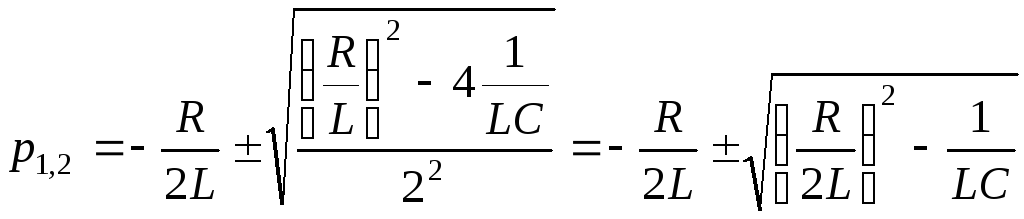 . (4.12)
. (4.12)
3. Полное решение
![]() .
Вид свободной составляющей и характер
переходного процесса будут определяться
тем, какими числами будут корни
характеристического уравнения. Это
зависит от соотношения между параметрами
цепи, в частности, от подкоренного
выражения в уравнении (4.12). Здесь возможны
три варианта:
.
Вид свободной составляющей и характер
переходного процесса будут определяться
тем, какими числами будут корни
характеристического уравнения. Это
зависит от соотношения между параметрами
цепи, в частности, от подкоренного
выражения в уравнении (4.12). Здесь возможны
три варианта:
-
 ,
где – волновое
сопротивление контура, т.е. для
низкодобротных контуров Q
< 0,5. При этом корни p1
и p2
– вещественные
отрицательные разные.
,
где – волновое
сопротивление контура, т.е. для
низкодобротных контуров Q
< 0,5. При этом корни p1
и p2
– вещественные
отрицательные разные. -
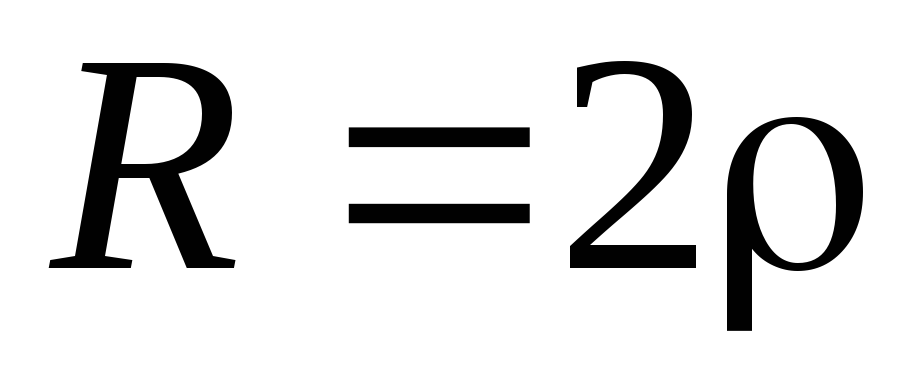 или Q = 0,5:
корни p1 = p2 –
вещественные отрицательные равные
или Q = 0,5:
корни p1 = p2 –
вещественные отрицательные равные -
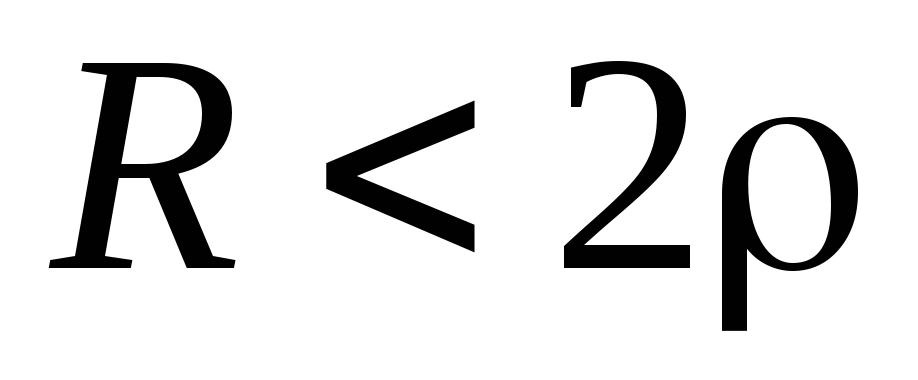 или Q > 0,5: корни p1 и p2
– комплексные сопряженные.
или Q > 0,5: корни p1 и p2
– комплексные сопряженные.
В первых двух случаях переходный процесс носит апериодический характер (напряжение на емкости uC монотонно затухает до нуля, не меняя своей полярности); в третьем случае процесс разряда – колебательный.
4.2.6.2. Апериодический емкости на цепь RL
Рассмотрим
случай, когда p1,2
– действительные
и отрицательные,
т.е.
![]() .
В этом
случае переходный процесс называется
апериодическим
и вид полного решения следующий:
.
В этом
случае переходный процесс называется
апериодическим
и вид полного решения следующий:
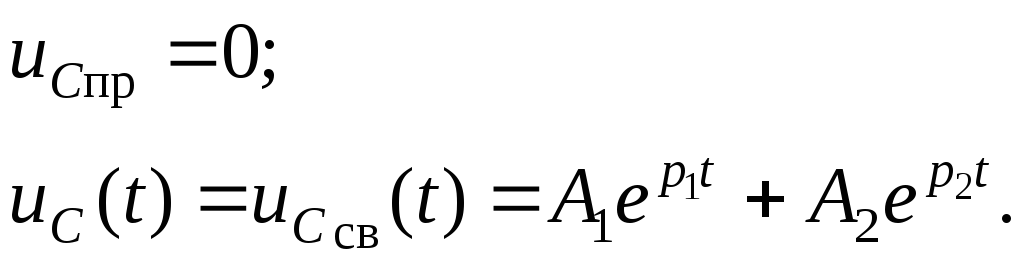
Найдем постоянные интегрирования А1 и А2:
![]() ;
;
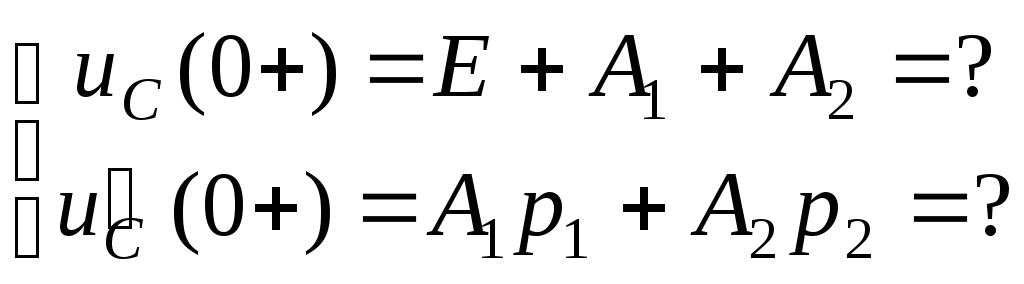
![]()
![]()

![]() ;
аналогично:
;
аналогично:
![]() .
.
Таким
образом, искомое
![]() имеет
вид:
имеет
вид:
![]() .
.
![]() ;
;
![]() .
.
Качественно изобразим график (рис. 4.15).
Рассмотрим начальные значения:
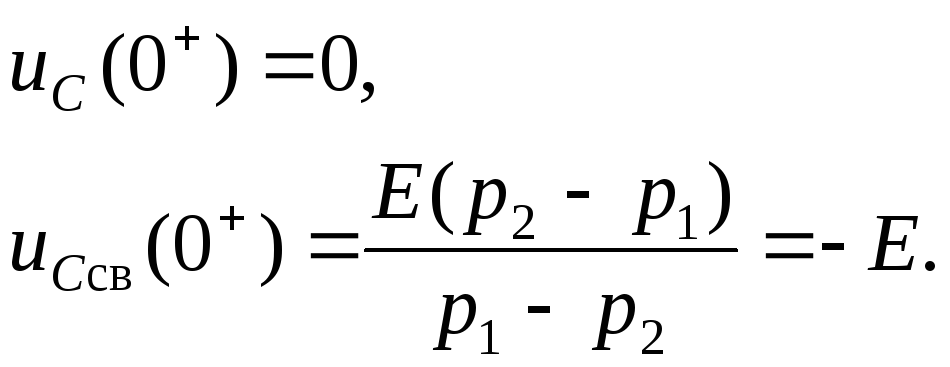
П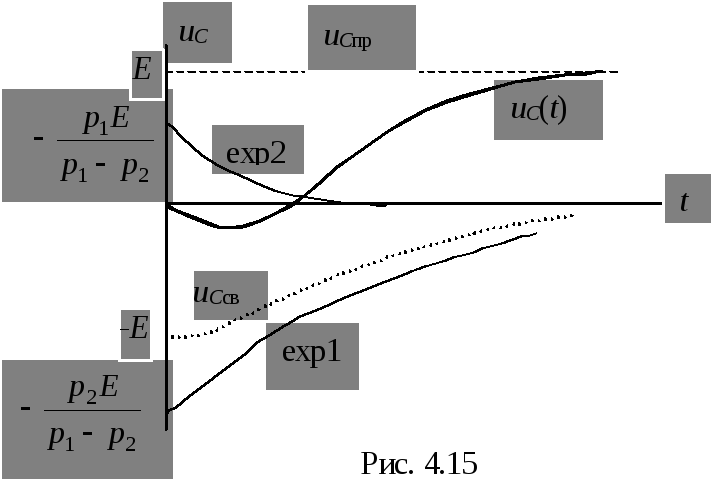 олучим
функцию изменения тока в цепи:
олучим
функцию изменения тока в цепи:
![]() .
.
С учетом того, что по теореме Виета
![]() ,
,
![]() .
.
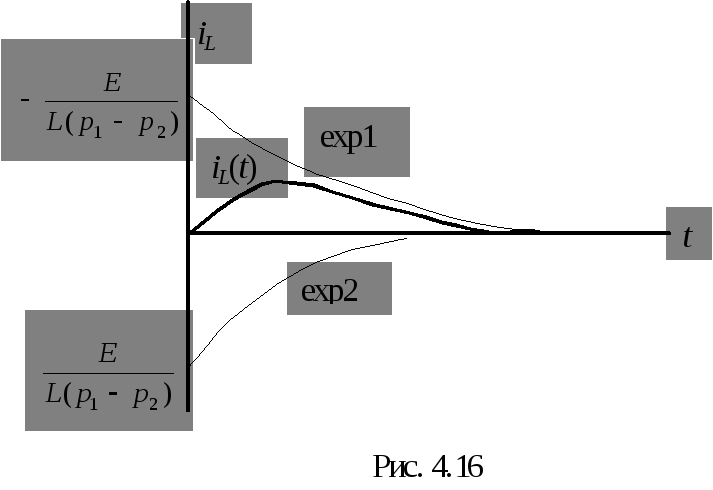
Для
построения графика (рис. 4.16) проведем
аналогичные изложенным выше исследования.
Поскольку
![]() ,
первая экспонента имеет большую
постоянную времени и обращается в нуль
за больший промежуток времени. Так как
,
первая экспонента имеет большую
постоянную времени и обращается в нуль
за больший промежуток времени. Так как
![]() ,
,
![]() ,
,
![]() ,
тогда
,
тогда
![]()
Получим функцию изменения напряжения на индуктивности
![]() .
.
С учетом сказанного выше, exp1 находится в нижней полуплоскости и имеет большую постоянную времени, а exp2 находится в верхней полуплоскости и устремляется к нулю за меньший промежуток времени (рис. 4.17).
Начальные
условия определяются следующим образом
![]() .
Поскольку
.
Поскольку
![]() ,
модули exp1, 2 отличаются
на E, причем exp1(0+) < exp2(0+).
,
модули exp1, 2 отличаются
на E, причем exp1(0+) < exp2(0+).
4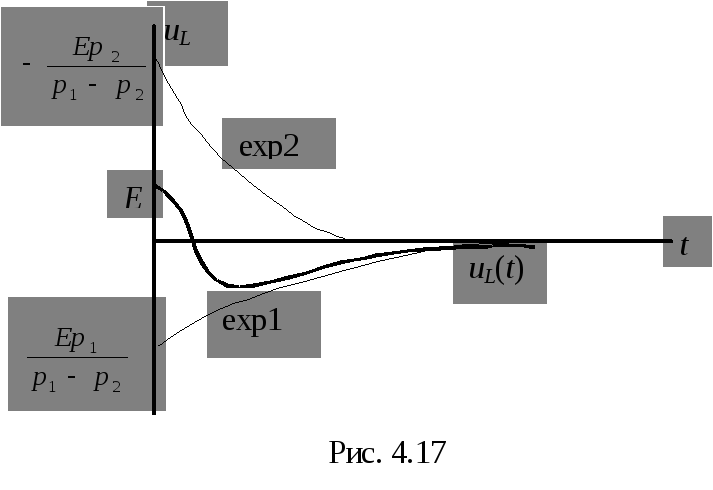 .2.5.3.
Колебательный заряд конденсатора
.2.5.3.
Колебательный заряд конденсатора
В
случае, если корни характеристического
уравнения p1,2
комплексные сопряженные, переходный
процесс имеет колебательный
характер. В
данном случае
![]() и подкоренное выражение отрицательное.
Корни характеристического уравнения
в общем случае записываются в виде
и подкоренное выражение отрицательное.
Корни характеристического уравнения
в общем случае записываются в виде
![]() ,
,
где
![]() –
коэффициент
затухания;
–
коэффициент
затухания;
![]() – частота
свободных (собственных) колебаний
контура.
– частота
свободных (собственных) колебаний
контура.
Между
![]() и
и
![]() существует следующая связь
существует следующая связь
![]() .
.
Поскольку все изложенные выше выкладки применимы и для данного случая, запишем полное решение
![]() .
.
Подставив
в данную формулу выражения для
![]() и
и
![]() ,
получим:
,
получим:
![]()
![]()
![]()
![]()
![]()
![]() .
.
Определим ток в контуре
![]()
![]()
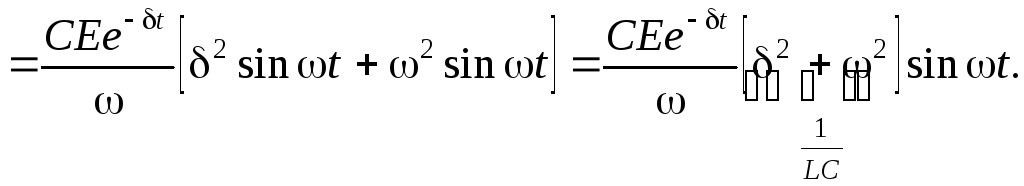
Таким образом,
![]() .
.
Введем
![]() и упростим выражение, полученное для
и упростим выражение, полученное для
![]() :
:
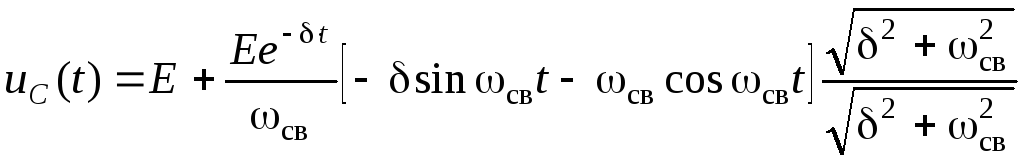 ,
,
тогда,
обозначив
![]() ,
где
,
где
![]() ,
,

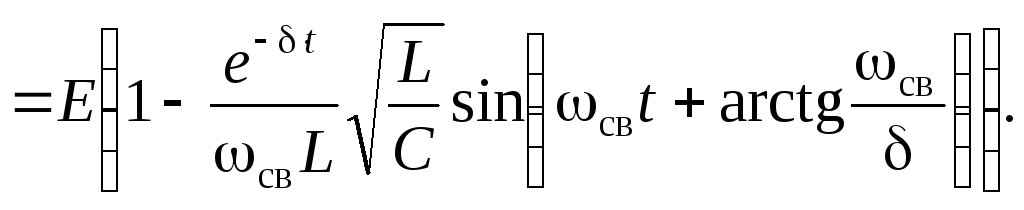
Таким образом,
![]() .
.
При
построении
графиков
следует принимать во внимание соотношение
между постоянной времени экспоненты
![]() и периодом синусоиды
и периодом синусоиды
![]() в свободной составляющей. Рассмотрим
два варианта.
в свободной составляющей. Рассмотрим
два варианта.
1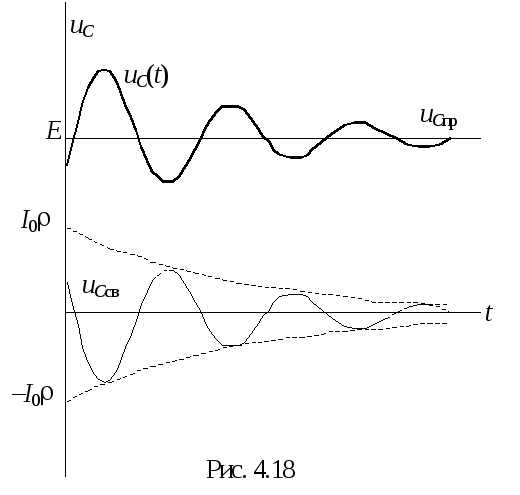 .
. ![]() .
В данном случае возможно графическое
перемножение экспоненты
.
В данном случае возможно графическое
перемножение экспоненты
![]() и синусоиды
и синусоиды
![]() (рис. 4.18).
(рис. 4.18).
2. ![]() .
В данном случае возможно только
аналитическое определение свободной
составляющей (рис. 4.19). Для этого
необходимо оценить время переходного
процесса
.
В данном случае возможно только
аналитическое определение свободной
составляющей (рис. 4.19). Для этого
необходимо оценить время переходного
процесса
![]() ,
где
,
где
![]() .
Далее в зависимости от необходимой
точности построения графика этот
промежуток времени следует разбить на
n
интервалов t
и далее
рассчитать значение искомой функции в
каждый момент
.
Далее в зависимости от необходимой
точности построения графика этот
промежуток времени следует разбить на
n
интервалов t
и далее
рассчитать значение искомой функции в
каждый момент
![]() .
.
П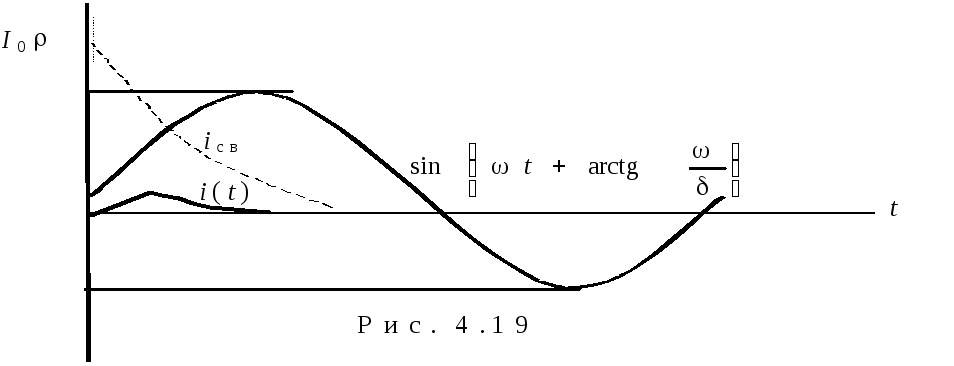 олучим
общий вид системы уравнений для
определения постоянных интегрирования
для случая комплексных корней
характеристического уравнения. Как уже
было показано, полное решение запишется
олучим
общий вид системы уравнений для
определения постоянных интегрирования
для случая комплексных корней
характеристического уравнения. Как уже
было показано, полное решение запишется
![]() .
.
Для определения В1 и В2 составим систему уравнений:
![]()
![]()
![]()
Запишем
![]() для t
= 0+
для t
= 0+
![]()
![]()
Таким образом, искомая система уравнений имеет вид:
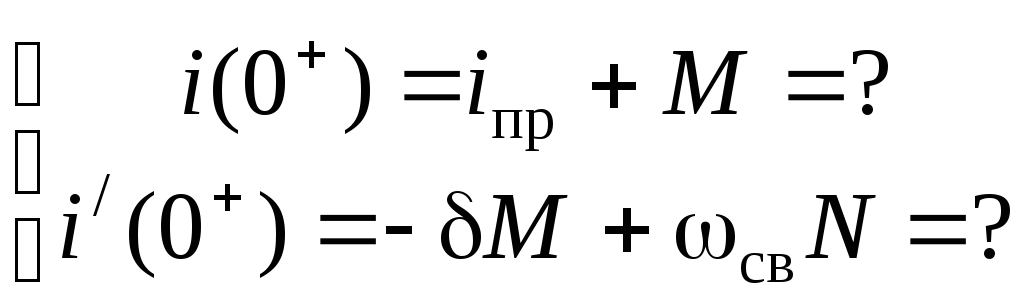
4.2.5.4. Общий случай расчета цепи II порядка
П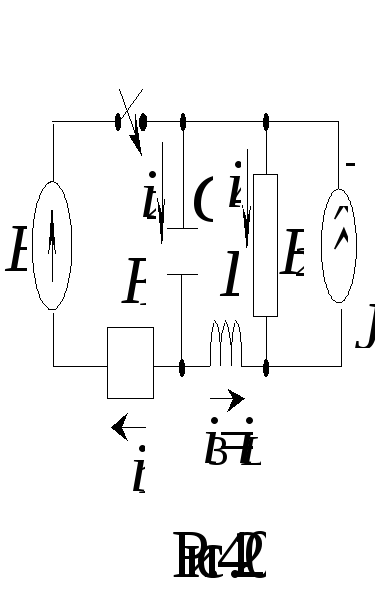 роиллюстрируем
рассмотренную выше методику на примере
цепи второго порядка.
роиллюстрируем
рассмотренную выше методику на примере
цепи второго порядка.
Пусть дана цепь (рис. 4.20) с параметрами Е = 30 В, J = 2 А, R1 = 20 Ом, R2 = 10 Ом, С = 100 мкФ, L = 50 мГн.
Требуется определить закон изменения тока i1(t) после коммутации.
1. Правила коммутации:
iL(0-) = iL(0+) = 0 А,
uC (0-) = uC (0+) = JR2 = 20 B.
2. Составление характеристического уравнения цепи. С помощью совместного решения однородной системы дифференциальных уравнений. Составляем систему дифференциальных уравнений для мгновенных значений токов и напряжений по законам Кирхгофа:
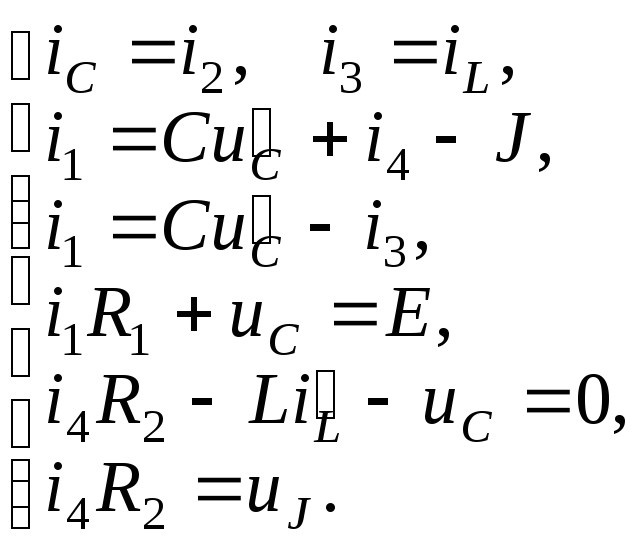
Методом исключения получаем из данной системы дифференциальное неоднородное уравнение
![]()
Соответствующее ему характеристическое уравнение имеет вид
![]()
Подставим значения параметров цепи:
p2 + 700p + 300000 = 0.
Корни характеристического уравнения
p1 = – 350 + j421,308, p2 = – 350 – j421,308
являются комплексными сопряженными, следовательно, переходный процесс в цепи имеет колебательный характер.
3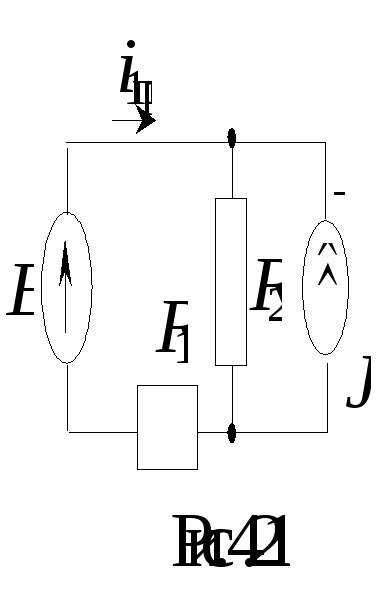 . Определение
принужденной составляющей. Рассматриваемая
цепь в принужденном режиме имеет вид
(рис. 4.21)
. Определение
принужденной составляющей. Рассматриваемая
цепь в принужденном режиме имеет вид
(рис. 4.21)
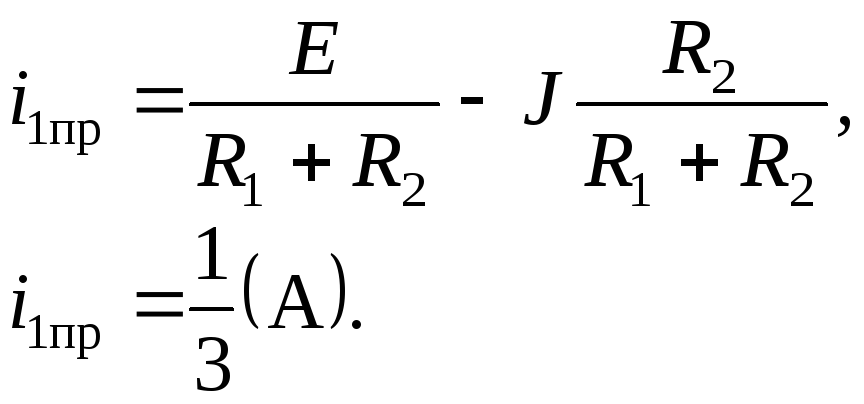
4. Определение свободной составляющей. Для цепей, характеристические числа которых имеют комплексные сопряженные значения, свободная составляющая определяется в виде
![]() ,
,
где – декремент затухания,
– частота
свободных колебаний определяются через
корни характеристического уравнения
![]() .
.
Таким образом, в выражении i1св необходимо определить постоянные интегрирования А1 и А2. Вычисление их ведется с помощью системы уравнений, составленных для момента t = 0+:
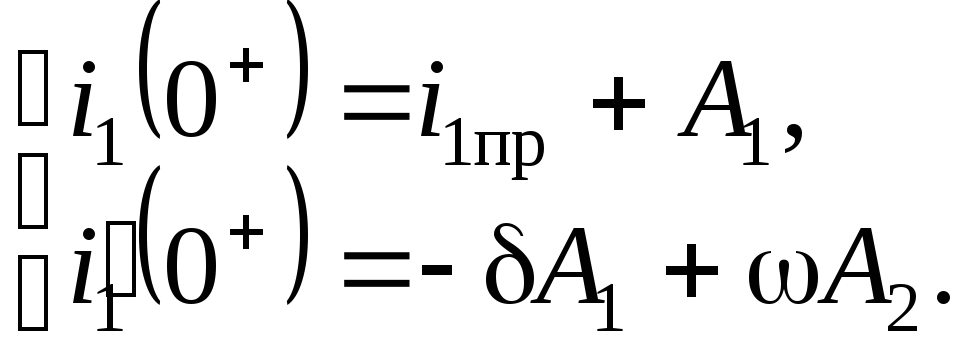
4.1.
Определение значений
![]() и
и
![]() с использованием системы уравнений
Кирхгофа. В данном случае составляется
система уравнений Кирхгофа. Методом
исключения выражается значение тока
с использованием системы уравнений
Кирхгофа. В данном случае составляется
система уравнений Кирхгофа. Методом
исключения выражается значение тока
![]() через известные значения uC(0+)
и i2(0+):
через известные значения uC(0+)
и i2(0+):
![]() .
.
Дифференцируя выражение для i1(t), получим
![]() .
.
Произведя необходимые преобразования и подстановки в системе уравнений Кирхгофа, получим
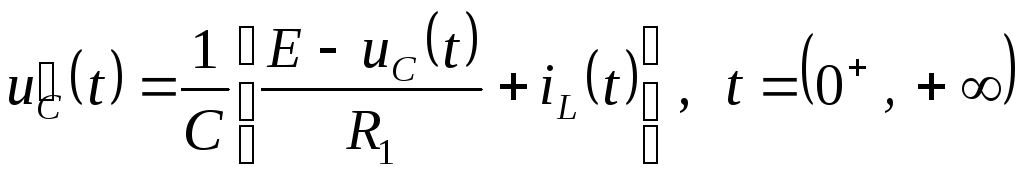 .
.
Подставив соответствующие значения uC и iL в момент t = 0+, рассчитаем
![]() A/с.
A/с.
4.2.
Определение i1(0+)
и
![]() с использованием
резистивных схем замещения
в момент t = 0+.
При построении схемы замещения в 0+:
с использованием
резистивных схем замещения
в момент t = 0+.
При построении схемы замещения в 0+:
–источники с ЭДС или задающим током, номиналы резисторов оставить неизменными;
– емкости
и индуктивности же заменить в соответствии
со следующим правилом: емкости с нулевыми
начальными условиями (![]() )
заменяются короткозамкнутыми участками,
с ненулевыми начальными условиями (
)
заменяются короткозамкнутыми участками,
с ненулевыми начальными условиями (![]() )
заменяются противодействующими
источниками ЭДС с
)
заменяются противодействующими
источниками ЭДС с
![]() ;
;
– ветви
с индуктивностями, имеющими нулевые
начальные условия (![]() ),
размыкаются, в случае ненулевых начальных
условий (
),
размыкаются, в случае ненулевых начальных
условий (![]() )
индуктивности заменяют на содействующие
источники тока с
)
индуктивности заменяют на содействующие
источники тока с
![]() .
.
Схема замещения в 0+ для величин токов и напряжений изображена на рис. 4.22.
![]()
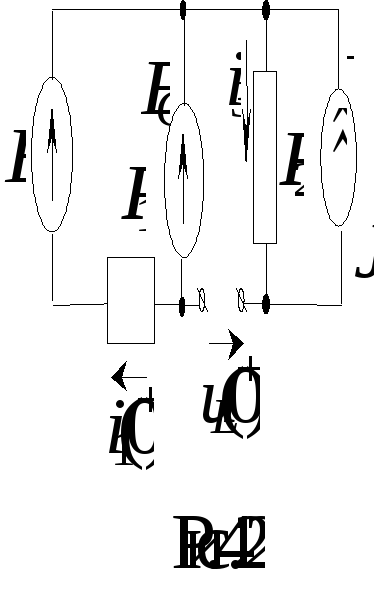
По II закону Кирхгофа получим
![]() .
.
Для построения схемы замещения в (0+) для производных токов и напряжений необходимо определить начальные значения:
![]()
Таким образом, следует определить iC(0+) и uL(0+) с помощью уже полученной схемы замещения:
а) для определения uL(0+) составим уравнение по II закону Кирхгофа:
![]() ,
,
подставив
значения, получим uL(0+)
= 0, следовательно,
![]() .
.
б)
iC(0+)
= i1(0+)
= 0,5 A, следовательно,
![]() = 5000 B/с.
= 5000 B/с.
При построении схемы замещения в 0+ для производных следует:
– источники заменить на аналогичные источники с ЭДС или задающим током, равным соответственно производной от данных в задании;
– номиналы резисторов оставить неизменными;
– емкости
и индуктивности же заменить в соответствии
со следующим правилом: емкости с нулевыми
начальными условиями (![]() )
заменяются короткозамкнутыми участками,
с ненулевыми начальными условиями (
)
заменяются короткозамкнутыми участками,
с ненулевыми начальными условиями (![]() )
заменяются противодействующими
источниками ЭДС с
)
заменяются противодействующими
источниками ЭДС с
![]() ;
;
– ветви
с индуктивностями, имеющими нулевые
начальные условия (![]() ),
размыкаются, в случае ненулевых начальных
условий (
),
размыкаются, в случае ненулевых начальных
условий (![]() )
индуктивности заменяют на содействующие
источники тока с
)
индуктивности заменяют на содействующие
источники тока с
![]() .
.
Таким образом, осуществляется операция дифференцирования, адекватная дифференцированию системы уравнений Кирхгофа.
В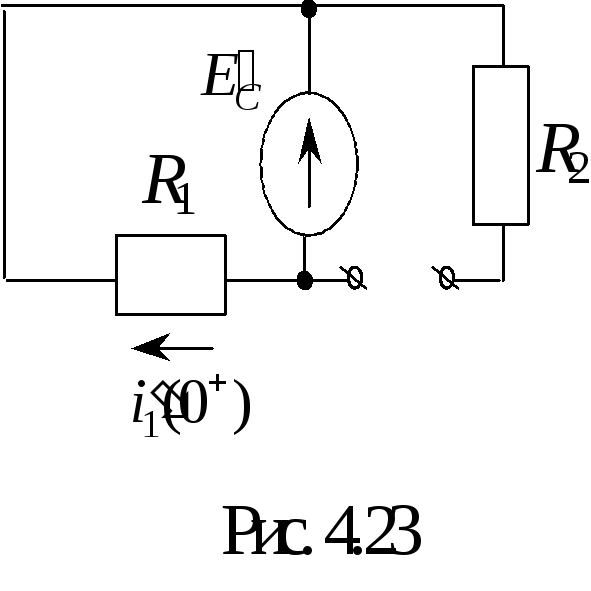 нашем случае, когда в цепи действуют
источники постоянных воздействий,
источники ЭДС заменяются короткозамкнутыми
участками (т.к.
нашем случае, когда в цепи действуют
источники постоянных воздействий,
источники ЭДС заменяются короткозамкнутыми
участками (т.к.
![]() ),
а ветви с источниками тока размыкаются
(т.к.
),
а ветви с источниками тока размыкаются
(т.к.
![]() ).
).
Таким
образом, схема замещения в t
= 0+
для производных имеет вид (рис. 4.23).
Определим
![]() .
.
4.3. Определение постоянных интегрирования:
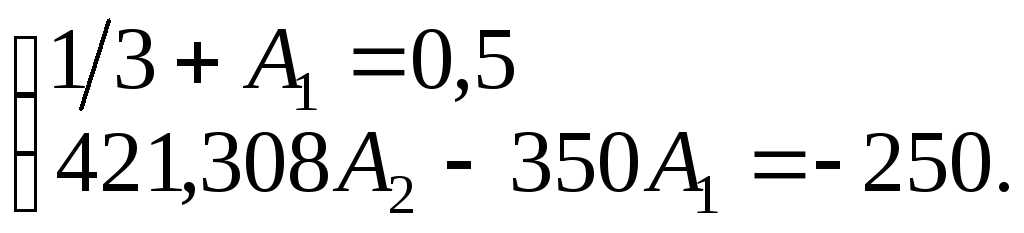
Решив данную систему уравнений, получим
А1 = 0,1667, А2 = – 0,455.
5. Определение полного решения. Полное решение следует искать в виде
i1(t) = i1пр + i1св.
С учетом произведенных расчетов получим
![]()
Для удобства преобразуем полученное выражение в синусоидальную форму:
![]() .
.
Таким образом, искомый ток изменяется по следующему закону
i1(t) = 1/3 + 0,485e-350t sin(421,308t + 2,788).
График изменения i1(t) представлен на рис. 4.24.

Порядок расчета переходных процессов классическим методом:
-
расчет принужденной составляющей
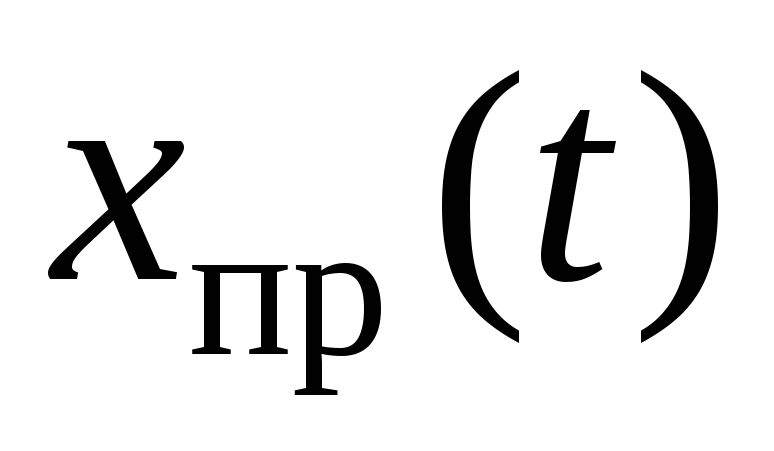 переходного процесса;
переходного процесса; -
определение корней характеристического уравнения;
-
определение свободной составляющей
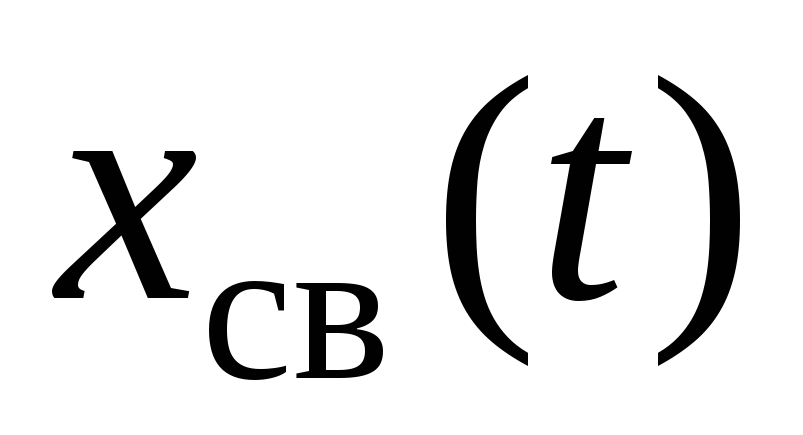 переходного процесса в зависимости от
полученных корней;
переходного процесса в зависимости от
полученных корней; -
запись полного решения
 ;
; -
определение независимых начальных условий (ток в индуктивности и напряжение на конденсаторе) из расчета докоммутационного режима;
-
определение постоянных интегрирования;
-
нахождение окончательного решения
 .
.
Классический метод анализа переходных процессов, будучи прозрачным и наглядным, имеет недостатки, связанные с громоздкой процедурой определения начальных условий, которые усугубляются с ростом порядка исследуемой цепи.