Экзамен / тмм - экзамен(и задачи) / ТММ Экзамен! / Лекции / шпоры динамика / 15

6.2. Уравнения Лагранжа второго рода

для механизма с несколькими степенями подвижности

Уравнения Лагранжа второго рода для механизма с w степенями подвижности, с жесткими звеньями и идеальными кинематическими парами могут быть получены из общего уравнения динамики, записанного в форме (4.28). Работа сил инерции на возможном перемещении, входящая в это уравнение, может быть выражена через кинетическую энергию системы. Для механизма с w степенями подвижности справедливо:

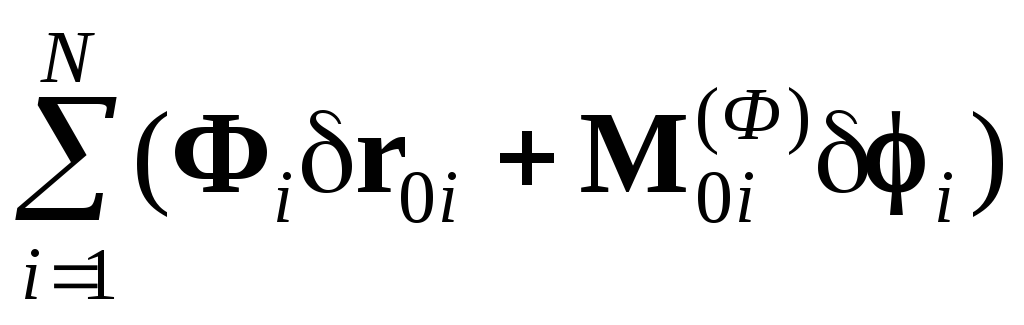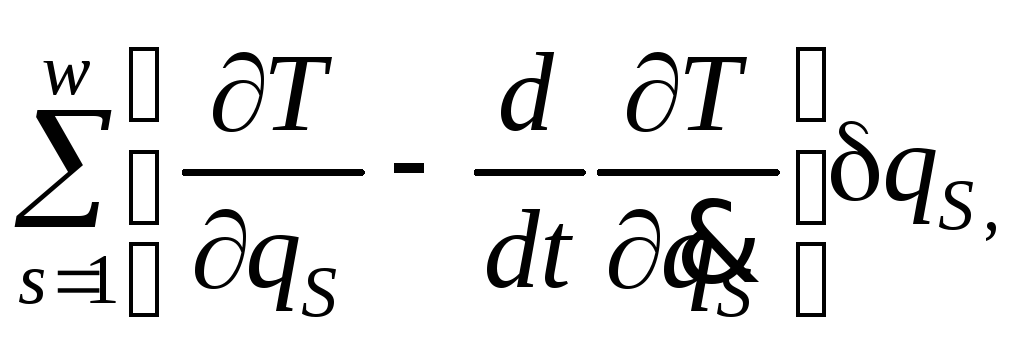= (6.17)

где Т(q₁, …, q_w,) – кинетическая энергия механизма с w степенями подвижности, представленная как функция от обобщенных координат и их производных. В результате при независимых обобщенных координатах уравнения (4.34) приводятся к виду:

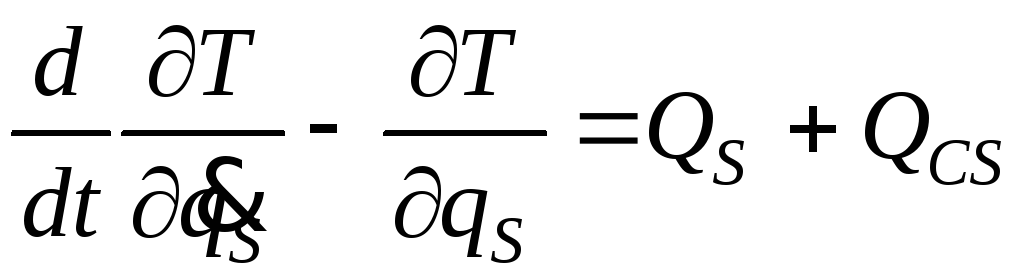(s = 1, … , w) , (6.18)

где Q_S – обобщенные движущие силы;

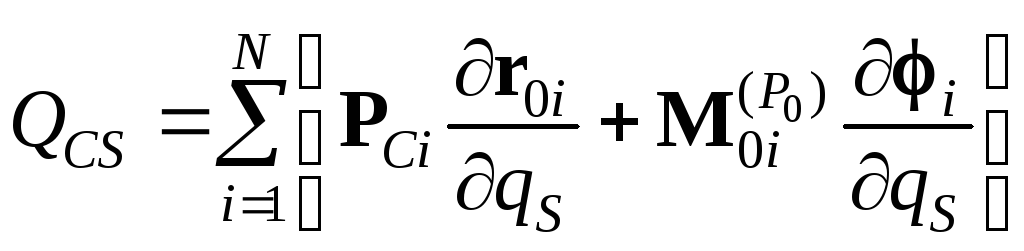(6.19)

– обобщенные силы сопротивления, соответствующие всем активным силам, кроме движущих.

Кинетическая энергия каждого звена в общем случае определяется как кинетическая энергия твердого тела, совершающего сложное пространственное движение:

, (6.20)

где i – номер звена, m_i – его масса, v_ci – скорость центра масс, J_iС – тензор инерции в системе осей, начало которой находится в центре масс i-го звена, – трехмерный вектор-столбец абсолютной угловой скорости. Учитывая, что

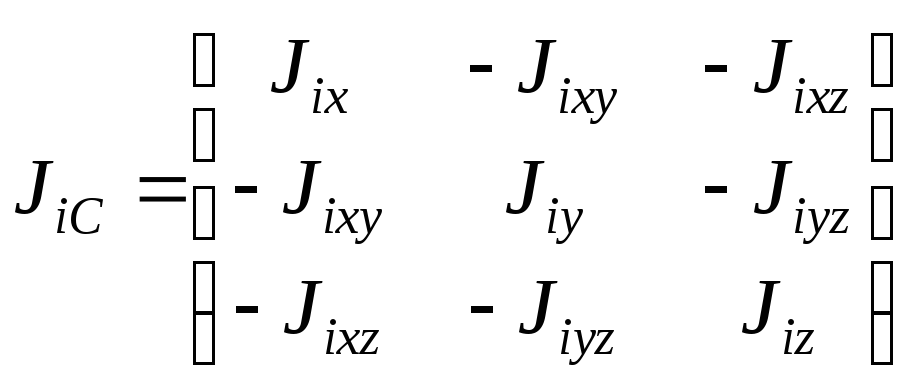, (6.21)

где J_ix, J_iy, J_iz – осевые моменты инерции i-го звена, J_ixy, J_ixz, J_iyz – центробежные моменты инерции, а

, (6.22)

где – проекции вектора угловой скорости i-го звена на оси i-й системы координат, выражение (6.20) можно записать в виде:

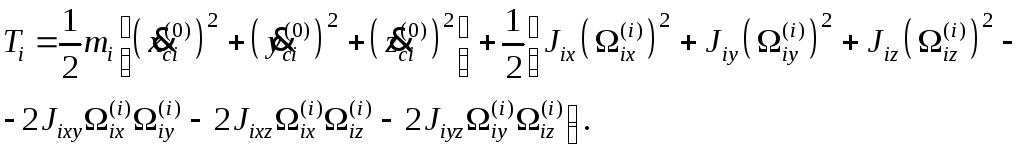(6.23)

В качестве примера рассмотрим схему трехподвижного механизма (рис.6.3). Звено 1 вращается вокруг своей продольной оси с угловой скоростью . По звену 1 со скоростью движется звено 2. Звено 3, связанное со звеном 2 шарниром В, вращается относительно звена 2 с угловой скоростью . На звене 3 имеется схват, в точке М которого приложена активная сила . Центры масс второго и третьего звеньев находятся в точках С₂ и С₃ соответственно.

Кинетическую энергию механизма определим как сумму кинетических энергий его подвижных звеньев. Для вращающегося звена 1 имеем где – момент инерции звена 1 относительно оси z₁, совпадающей с осью его вращения.

Звено 2 вращается вместе со звеном 1 и перемещается по нему, его кинетическая энергия равна:

,

где v_C2 – скорость центра масс второго звена, m₂ – его масса, J₂ – тензор инерции, построенный в осях С₂x₂y₂z₂ (рис.6.4, а), – вектор-столбец угловой скорости.

Найдем v_C2 и :

,

.

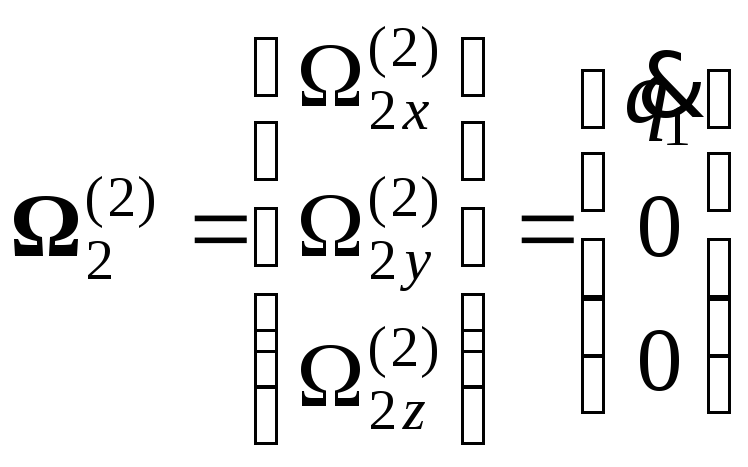Подставим найденные значения в выражение для кинетической энергии Т₂:

,

где . Кинетическая энергия третьего звена Т₃:

.

Найдем скорость центра масс третьего звена v_C3.

,

,

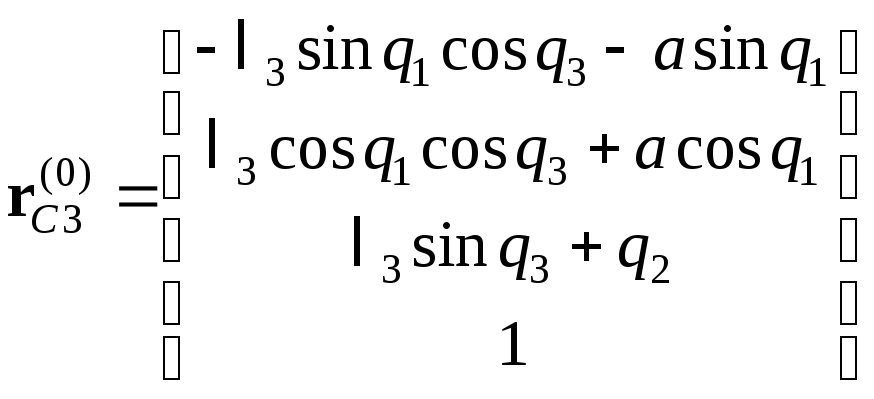Положим, что звено 3 представляет собой тонкий однородный стержень, а . Тогда компоненты тензора инерции J₃, построенного в осях С₃x₃y₃z₃ (рис. 6.4, б): J_3x = 0; J_3y = J_3z = ; J_3xy = J_3xz = J_3yz = 0. Угловая скорость :

.

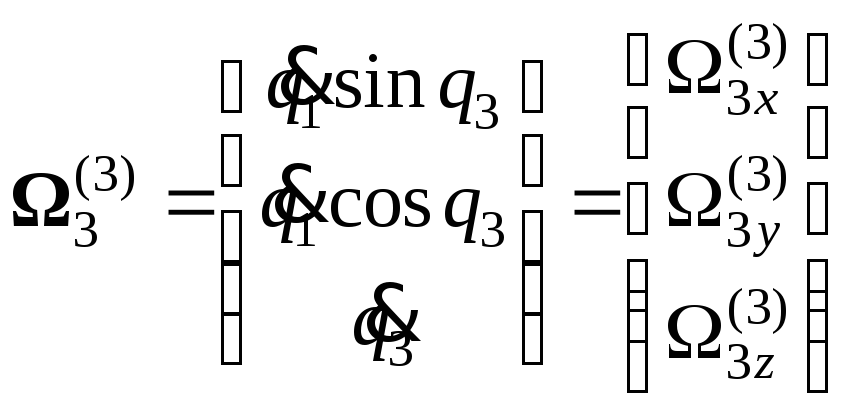Отсюда получим:

.

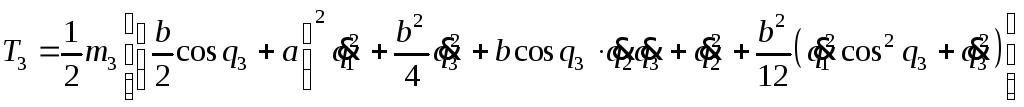Полная кинетическая энергия механизма составит:

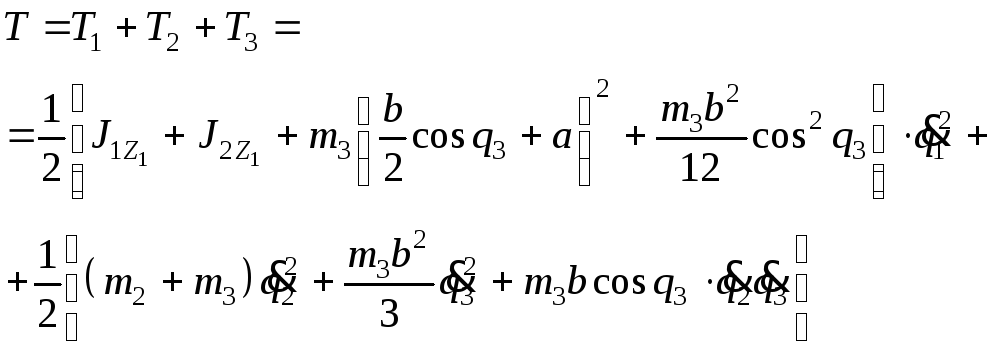
Найдем обобщенные силы сопротивления. Из выражения (6.19) следует:

.

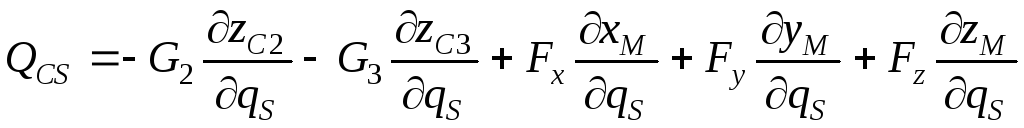Здесь учтено, что центр масс звена 1 не изменяет своего положения. Из кинематического анализа несложно получить выражения для и : , , , , , .

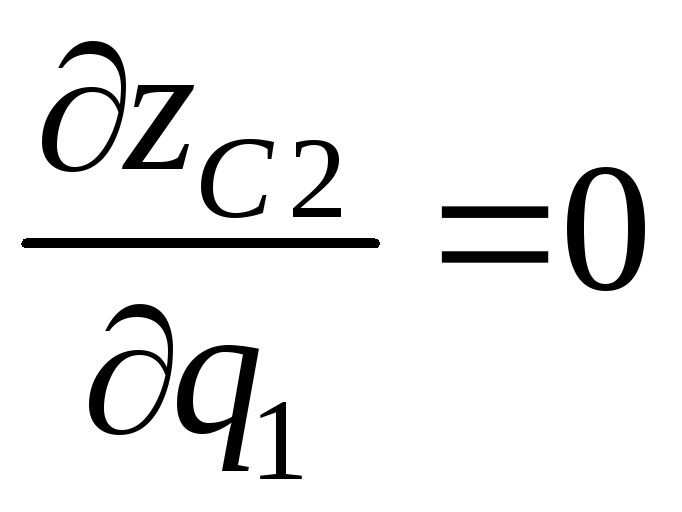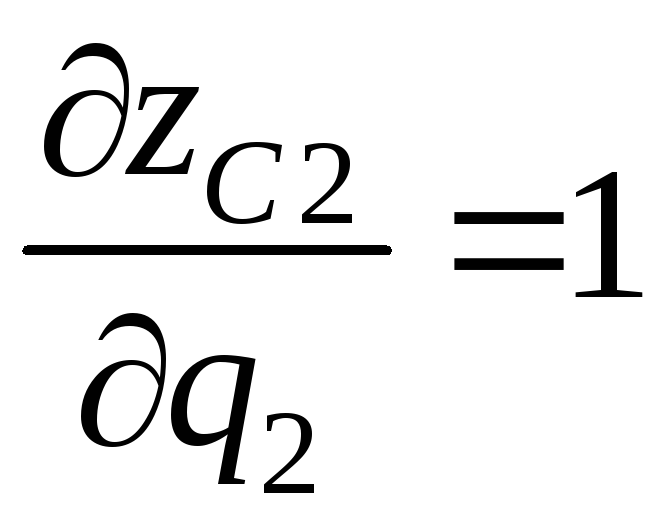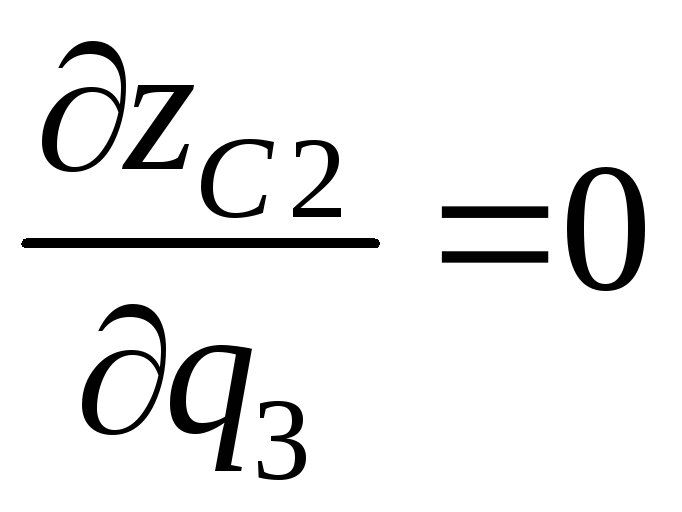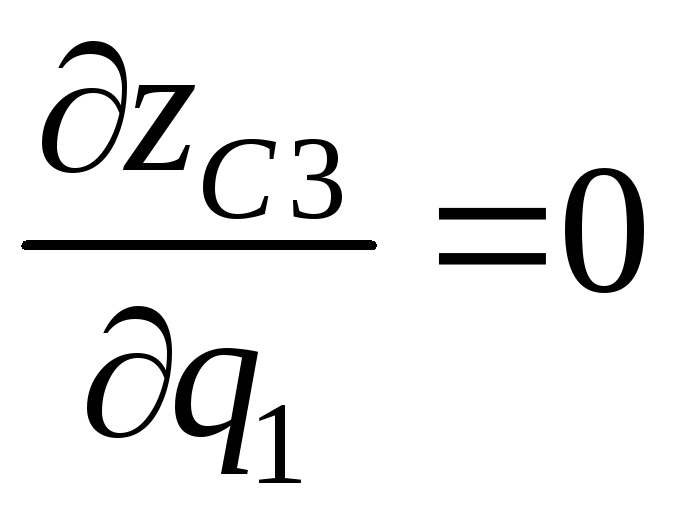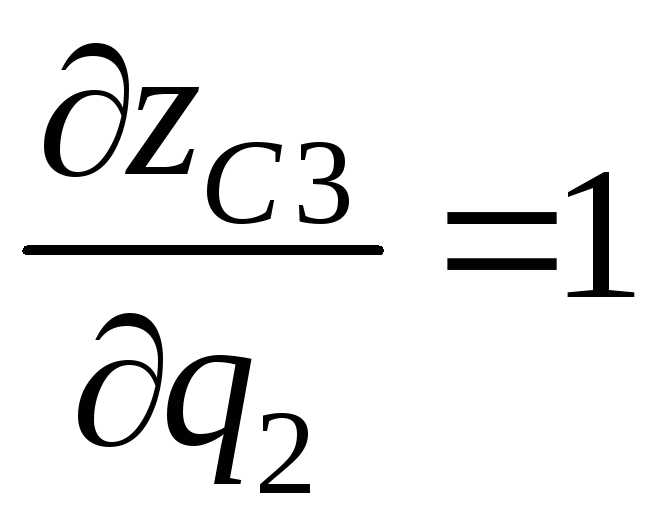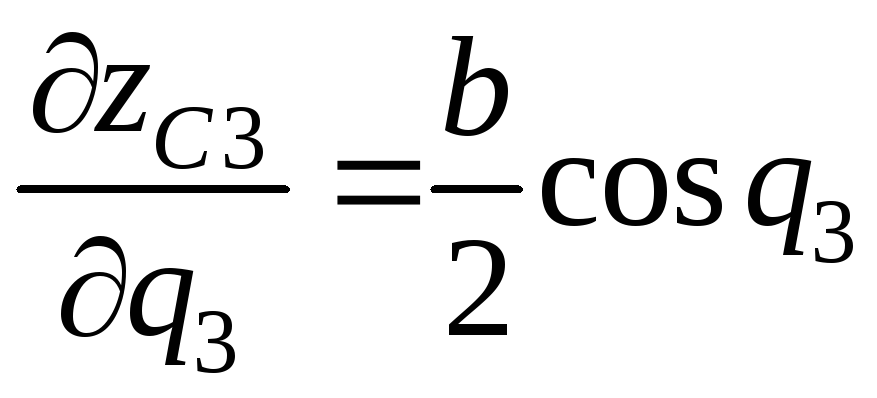Функция положения точки М:

.

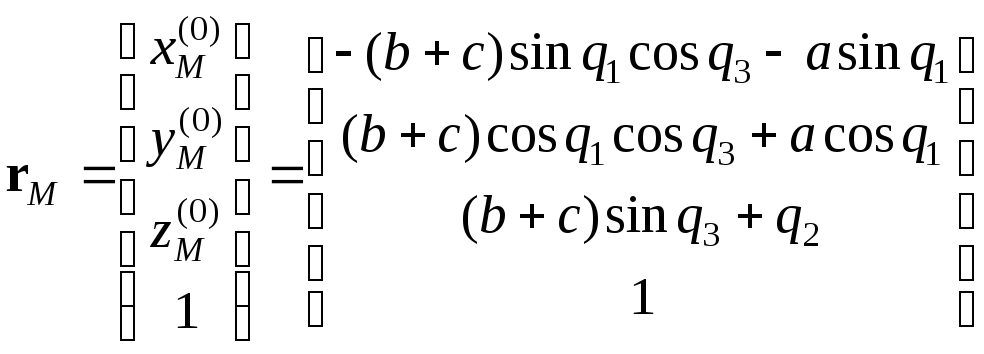Отсюда

, , ,

; ; ,

, , .

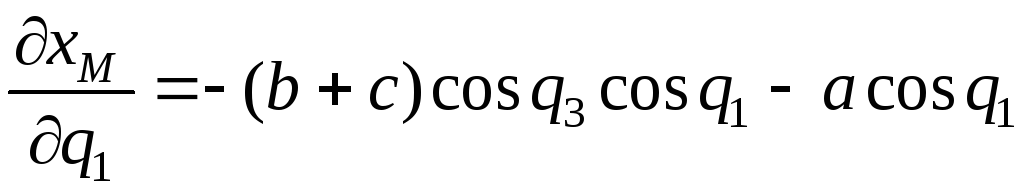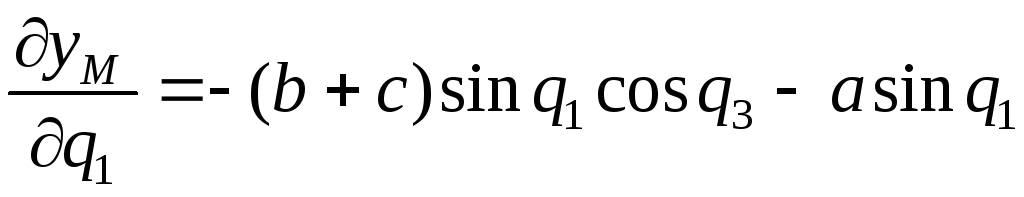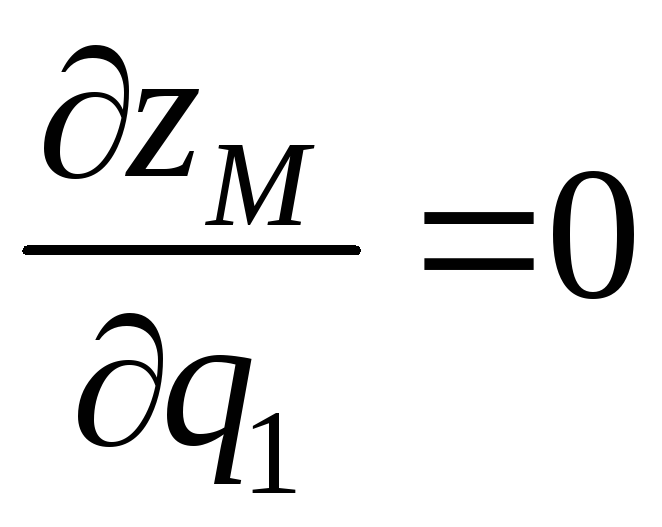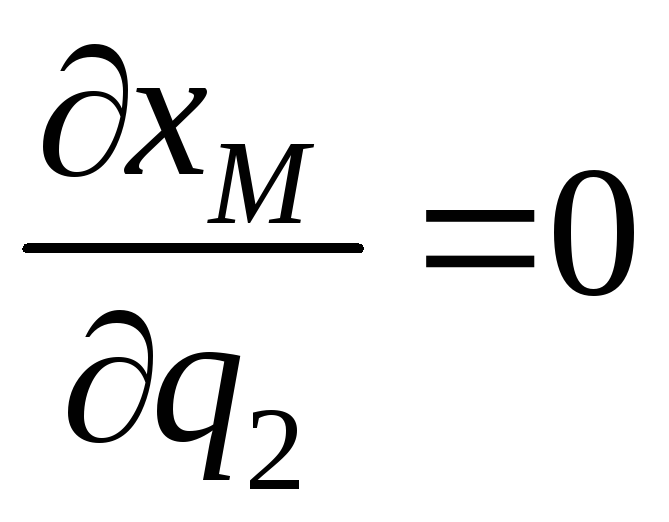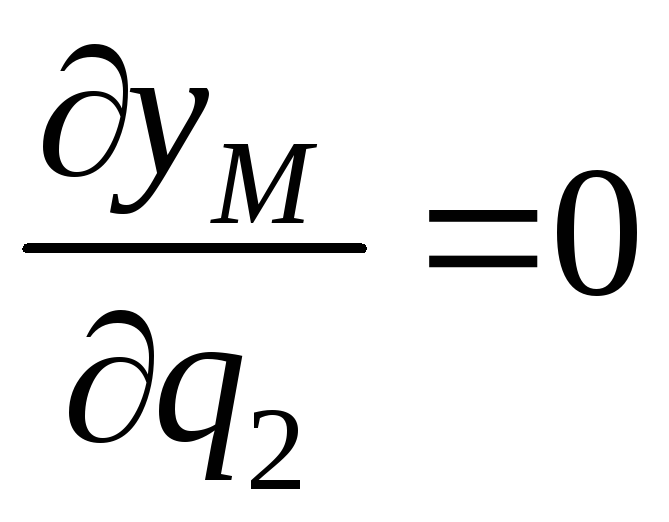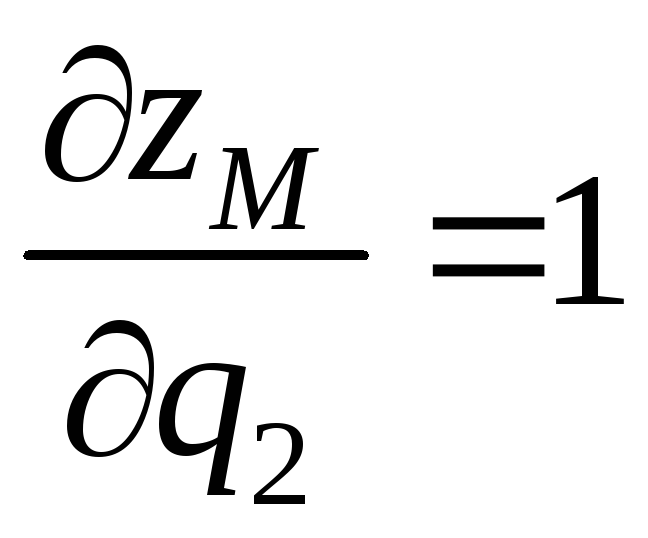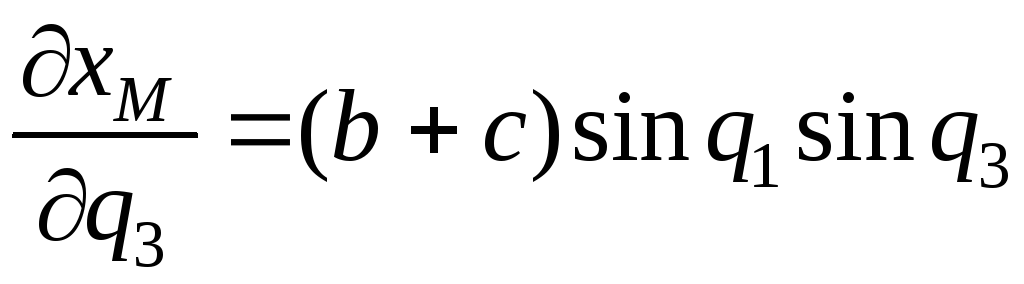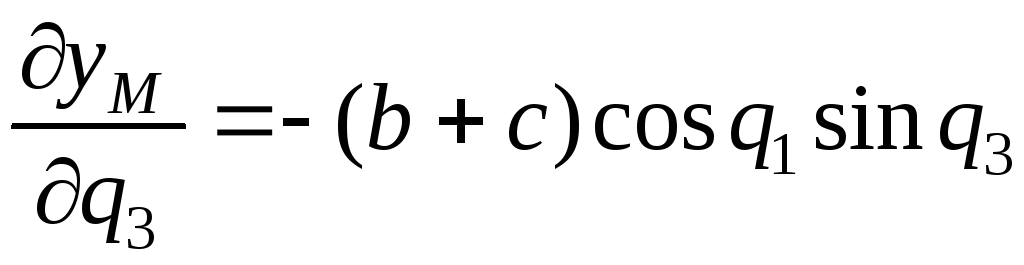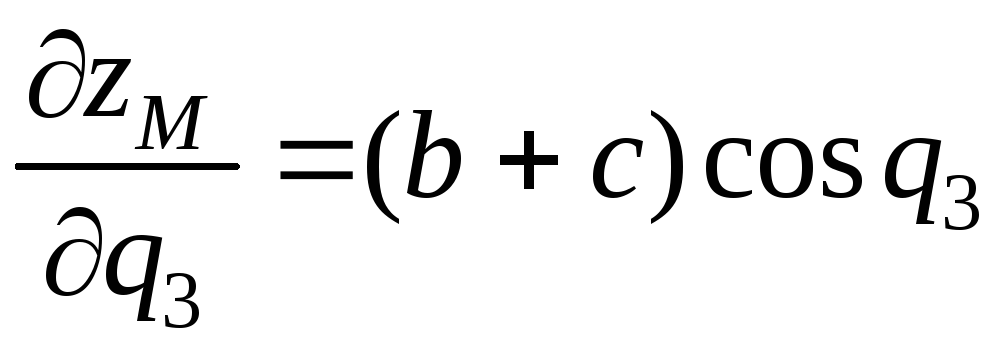Теперь несложно найти обобщенные силы сопротивления:

,

,

.

Подставляя найденные значения в уравнения Лагранжа, получим три уравнения движения:

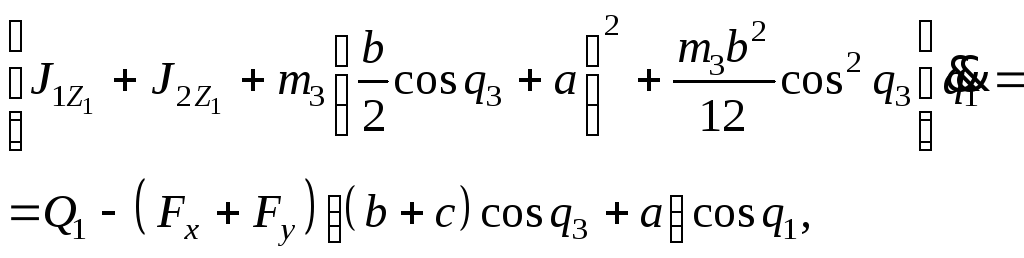
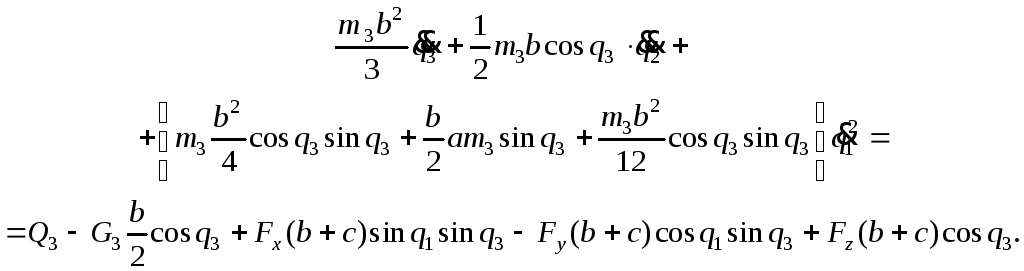
Из приведенных уравнений видно взаимовлияние приводов. Например, двигатель 2 «чувствует», как работает двигатель, приводящий в движение звено 3 (движущий момент Q₂ зависит от и от ).

167