Экзамен / тмм - экзамен(и задачи) / ТММ Экзамен! / Лекции / часть2 / tmm_10

Глава 4. силовой расчет механизмов

4.1. Постановка задачи силового расчета

В курсе теоретической механики рассматривались две задачи динамики:

1. Дан закон движения материальной точки известной массы; требуется найти силу, действующую на точку (первая задача динамики);

2. Дана сила, приложенная к материальной точке; требуется найти закон движения точки (вторая задача динамики).

В теории механизмов и машин также ставятся и решаются две задачи динамики. В частности, первая задача динамики: при известном (заданном) законе движения ведущего звена (ведущих звеньев) механизма требуется найти силы, действующие в механизме. Решение этой задачи называют силовым расчетом. Он имеет большое значение при проектировании машин и механизмов, особенно таких, которые передают большие усилия, т.к. найденные силы используются для дальнейших расчетов на прочность, жесткость и т.д., а также для выбора двигателя (двигателей).

Обычно при силовом расчете предполагается, что ведущее звено (звенья) совершают программное движение, необходимое для выполнения рабочего процесса. В дальнейшем законы движения могут уточняться в соответствии с результатами динамического анализа (решения второй задачи динамики), который будет рассматриваться далее.

При силовом расчете механизма считаются известными все активные силы, действующие на звенья механизма, кроме обобщенных движущих сил. К заданным активным силам относятся:

а) Рабочая нагрузка P – сила, действующая на рабочее звено при выполнении рабочего процесса. Например, сила резания в металлорежущем станке, силы сопротивления грунта, действующие на ковш экскаватора, силы давления воздуха на поршень компрессора и т.п. В некоторых случаях рабочая нагрузка представляет собой момент, например, момент электромагнитных сил, возникающих при вращении ротора электрического генератора, момент сил аэродинамического сопротивления, возникающих в роторных насосах, и т.д.

Рабочая нагрузка обычно не является постоянной. Часто она изменяется по мере перемещения рабочего звена. В этом случае может быть построена зависимость Р = Р(х), где Р – рабочая нагрузка, х – координата точки приложения нагрузки. В более сложных случаях нагрузка зависит также от скорости , ускорения и времени t: . Эти зависимости изучаются в специальных дисциплинах. При выполнении силового расчета они считаются заданными, но их следует привести к более удобному виду. Учитывая, что , , 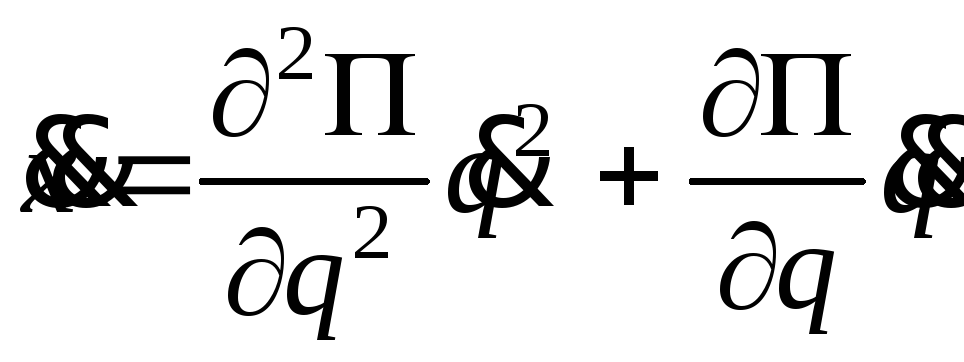можно получить зависимость рабочей нагрузки от обобщенной координаты и ее производных:

. (4.1)

Если в механизме приложена не одна, а рабочих нагрузок, то для них задаются зависимостей:

, (m = 1, 2, … , ) . (4.2)

В многоподвижных механизмах координаты, скорости и ускорения точек приложения нагрузок зависят от всех обобщенных координат и их производных:

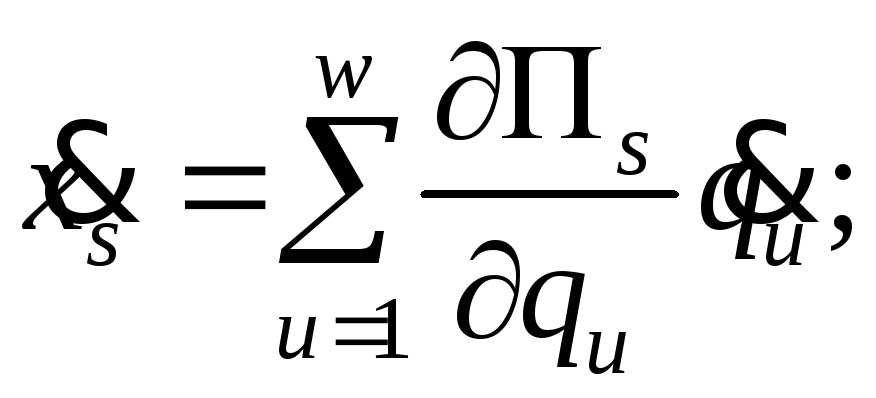
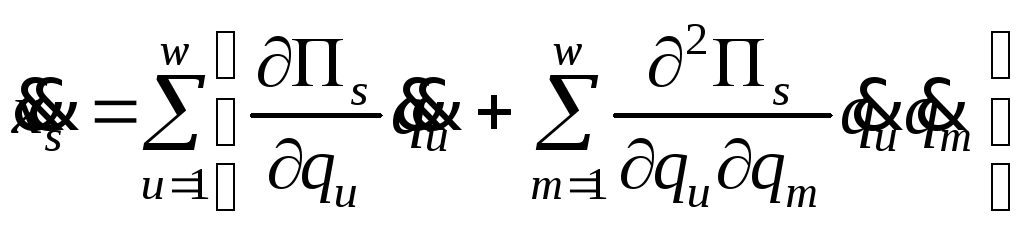, (4.3)

где – функции положения.

Зная (4.3), можно получить зависимости рабочих нагрузок от обобщенных координат и их производных:

, (m = 1, … , ) . (4.4)

В дальнейшем будем предполагать, что рабочие нагрузки не зависят явно от времени и ускорений , поэтому выражения (4.4) будут представляться в форме:

, (m = 1, … , ) (4.5)

б) Cилы тяжести звеньев G_i, , где N – число звеньев. Эти силы являются постоянными, но точки их приложения, а, следовательно, и моменты сил тяжести относительно некоторых центров приведения изменяются в процессе движения.

в) В некоторых механизмах используются пружины, обеспечивающие силовое замыкание кинетических пар (например, в кулачковых механизмах используются пружины, прижимающие толкатель к кулачку). Упругие силы, возникающие при деформации пружин, также являются активными. Их значение зависит от деформации пружин, т.е. от координат точек крепления концов пружины. При заданных законах движения эти силы могут быть определены в любой момент времени или в любом положении механизма.

Целью силового расчета является определение обобщенных движущих сил и реакций во всех кинематических парах. Обобщенные движущие силы – это обобщенные силы, которые необходимо приложить к входным звеньям механизма для того, чтобы получить заданное программное движение при выполнении рабочего процесса. Определив движущие силы, можно выбрать двигатели, приводящие в движение машину.

Реакции в кинематических парах – пассивные силы; как правило, это силы, распределенные по поверхностям соприкосновения конструктивных элементов, образующих пару. Однако в рамках физических моделей кинематических пар, рассматриваемых в курсе теории механизмов и машин, вообще говоря, невозможно определить законы распределения реакций по поверхностям элементов. Поэтому мы ограничимся определением главных векторов и главных моментов сил реакций в каждой кинематической паре.

Рассмотрим вращательную кинематическую пару (рис.4.1); главный вектор сил реакций и главный момент определяются заданием шести скалярных величин – их проекций на оси системы 0xyz.

Определим общее число неизвестных, подлежащих определению при силовом расчете. Пусть механизм имеет w число степеней подвижности и p кинематических пар. Тогда число неизвестных обобщенных движущих сил равно w, а число неизвестных компонент реакций – 6p. Таким образом, общее число неизвестных

n_u = w + 6p = w + 6p₁ + 6p₂ + 6p₃ + 6p₄ + 6p₅ . (4.6)

Эти неизвестные могут быть определены решением уравнений движения звеньев механизма. Пусть число звеньев равно N. Для каждого подвижного звена можно составить два векторных уравнения движения на основе теорем об изменении количества движения и кинетического момента. Если – вектор количества движения s–го звена, а – его кинетический момент, то уравнения движения записываются в виде:

(4.7)

где – внешние силы, действующие на s–е звено, – радиусы-векторы точек их приложения, g_s – число сил, приложенных к s–му звену. Как известно из курса теоретической механики, другие независимые уравнения движения для твердого тела составить невозможно. Общее число векторных уравнений (4.7) равно 2(N–1); проецируя их на оси координат, получаем 6(N–1) скалярных уравнений.

Пусть механизм не содержит избыточных связей. Тогда для него справедлива формула

(4.8)

где p_s– число s–подвижных пар. Из уравнения (4.8) можно выразить число уравнений n_eq = 6(N–1):

.

Сравнивая число неизвестных n_u и число уравнений n_eq , имеем:

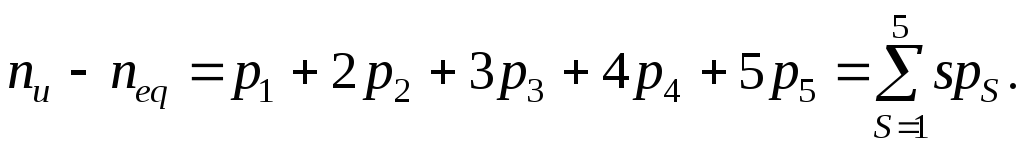(4.9)

При такой постановке задачи силового расчета число неизвестных всегда больше числа уравнений, что делает эту задачу неразрешимой. Она тем более неразрешима, если в механизме имеются избыточные связи, поскольку при этом число неизвестных реакций возрастает, а число уравнений остается неизменным.

Для того, чтобы задача стала разрешимой, необходимы дальнейшие уточнения физической модели, введение дополнительных предположений о свойствах кинематических пар. Одно из таких уточнений заключается в предположении о том, что все кинематические пары осуществляют идеальные связи. При идеальных связях работа сил реакций каждой кинематической пары должна равняться нулю при любом возможном перемещении, т.е. должно быть

(4.10)

Здесь – малые возможные перемещения вдоль осей координат, а – малые повороты вокруг этих осей. Вращательная пара (см. рис.4.1) допускает только малый поворот звена 2 (цапфы) относительно звена 1 (втулки) вокруг оси 0z. Тогда из (4.10) имеем

Поскольку при повороте , имеем Таким образом, одна из шести компонент реакций вращательной пары определилась, и число неизвестных уменьшилось на единицу – степень подвижности пары.

В поступательной паре возможное перемещение ползуна относительно направляющей направлено вдоль оси х. Поэтому здесь и поскольку имеем , что также определяет одну из неизвестных компонент реакций.

В цилиндрической паре отличны от нуля возможные перемещения (поворот вокруг продольной оси 0z) и (перемещение вдоль этой оси), так что здесь

В силу независимости возможных перемещений и это условие должно выполняться как при так и при . Это приводит к выводу о том, что R_Z и должны равняться нулю, что определяет для двухподвижной цилиндрической пары две компоненты реакций.

Аналогично можно показать, что в любой s–подвижной паре условие идеальности приводит к появлению s дополнительных соотношений для компонент реакций. В результате для механизма в целом появляется условий, что делает задачу силового расчета разрешимой. Часто в этом случае говорят о статической определимости механизма.

В тех случаях, когда учет трения становится необходим, приходится существенно изменять постановку задачи, о чем будет подробно рассказано ниже.

4.2. Уравнения кинетостатики. Определение главного вектора и главного момента сил инерции

Уравнения (4.7) удобно представить в другой форме. Введем в рассмотрение силы инерции материальных точек s–го звена

(4.11)

где – масса i–й материальной точки; – ее ускорение. Напомним, что «сила инерции» лишь условно называется силой; в действительности это мера движения материальной точки, подобная, например, количеству движения. Вводя силы инерции, можно преобразовать левые части уравнений (4.7); учитывая, что , получаем

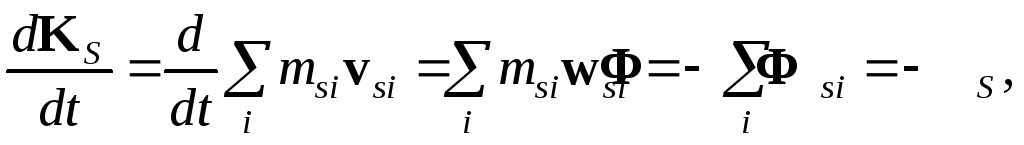(4.12)

(4.13)

Здесь – главный вектор сил инерции s–го звена, а – их главный момент относительно некоторой произвольно выбранной точки О.

В правых частях уравнений (4.7) выделим активные силы и реакции кинематических пар :

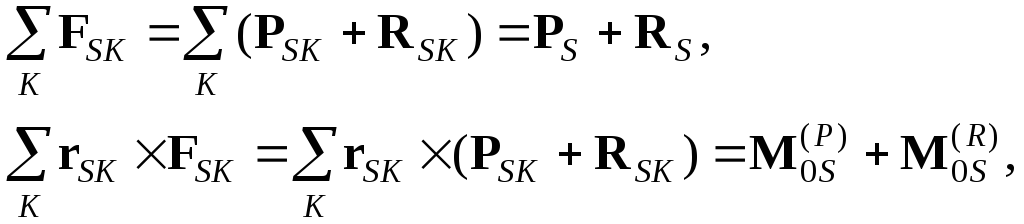¹ (4.14)

где и – главные векторы активных сил и реакций связей, действующих на s–е звено, и – их главные моменты относительно точки О. Подставив (4.14) в (4.7), получим уравнения движения в следующей форме:

. (4.15)

Уравнения движения получили форму уравнений равновесия. Можно сказать, исходя из этой формы, что активные силы, действующие на каждое из подвижных звеньев механизма, реакции связей и силы инерции звена образуют уравновешенную систему. Следует только помнить об условности такой формулировки; в действительности силы инерции силами не являются; они являются мерами движения. Соответственно уравнения (4.15) являются уравнениями движения, а не уравнениями равновесия. Чтобы подчеркнуть это обстоятельство, их называют уравнениями кинетостатики, а модель силового расчета механизма, основанную на их применении, – кинетостатической моделью.

Для составления уравнений в форме (4.15) необходимо уметь определять главные векторы и главные моменты сил инерции звена при заданном законе его движения. Выражения для и в общем случае движения твердого тела выводятся в курсах аналитической механики². Пусть некоторая точка О (рис.4.2) выбрана за полюс звена, – вектор, определяющий положение его центра масс С.

Если известны ускорение полюса , вектор угловой скорости звена и вектор его углового ускорения (они определяются при кинематическом анализе механизма), то для главного вектора сил инерции и для главного момента их относительно точки О справедливы следующие выражения:

(4.16)

(4.17)

Здесь m – масса звена, I₀ – тензор инерции в точке О. Если ввести систему координат 0хyz, связанную со звеном, то тензор I₀ можно задавать матрицей моментов инерции

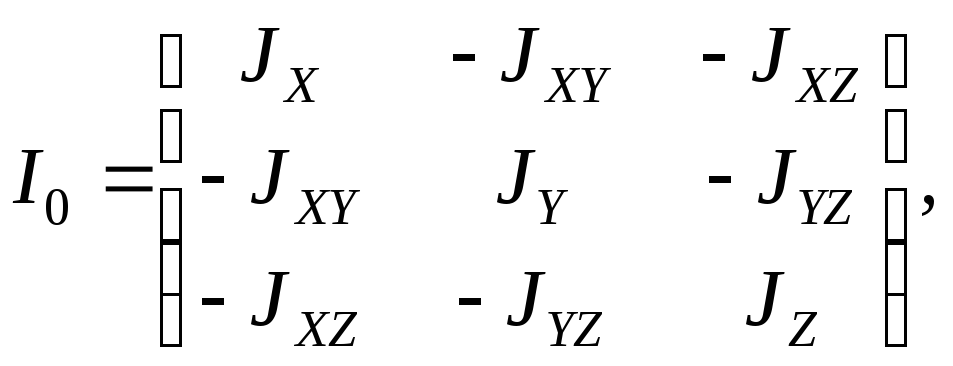(4.18)

где J_X, J_Y, J_Z – осевые, а J_XY, J_YZ, J_XZ – центробежные моменты инерции. Найдем выражения для проекций на оси главного вектора и главного момента сил инерции в некоторых частных случаях.

a). Поступательное движение звена. Учитывая, что ω=0, ε=0, найдем :

Здесь х_с, y_c, z_c – координаты центра масс. Тогда:

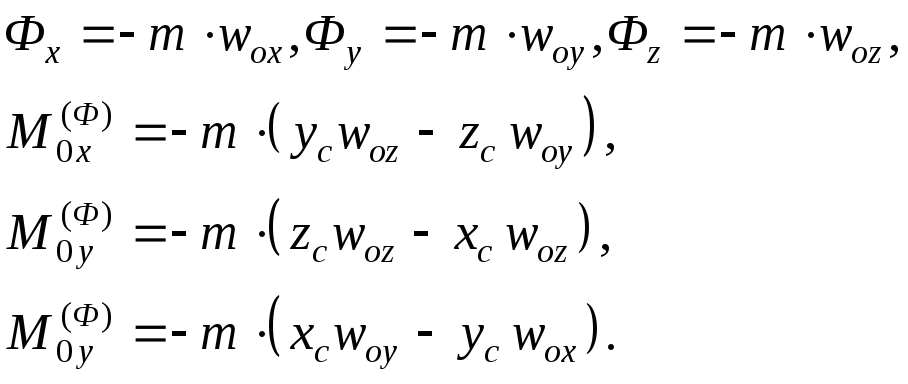(4.19)

б). Вращение вокруг неподвижной оси (рис.4.3).

Здесь

ω_х = ω_y = 0; ω_z = ω; ε_x = ε_y = 0; ε_z = ε; w₀ = 0.

Для определения главного вектора сил инерции найдем векторные произведения:

,

.

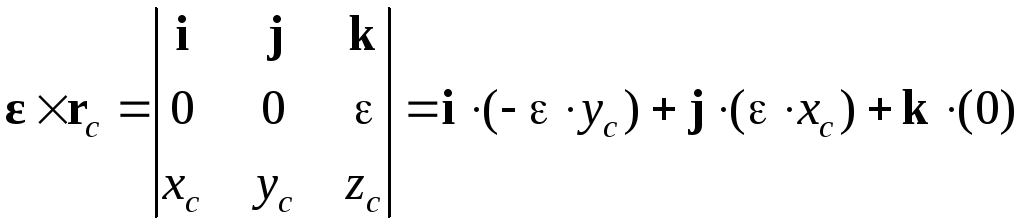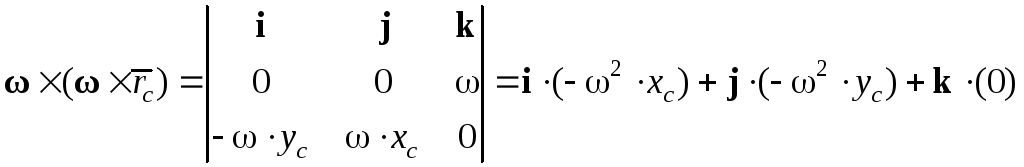Отсюда найдем проекции главного вектора сил инерции:

(4.20)

Для определения главного момента сил инерции найдем I₀ и :

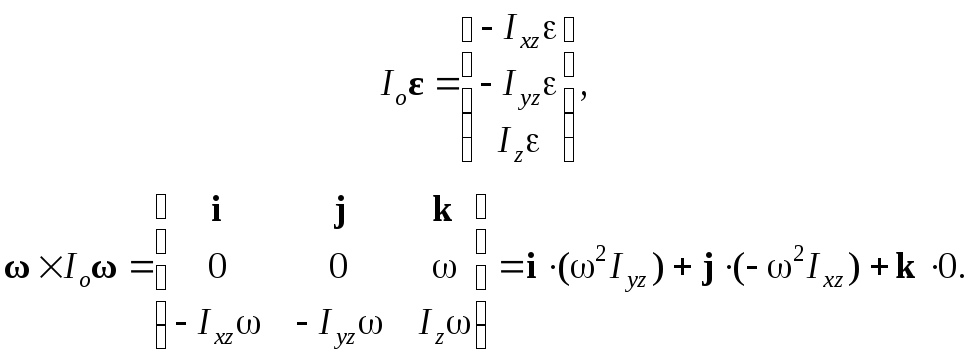
Подставляя найденные соотношения в выражение (4.17), найдем главный момент сил инерции в проекциях на координатные оси:

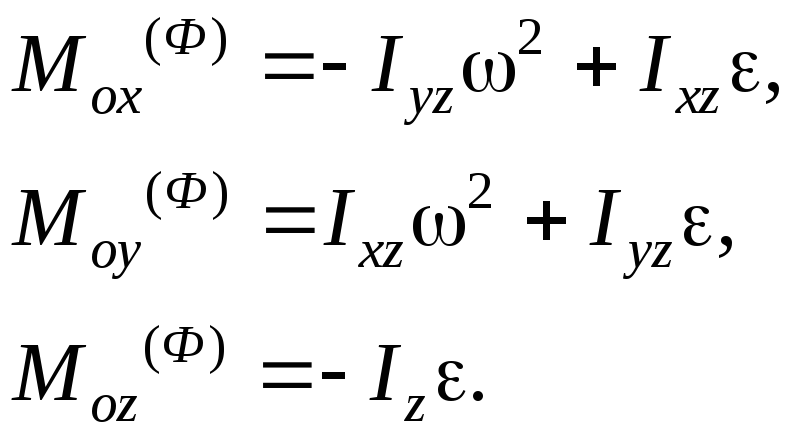(4.21)

в). Плоское движение звена. Выберем в качестве полюса центр масс звена С. Введем систему координат Сxyz так, чтобы ось Сz была перпендикулярна плоскости движения звена. В осях Cxyz построим тензор инерции I_С:

.

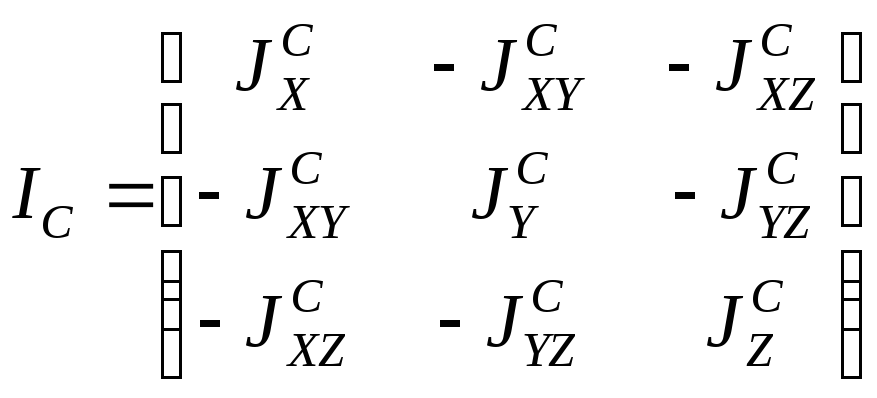Тогда получим следующие выражения для главного вектора и главного момента сил инерции:

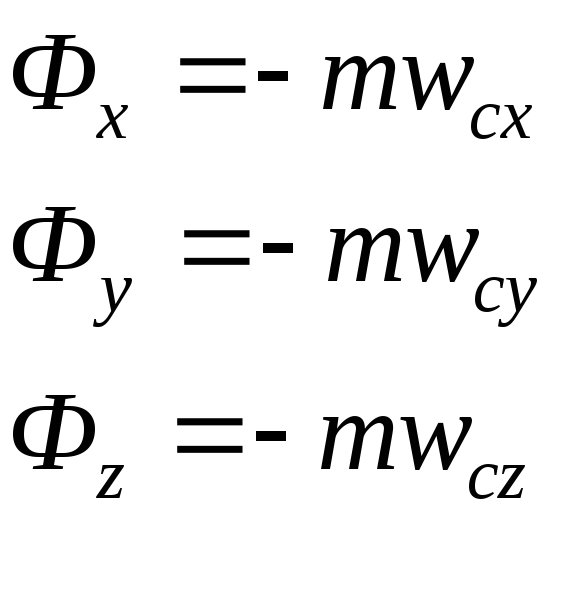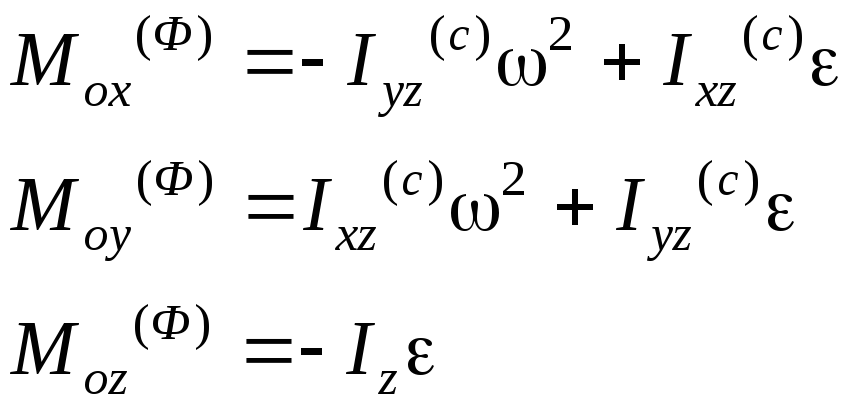, (4.22)

1 Следует различать обозначения: – главный момент сил реакций в кинематической паре и – главный момент сил реакций, действующий на s –е звено.

2 Лурье А.И. Аналитическая механика. М.: Физматгиз, 1961. 824 с.

131