
-
Геометрический анализ исполнительных механизмов промышленных роботов
Рассмотрим пространственный механизм со структурой «дерева». Такие модели используется для описания исполнительных механизмов промышленных роботов, грузоподъемных механизмов и т.п. (см., например, рис. 1.11 ).
 Для
построения функции положения воспользуемся
следующим методом. Свяжем с некоторым
s-м
звеном исполнительного механизма
систему координат 0sxsyszs,
а со звеном (s–1)
– систему координат 0s-1xs-1ys-1zs-1
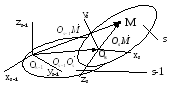
(рис.2.13). Составим вспомогательную
табличку, в которой укажем косинусы
углов между осями s-й
и (s–1)-й
системами координат (табл. 2.1):
Для
построения функции положения воспользуемся
следующим методом. Свяжем с некоторым
s-м
звеном исполнительного механизма
систему координат 0sxsyszs,
а со звеном (s–1)
– систему координат 0s-1xs-1ys-1zs-1
(рис.2.13). Составим вспомогательную
табличку, в которой укажем косинусы
углов между осями s-й
и (s–1)-й
системами координат (табл. 2.1):
Таблица 2.1
|
|
Xs |
Ys |
Zs |
|
Xs-1 |
Cos(Xs-1,Xs) |
Cos(Xs-1,Ys) |
Cos(Xs-1,Zs) |
|
Ys-1 |
Cos(Ys-1,Xs) |
Cos(Ys-1,Ys) |
Cos(Ys-1,Zs) |
|
Zs-1 |
Cos(Zs-1,Xs) |
Cos(Zs-1,Ys) |
Cos(Zs-1,Zs) |
Обычно для краткости эти косинусы обозначают буквами (табл. 2.2):
Таблица 2.2
|
|
Xs |
Ys |
Zs |
|
Xs-1 |
11 |
12 |
13 |
|
Ys-1 |
21 |
22 |
23 |
|
Zs-1 |
31 |
32 |
33 |
Элементы этой таблицы имеют следующие свойства:
-
Сумма квадратов косинусов в каждой строке равна единице, т.е.
211 + 212 + 213 = 1;
221 + 222 + 223 = 1;
231 + 232 + 233 = 1;
-
Сумма попарных произведений равна 0, т.е.
11 21+ 1222 + 1323 = 0;
21 31+ 2232 + 2333 = 0;
11 31+ 1232 + 1333 = 0.
Таким образом, все элементы таблицы не являются независимыми, и их можно выразить через три параметра, например, через углы Эйлера.
Положение
s-й
системы координат относительно (s–1)-й
определяется вектором
![]() ,
связывающим начала систем координат,
и матрицей
направляющих косинусов
Аs-1,s,
полученной из таблицы направляющих
косинусов:
,
связывающим начала систем координат,
и матрицей
направляющих косинусов
Аs-1,s,
полученной из таблицы направляющих
косинусов:
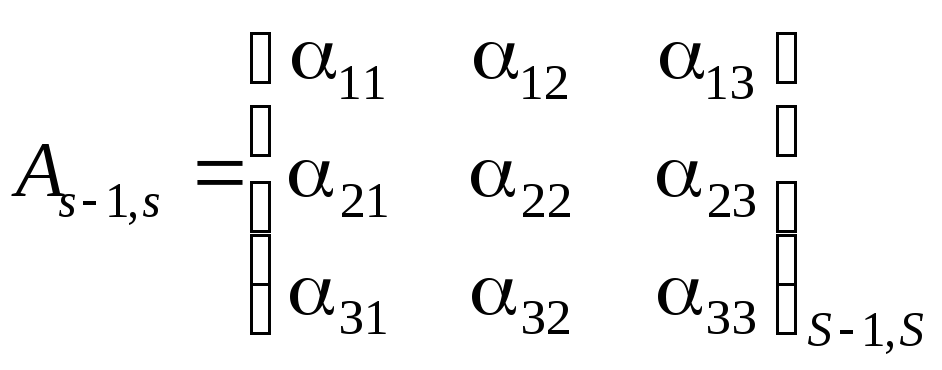 .
(2.39)
.
(2.39)
Матрицы Аs-1,s обладают важным свойством. Если Аs-1,s и Аs,s+1 – матрицы направляющих косинусов между осями соответственно (s–1)-й и s-й (первая) и s-й и (s+1)-й (вторая) систем координат, то
Аs-1,s+1 = Аs-1,s Аs,s+1 . (2.40)
Пусть
на s-м
звене имеется некоторая точка М.
Соединив ее с точками 0s-1
и 0s,
построим векторы
![]() и
и
![]() .
Для них можно записать следующее
векторное равенство:
.
Для них можно записать следующее
векторное равенство:
![]() .
(2.41)
.
(2.41)
Вектор
![]() может быть задан проекциями на оси
какой-либо системы координат, например,
(s–1)-й:
может быть задан проекциями на оси
какой-либо системы координат, например,
(s–1)-й:
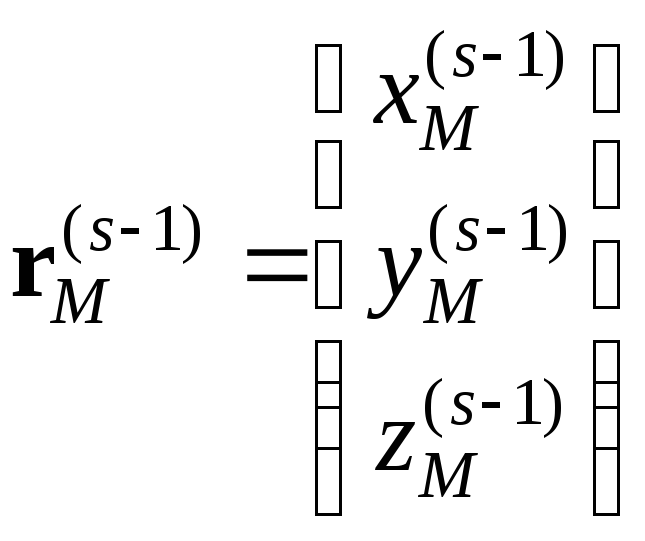 .
(2.42)
.
(2.42)
Аналогично
можно задать вектор
![]() проекциями на оси s-й
системы координат:
проекциями на оси s-й
системы координат:
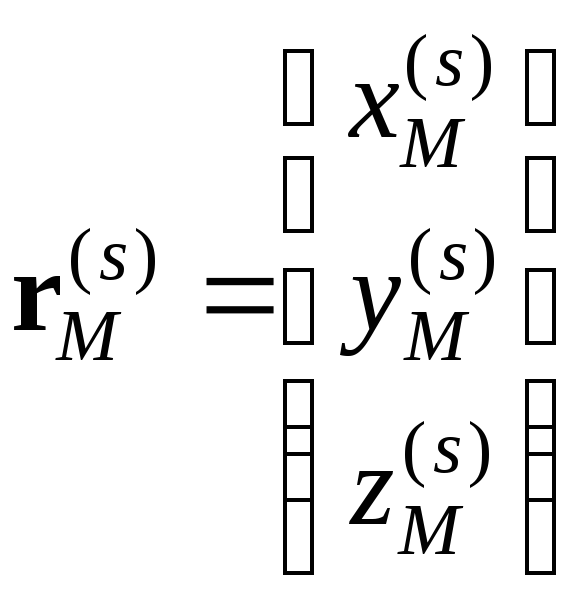 ,
(2.43)
,
(2.43)
а
вектор
![]() – проекциями на оси (s–1)-й
системы координат:
– проекциями на оси (s–1)-й
системы координат:
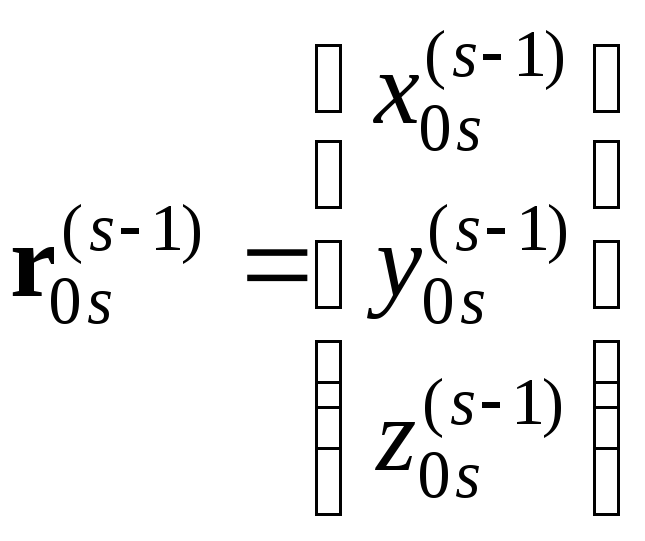 .
(2.44)
.
(2.44)
Используя представления (2.42–2.44), можно записать выражение (2.41) в проекциях на оси (s–1)-й системы координат:
![]() (2.45)
(2.45)
Из (2.45) следует, что, если нам известно положение точки М на s-м звене и положение s-го звена относительно (s–1)-го, то можно получить координаты точки М на (s–1)-м звене. Перемещаясь далее к (s–2)-му , (s–3)-му и т.д. звеньям, можно дойти до стойки и получить координаты точки М в неподвижной системе.
В соотношении (2.45) есть некоторое неудобство, заключающееся в том, что операция умножения матриц чередуется с операцией сложения. Для того, чтобы оставить только операции умножения матриц, обычно вводят четырехмерные векторы-столбцы координат:
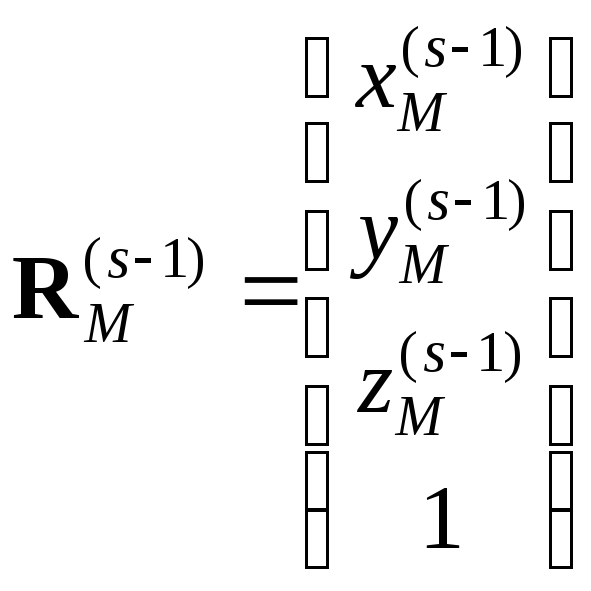 ,
,
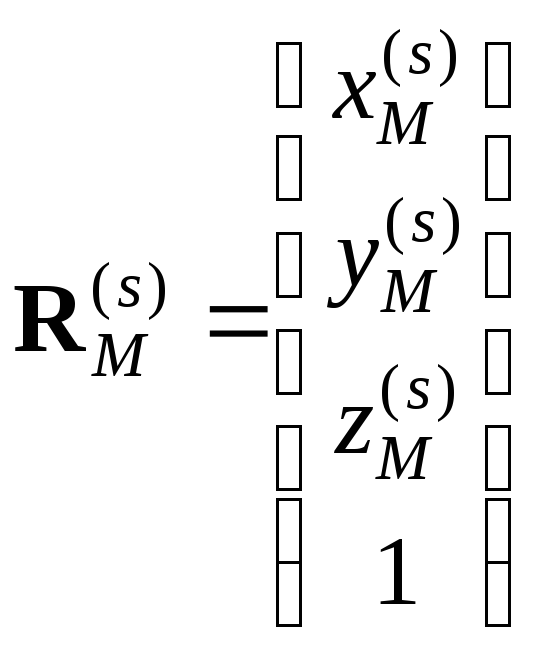 , (2.46)
, (2.46)
а также блочные матрицы 4х4:
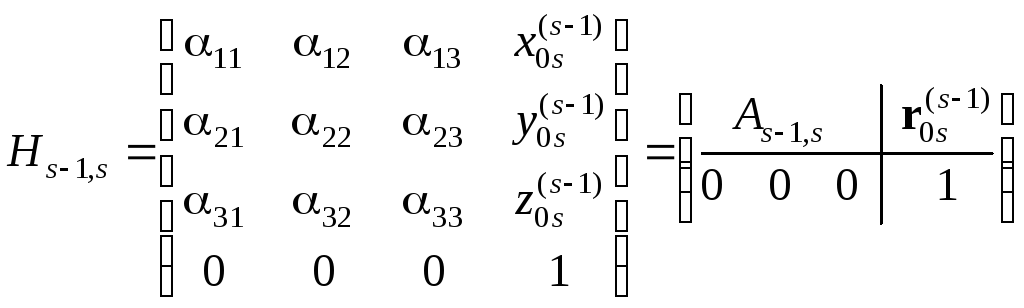 .
(2.47)
.
(2.47)
Матрицы Hs-1,s называются матрицами перехода от s-й системы координат к (s–1)-й системе. Тогда соотношение (2.45) можно записать в виде:
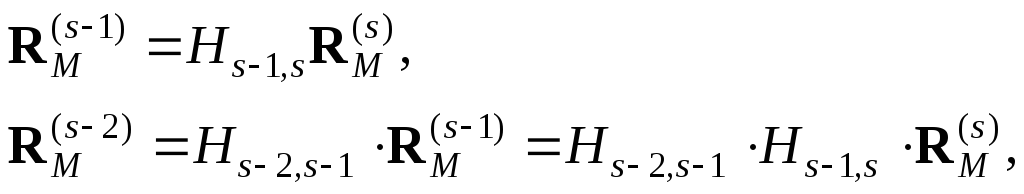 (2.48)
(2.48)
и т.д.
Перемножая последовательно матрицы перехода, можно дойти до неподвижной системы координат:
![]() .
(2.49)
.
(2.49)
Здесь
![]() – вектор-столбец координат точки М
в системе, связанной со звеном n,
а
– вектор-столбец координат точки М
в системе, связанной со звеном n,
а
![]() – вектор-столбец координат точки М
в неподвижной системе. Таким образом,
выражение (2.49) дает возможность построить
функцию положения некоторой точки в
явном виде. Для того, чтобы это сделать,
нужно составить матрицы перехода.
Рассмотрим подробнее матрицы перехода
для двух наиболее часто встречающихся
видов кинематических пар – вращательной
и поступательной.
– вектор-столбец координат точки М
в неподвижной системе. Таким образом,
выражение (2.49) дает возможность построить
функцию положения некоторой точки в
явном виде. Для того, чтобы это сделать,
нужно составить матрицы перехода.
Рассмотрим подробнее матрицы перехода
для двух наиболее часто встречающихся
видов кинематических пар – вращательной
и поступательной.
