Добавил:

Xer1t Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский политехнический университет Петра Великого (бывш. СПбГПУ)

Предмет:

Теоретическая механика

Файл:

Малые колебания / Задача

.PDF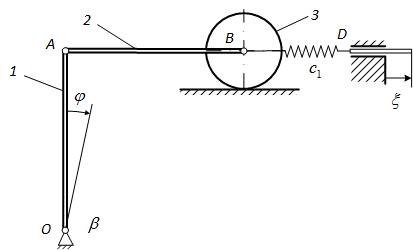

Скачиваний:

Добавлен:

26.11.2019

Размер:

411.05 Кб

Скачать

☆

Задача

Система состоит из кривошипа 1, шатуна 2, однородного цилиндра 3, катящего без скольжения по плоскости и пружины BD жѐсткости c1 (рис. 1).

Конец пружины прикреплѐн к штоку, который перемещается по законуe sin p t . Кривошип и шатун являются однородными стержнями одинаковой длинны l . При вертикальном положении стержня OA и 0

пружина BD не напряжена. При t 0 угол отклонения и скорость отклонения стержня 1 от устойчивого положения 0 равны 0 и 0 соответственно.

На кривошип 1 действует момент сопротивления Mсопр

Рис. 1

Дано: m1 m2			1, 2 кг ;		m3 1,6 кг ; l 0,3 м ; c1 840	Н / м ; 7, 2	Н м с ;
	0	0,1 рад ;		0,05	с 1 ; g 10 м / с2 ; e 0,03 м ;	p 10 с 1 .
	0		0

Определить вынужденные колебания стержня.

Решение:

Составим расчѐтную схему согласно заданным параметрам (рис. 2). Система имеет одну степень свободы. В качестве обобщѐнной координаты

выберем угол поворота стержня 1 (положительное направление по часовой стрелке). Введѐм горизонтальную координату центра тяжести (точки B) цилиндра 3 - x3 (от равновесного положения) и угол поворота цилиндра 3 -

3 , а так же угол поворота стержня 2 - 2 . В положении равновесия имеем

0 , x3 0 , 3 0 , 0 .

Обозначим все учитываемые силы и моменты в системе:


- силы тяжести m1g	, m2 g	, m3 g	;

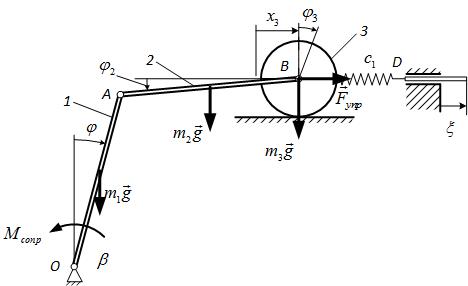
- сила упругости пружины Fупр ; - момент сопротивления Mсопр .

Рис. 2

Предварительно определим геометрические и кинематические зависимости в системе, предполагая, что отклонения стержня 1 от положения равновесия невелики.

Имеем геометрические связи:

x3	l l sin l cos 2 ;
	(1)
l l cos l sin 2 ;
Дифференцируя по времени:
x3	l cos l sin 2 2 ;

0 l sin l cos 2 2 ;

(2)

Учитывая малые отклонения от положения равновесия, при которых имеем приближѐнные равенства sin , sin 2 2 , cos 1 12 2 ,

cos 2 1					1	2			2 и пренебрегая степенями более второй, из второго
cos 2 1					2	2			2 и пренебрегая степенями более второй, из второго
					2
уравнения системы (1) получаем:
	sin 2 1 cos 1																	1		2				1			2
2														1															;
2														1				2						2					;
																		2						2
x3 l sin l cos 2 l l l																								1				2
																				1						2			l				(3)
																				1				2		2			l				(3)
																								2
			1	1			2	2					1			4
l								l									l		;
l			2					l					8				l		;
			2	2									8
Аналогично из (2):
2		sin																															;

		cos 2						1		1	2	2							1	1					2 2					1	1	4
		cos 2																	1	1					2 2
																1
									2							1														8
									2										2	2										8
																			2	2
				1		2		l 2 2							l 1						2		;
x3	l 1
x3	l 1			2
				2
																						2				, имеем скоростей:
Пренебрегая произведениями и																										, имеем скоростей:
2	0;																																(4)
x3	l ;																																(4)
x3	l ;

Для модуля скорости центра тяжести стержня 2, рассматривая его движение как вращение относительно движущейся точки B и учитывая (4), имеем:

	2	l		2
V2	x3			2	x3 l	(5)
			2

Учитывая (4) (угловая скорость стержня приблизительно равна нулю), движение стержня 2 можно приближѐнно рассматривать как поступательное со скоростью (5).

Цилиндр 3 совершает сложное движение, при котором скорость точки касания его с поверхностью равна нулю.

Таким образом, точка касания с поверхностью является мгновенным центром скоростей для цилиндра. Учитывая это, скорость центра колеса равна:

x3 r 3

Откуда, учитывая (4), угловая скорость цилиндра 3:

	1		l	(6)

3	r	x3	r

Далее, для решения задачи составим уравнение Лагранжа второго рода, которое в нашем случае, учитывая, что на систему действуют консервативные силы (сила тяжести), диссипативные силы (момент сопротивления) и возмущающая сила (сила упругости), имеет вид:

	d	T	T		QF
						(7)

	dt
Где T T1 T2 T3				- кинетическая энергия системы; - функция рассеяния

системы (диссипативная функция Релея); QF - обобщѐнная возмущающая сила.

Кинетическая энергия стержня 1 при вращении вокруг неподвижной оси равна:

T1 12 JO 2

Где момент инерции стержня относительно оси точки O равен:

J			1	m l2											(8)
J	O			m l2											(8)
	O	3			1
		3
Таким образом, получаем:
		1			1			2	2	1		2		2
T1						m1	l				l				(9)
T1		2			3	m1	l			6	l		m1		(9)
		2			3					6

Кинетическая энергия стержня 2, движущегося приблизительно поступательно, учитывая (5), равна:

	1	2	1		2	1		2		2
T2		m2 V2					l				(9)
T2	2	m2 V2	2	m2 l		2	l		m2		(9)
	2		2			2

Кинетическая энергия цилиндра 3, совершающего сложное плоскопараллельное движение, равна:

T3 12 m3 x32 12 J3 32

Момент инерции цилиндра 3 относительно центра тяжести как однородного цилиндра равен:

J		1	r2 m	(10)
	3
		2	3

Таким образом, кинетическая энергия, учитывая (4), (6), (10):

	1		2	1	1		2		l	2	3		2		2
T3						r		m3				l				(11)
	2	m3 l		2	2						4			m3
									r

Кинетическая энергия системы:

T			1	l2 m 2				1	l2		m 2		3	l2 m 2
T				l2 m 2					l2		m 2			l2 m 2
		6				1	2				2		4	3
		6					2						4		(12)
	1				1					3					(12)
	1			2	1					3		2
		l				m1 m2					m3
	2	l				m1 m2				2	m3
	2				3					2

Найдѐм производные от кинетической энергии, входящие в уравнение (7):

d	T		2	1
		l			m1	m2
				3
dt

3	m3		T	0	(13)

2		;

Потенциальную энергию системы определим, как работу сил тяжести перемещению системы из некоторого положения в нулевое (положение равновесия).

Потенциальная энергия системы, учитывая (3), равна:

m1 g			l		1 cos m2				g	l	sin 2

			2						2				(14)
		l		1			l	1				l
m1	g				2 m2	g			2				m1 m2 g 2
			2					2
	2					2					4

Найдѐм производную потенциальной энергии, входящую в уравнение (7):

l	m m		g

2	1	2

Функция рассеяния системы, равна:

12 2

Производная функции рассеяния:



Обобщѐнная вынуждающая сила, учитывая растяжение пружины равна:

QF	Fупр	x3	c1	x3	l	l c1 e sin p t l

Таким образом, подставляя (13), (15), (17) и (18) в (7), получаем:

(15)

(16)

(17)

x3 ,

(18)

m1 m2

l c1

e sin p t

Это уравнение является уравнением вынужденных колебаний системы с линейным сопротивлением.

В каноническом виде:
2 n k		h sin p t	(19)
	2

Где

- коэффициент затухания:

n												7,2			10	с 1	(20)

			1			3					1		3
		2	1			3		2			1		3
	2 l			m1	m2		m3		2 0,3			1,2 1,2		1,6
	2 l		3	m1	m2	2	m3		2 0,3			1,2 1,2	2	1,6
			3			2				3			2

- круговая частота без учѐта сопротивления:

		l c			1	m m			g		0,3 840					1	1,2 1,2 10
		l c				m m			g		0,3 840						1,2 1,2 10
k			1	2		1		2							2						14,142 с 1
				2											2								(21)
			1				3					1						3					(21)
			1				3					1						3
		l		m1		m2			m3			0,3		1,2 1,2					1,6
		l	3	m1		m2	2		m3			0,3	3	1,2 1,2				2	1,6
			3				2						3					2
- относительная амплитуда возмущающей силы:
h						c1 e									840 0,03							21 с 2	(22)
h		1						3					1						3			21 с 2	(22)
		1						3					1						3
	l			m1		m2				m3		0,3			1, 2 1, 2					1,6
	l			m1		m2		2		m3		0,3	3		1, 2 1, 2				2	1,6
		3						2					3						2

Уравнение (19) имеет общее решение, состоящее из общего решения * соответствующего однородного уравнения:

2 n k			0	(23)
		2

и частного решения уравнения ** (19).

Таким образом, имеем:

* **	(24)
Характеристическое уравнение для (23) имеет вид:
2 2 n k 2 0	(25)
Откуда корни его равны:

	n	n2 k 2
1,2

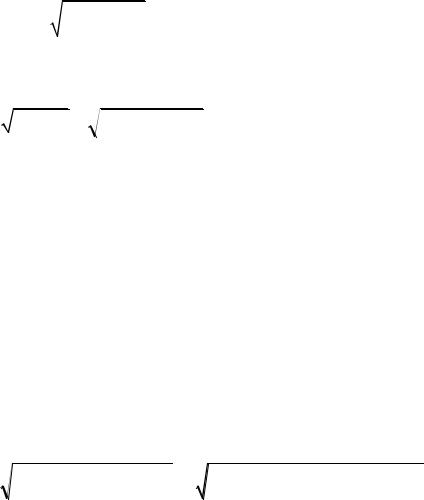
Так как в нашем случае имеем n k , то

1,2 n 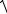k2 n2 n k1 i

Где круговая частота собственных колебаний системы равна:

k1 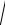k2 n2 14,1422 102 10 с 1

Общее решение однородного уравнения (23) имеет вид:

* e n t C1 cos k1 t C2 sin k1 t

Частное решение уравнения (19) имеет вид:

** A sin p t

Подставляя его в (19), находим значения:

- амплитуды вынужденных колебаний

A			h				21


			2 4					2 4 102
		p2		n2	p2		102		102
	k 2	p2		n2	p2	14,1422	102		102

0,094 рад

-сдвиг фазы вынужденных колебаний

2 n p

2 10 10

arctg

1,107 рад

14,142

Получаем общее решение уравнения (19):

e n t C1 cos k1 t C2 sin k1 t A sin p t

Производная по времени:

n t

k1 n C1 cos k1 t n C2

C1 k1 sin k1 t

A p cos p t

(26)

(27)

(28)

(29)

(30)

(31)

(32)

Определяем постоянные интегрирования из начальных условий:

e n 0 C1 cos k1 0 C2

sin k1 0 A sin p 0

A sin ;

(33)

n 0

C2 k1 n C1 cos k1 0 n C2 C1 k1 sin k1

A p cos p 0 C2

n C1 A p cos ;

Откуда:

C1 0

A sin 0,1 0,094 sin 1,107 0,184 рад;

(34)

0 n 0 n A sin A p cos

0,05 10 0,15 10 0,094 sin 1,107

0,147 рад;

0,094 10 cos 1,107

Таким образом, получаем искомую зависимость:

e 10 t 0,184 cos 10 t 0,147 sin 10 t 0,094 sin 10 t 1,107

Ответ:

e 10 t 0,184 cos 10 t 0,147 sin 10 t 0,094 sin 10 t 1,107

Соседние файлы в папке Малые колебания

#
26.11.2019210.94 Кб5Задача.doc
#
26.11.2019411.05 Кб9Задача.PDF