Малые колебания / Задача

Задача

Рис. 1

Дано: ; ; ; ; ; ; ; ; ; .

Решение:

В качестве обобщённой координаты выберем угол поворота стержня 1 (положительное направление по часовой стрелке).

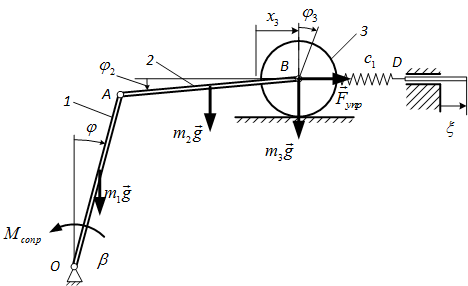
Рис. 2

Учитывая малые отклонения от положения равновесия, при которых имеем приближённые равенства , , ,

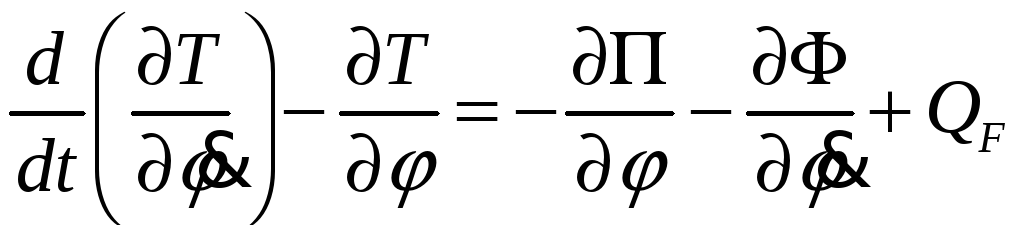(7)

Где - кинетическая энергия системы; - диссипативная функция Релея; - обобщённая возмущающая сила.

Кинетическая энергия стержня 1 при вращении вокруг неподвижной оси равна:

Где момент инерции стержня относительно оси точки равен:

(8)

Таким образом, получаем:

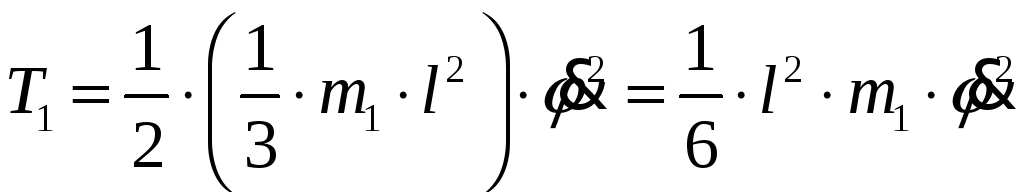(9)

Кинетическая энергия стержня 2, движущегося приблизительно поступательно, учитывая (5), равна:

(9)

Кинетическая энергия цилиндра 3, совершающего сложное плоскопараллельное движение, равна:

Момент инерции цилиндра 3 относительно центра тяжести как однородного цилиндра равен:

(10)

Таким образом, кинетическая энергия, учитывая (4), (6), (10):

(11)

Кинетическая энергия системы:

(12)

Найдём производные от кинетической энергии, входящие в уравнение (7):

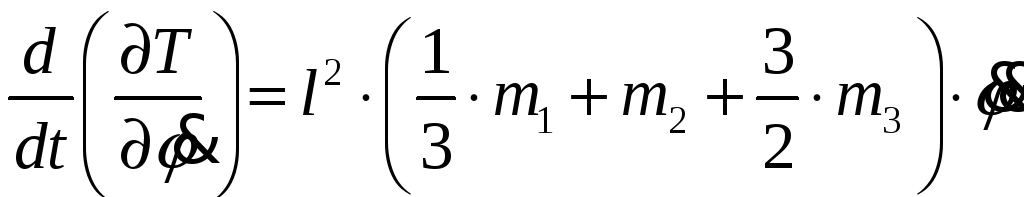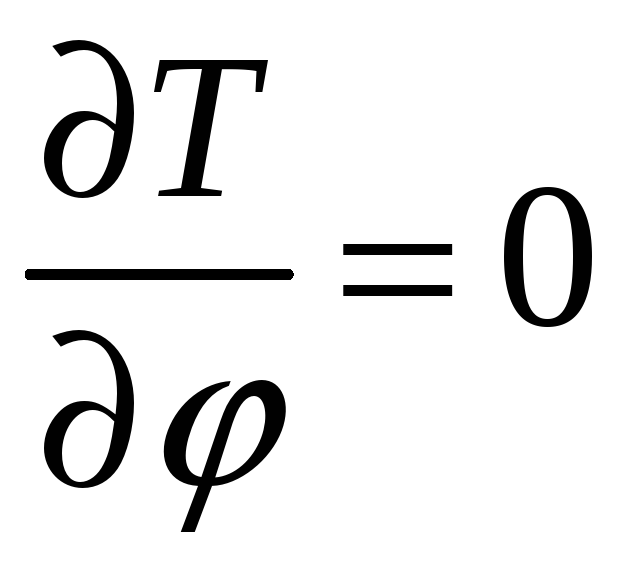; (13)

Потенциальную энергию системы определим, как работу сил тяжести перемещению системы из некоторого положения в нулевое (положение равновесия).

Потенциальная энергия системы, учитывая (3), равна:

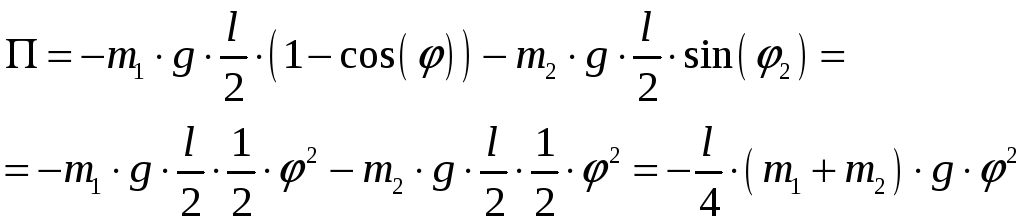(14)

Найдём производную потенциальной энергии, входящую в уравнение (7):

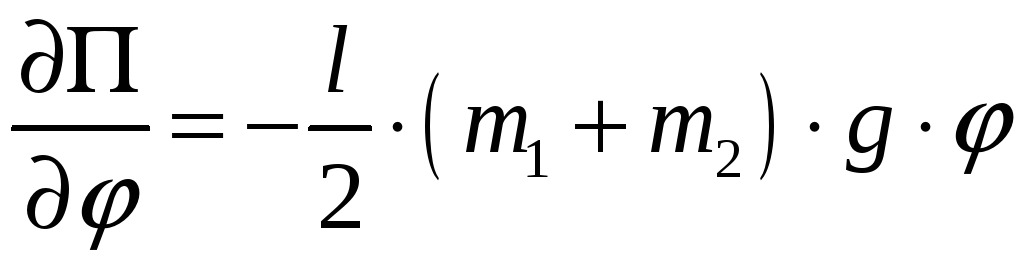(15)

Функция рассеяния системы, равна:

(16)

Производная функции рассеяния:

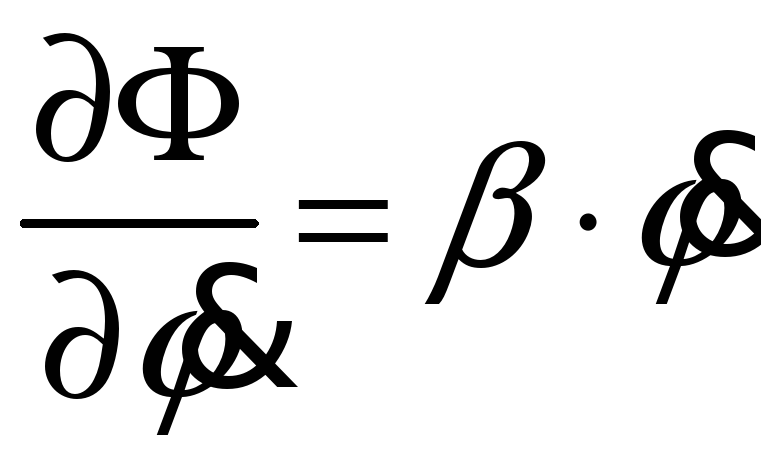(17)

Обобщённая вынуждающая сила, учитывая растяжение пружины , равна:

(18)

Таким образом, подставляя (13), (15), (17) и (18) в (7), получаем:

Это уравнение является уравнением вынужденных колебаний системы с линейным сопротивлением.

В каноническом виде:

(19)

Где

- коэффициент затухания:

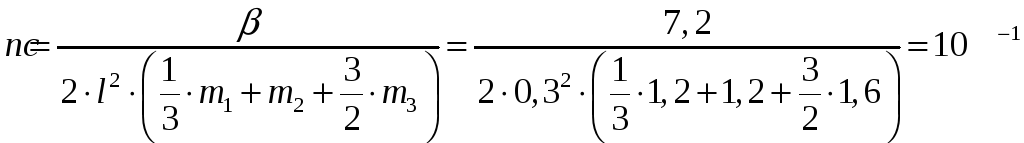(20)

- круговая частота без учёта сопротивления:

(21)

- относительная амплитуда возмущающей силы:

(22)

Уравнение (19) имеет общее решение, состоящее из общего решения соответствующего однородного уравнения:

(23)

и частного решения уравнения (19).

Таким образом, имеем:

(24)

Характеристическое уравнение для (23) имеет вид:

(25)

Откуда корни его равны:

Так как в нашем случае имеем , то

Где круговая частота собственных колебаний системы равна:

(26)

Общее решение однородного уравнения (23) имеет вид:

(27)

Частное решение уравнения (19) имеет вид:

(28)

Подставляя его в (19), находим значения:

- амплитуды вынужденных колебаний

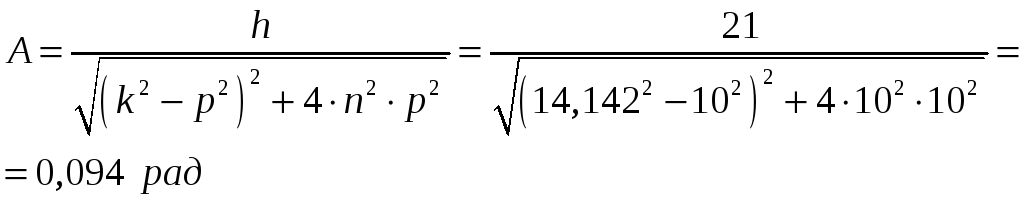(29)

- сдвиг фазы вынужденных колебаний

(30)

Получаем общее решение уравнения (19):

(31)

Производная по времени:

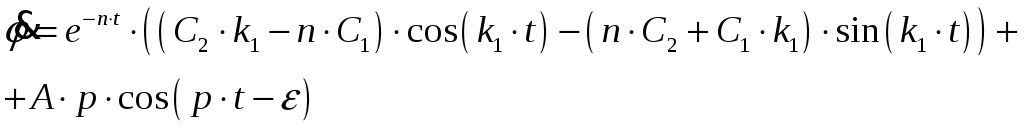(32)

Определяем постоянные интегрирования из начальных условий:

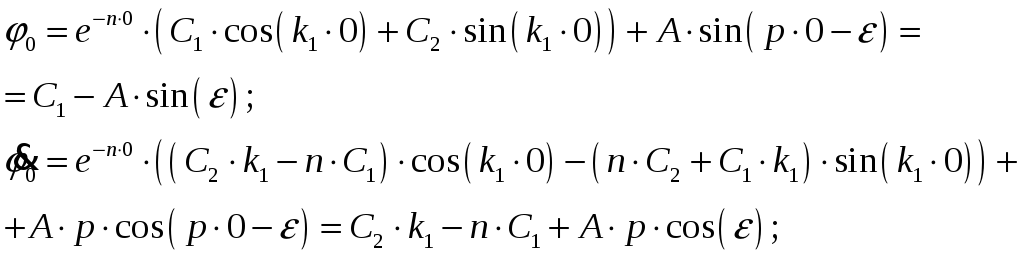(33)

Откуда:

(34)

Таким образом, получаем искомую зависимость:

Ответ: