
ЭКЗ / tmm_chapter8
.pdfГЛАВА 6. УРАВНЕНИЯ ДВИЖЕНИЯ МЕХАНИЗМА
СЖЕСТКИМИ ЗВЕНЬЯМИ
6.1.Уравнения Лагранжа второго рода для механизма с одной степенью подвижности
Уравнение Лагранжа второго рода для механической системы
d T |
|
T |
Q Q |
, |
||
|
|
|
|
|||
|
|
|
q |
C |
||
dt q |
|
|
|
|||
Т(q, q ) – кинетическая энергия механизма; Q – обобщенная движущая сила;
N |
|
|
|
|
QC PCi |
rCi M0(PiC ) i |
|||
i 1 |
|
q |
q |
|
QС– обобщенная сила сопротивления.
В механизме с одной степенью подвижности
T 12 a(q)q2 .
a(q) m(q) – приведенная масса или приведенный момент инерции
(6.1)
(6.2)
(6.3)
(q –
линейная или угловая обобщенная координата).
В дальнейшем будет предполагаться, что q – угловая координата, и выражение (6.3) записывается в форме
|
|
|
|
|
|
|
|
T |
1 |
|
|
2 |
, |
|
|
(6.4) |
||
|
|
|
|
|
|
|
|
2 |
J (q)q |
|
|
|||||||
J(q) – приведенный момент инерции. |
|
|
|
|
|
|
|
|
||||||||||
T |
|
1 |
|
2 |
, |
|
d T |
|
d |
|
|
|
|
|
2 |
|
||
|
|
|
|
|
|
|
|
|
||||||||||
q |
2 |
J (q)q |
|
|
dt |
J (q) q J (q)q |
J (q)q, |
|||||||||||
|
|
|
|
|
dt q |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
J |
|
|
1 |
|
|
|
2 |
Q QC . |
|
(6.5) |
||||
|
|
|
|
(q)q |
2 |
J (q)q |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
171
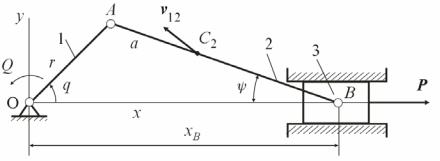
Пример составления уравнений движения механизмов.
Рис. 6.1
Для вращающегося звена 1 :
T1 12 J10 q2 ,
где J10 – момент инерции звена относительно оси вращения. Для поступательно движущегося ползуна 3:
T3 12 m3 xB2 .
Для звена 2, совершающего сложное движение (теоремоаКёнига):
T2 12 (m2vC2 2 J2C 22 ),
m2 – масса звена,
J2C – его момент инерции относительно оси, проходящей через центр масс С2;
vC2 – скорость центра масс;2 – угловая скорость.
|
|
|
|
|
dx |
B |
|
|
|
|
2 |
dx |
|
2 |
dy |
|
2 |
2 |
|
|
|
|
|
|
|
d |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
C 2 |
|
|
|
C 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
dq |
|
|
dq |
|
|
|
; 2 |
|
|
|
|
|
|
||||||||||||||
|
|
xB |
dq |
|
|
q;vC 2 |
|
|
q |
|
|
dq q, |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где – угол поворота звена 2, получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
T T1 T2 T3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 |
|
dx |
|
|
|
|
|
2 |
dy |
|
2 |
|
|
2 |
d |
2 |
|
dx |
|
|
2 |
|
|
2 1 |
|
2 (6.6) |
|||||||||
|
|
|
2 |
|
|
|
|
|
|
|
B |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
C |
|
|
|
|
C 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
J10 m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
JC |
|
|
|
m3 |
|
|
|
|
q |
|
|
J (q)q . |
||||||
2 |
|
dq |
|
|
|
|
dq |
|
|
|
|
|
2 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dq |
|
|
|
dq |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выражение, стоящее в фигурных скобках, представляет собой приведенный момент инерции механизма J(q). Используя функции положения xC2(q), yC2(q),(q), xB(q), можно было бы представить J(q) в явной форме.
J(q) – периодическая функция с периодом 2 ; она представима в виде ряда:
|
|
|
J (q) J0 (JC |
cos q JS sin q). |
(6.7) |
1
172
Можно записать коэффициенты Фурье через дискретные значения периодической функции:
|
|
|
1 |
|
m |
|
||
J0 |
|
|
|
|
J (2 k / m), |
|
||
|
|
|
|
|
||||
|
|
m k 1 |
|
|||||
|
|
|
|
|
2 |
m |
|
|
JC |
|
|
|
J (2 k / m)cos(2 k / m), |
(6.8) |
|||
|
|
|||||||
|
|
|
|
|
m k 1 |
|
||
|
|
|
|
|
2 |
m |
|
|
JS |
|
|
|
|
|
J (2 k / m)sin(2 k / m). |
|
|
|
|
|
|
|
||||
|
|
|
|
|
m k 1 |
|
||
Приближенное представление функций J(q) и J (q) :
|
r |
|
|
J (q) J0 (JC |
cos q JS sin q), |
(6.9) |
|
|
1 |
|
|
|
r |
|
(6.10) |
|
|
||
J (q) ( JC sin q JS cos q) . |
|||
1
Удовлетворительная аппроксимация для – й гармоники получается только при условии m 4 .
Если силами тяжести звеньев механизма можно пренебречь,
QC P |
dxB |
|
dxB |
|
dxB |
QC (q, q). |
(6.11) |
|
|
P xB (q), |
|
q |
|
||||
|
dq |
|
dq |
|
|
dq |
|
|
|
|
|
|
|||||
Обобщенная сила QС часто называется приведенным моментом сил сопротивления. Функция QС(q, q ) является также периодической по q с периодом 2 .
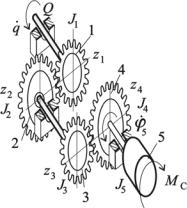
Пример механизма с линейной функцией положе-
ния.
J1, J2, J3, J4, J5 – моменты инерции вращающихся масс относительно их осей вращения;
z1, z2, z3, z4 – числа зубьев колес;
MС – момент сил сопротивления, приложенный к ротору.
В этом случае приведенный момент инерции не зависит от координаты q.
Рис. 6.2
T |
1 |
|
|
2 |
(J2 |
|
|
|
|
|
z1 |
|
2 |
(J4 |
|
|
|
|
|
z1 z3 |
|
|
2 |
|
|
|||||
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
) |
|
|
||||||||||||||
2 |
J1q |
|
J3 )( q |
z2 |
|
J5 )(q |
z2 z4 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.12) |
|||||
|
1 |
|
|
|
|
|
|
z1 |
|
|
|
|
|
|
|
|
z1z3 |
|
|
|
|
|
|
|
1 |
|
|
|
||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
2 |
|
||||||||
|
|
J1 |
(J2 J3 )( |
|
) |
|
(J4 |
J5 )( |
|
|
) |
|
|
|
|
|
|
|
|
. |
||||||||||
2 |
z2 |
|
z2 z4 |
|
q |
|
2 |
Jq |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
173
Обобщенная сила QС определяется в соответствии с (6.2): |
|
||||||||||||||||||
|
|
|
Q |
|
M |
|
|
z1z3 |
. |
|
|
|
|
|
(6.13) |
||||
|
|
|
|
C z2 z4 |
|
|
|
|
|
||||||||||
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
||||||
Уравнение движения |
|
|
|
|
|
|
|
|
|
|
z1z3 |
|
|
|
|
|
|
||
|
|
J q Q MC |
|
, |
|
|
|
|
(6.14) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
z2 z4 |
|
|
|
|
|
|
||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
z1 |
|
|
|
|
|
|
|
|
|
|
z1z3 |
|
|
|
J J |
(J |
|
J |
|
)( |
)2 |
(J |
|
J |
|
)( |
)2 |
(6.15) |
||||||
|
|
|
|
|
|
||||||||||||||
1 |
|
2 |
|
3 |
|
z2 |
|
|
|
|
4 |
|
|
5 |
|
z2 z4 |
|
||
– приведенный момент инерции механизма. Отметим, что при приведении вращающихся масс момент инерции каждой из них делится на квадрат передаточного отношения, связывающего эту массу с входным звеном.
Уравнение Лагранжа второго рода может быть использовано для определения обобщенной движущей силы Q:
|
|
2 |
|
(6.16) |
Q(t) J q(t) q(t) 0,5J |
|
q(t) q |
QC q(t), q(t),t . |
6.2. Уравнения Лагранжа второго рода для механизма с несколькими степенями подвижности
Уравнения Лагранжа второго рода для механизма с w степенями подвижности:
|
d T |
|
T |
Q |
Q |
(s = 1, … , w) , |
(6.18) |
||
|
|
|
|
|
|||||
|
|
|
|
qs |
s |
Cs |
|
|
|
|
dt qs |
|
|
|
|
|
|||
где Qs – обобщенные движущие силы; |
|
|
|||||||
|
|
|
|
|
N |
|
|
|
(6.19) |
|
|
|
QCs PCi |
rci M0( PiC ) i |
|||||
|
|
|
|
|
i 1 |
|
qs |
qs |
|
– обобщенные силы сопротивления, соответствующие всем активным силам, кроме движущих.
Кинетическая энергия каждого звена:
Ti |
1 |
mi vci2 |
Ωi(i)T JсiΩi(i) , |
(6.20) |
|
2 |
|
|
|
где i – номер звена, mi – его масса, vci – скорость центра масс, Jсi – тензор инерции в системе осей, начало которой находится в центре масс i-го звена, Ωi(i) – трехмерный вектор-столбец абсолютной угловой скорости.
174
|
Jix |
Jixy |
Jixz сi |
|
|
||||
|
Jixy |
Jiy |
|
|
|
, |
(6.21) |
||
Jсi |
Jiyz |
||||||||
|
J |
ixz |
J |
iyz |
J |
iz |
|
|
|
|
|
|
|
|
|
|
|||
где Jix, Jiy, Jiz – осевые моменты инерции i-го звена, моменты инерции, а
(i)ix
Ωi(i) i(yi) ,
iz(i)
Jixy, Jixz, Jiyz – центробежные
(6.22)
где ix(i) , iy(i) , iz(i) |
|
– проекции вектора угловой скорости i-го звена Ωi |
|
на оси i-й |
||||||||||||||||||||||||||||||||||
системы координат. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Ti |
1 |
|
|
(0) |
|
2 |
|
|
(0) |
|
2 |
|
|
(0) |
|
2 |
|
|
1 |
|
(i) |
|
2 |
|
(i) |
|
2 |
|
|
(i) |
|
2 |
|
|||||
|
mi xci |
|
|
|
yci |
|
zci |
|
|
|
|
Jix |
ix |
|
Jiy iy |
|
Jiz iz |
|
|
|||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.23) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
(i) |
|
(i) |
|
|
|
|
|
(i) |
|
|
(i) |
|
|
|
|
|
(i) |
|
(i) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2Jixy ix |
iy |
2Jixz ix |
|
iz |
2Jiyz iy |
iz . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Пример трехподвижного механизма. |
|
|
Звено 1: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T1 |
2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
2 |
J1z q1 , |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J1z – осевой момент инерции |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
q3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
C2 |
|
|
|
|
C3 |
|
M |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
q2 |
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Звено 2: |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
l2 |
|
В |
|
|
|
l3 |
|
|
|
|
|
|
|
|
|
|
|
|
T2 1 |
m2 vc22 |
|
T J2Ω(2)2 , |
|||||||||||
|
|
Q2 |
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
F |
|
|
|
Ω(2)2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
Q1 |
|
|
|
|
|
|
q1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
vс2 – скорость центра масс второго |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
звена, |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m2 – его масса, |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J2 – тензор инерции, |
|
|
|
|
|||||||||
x |
|
Ω(2)2 – вектор-столбец угловой ско- |
|
Рис. 6.3 |
|||
рости в проекции на оси С2x2y2z2. |
|||
|
|
175
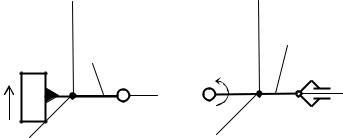
a) |
х2 |
б) y3 |
|
2 |
|
Q3 |
|
|
|
q3 |
||
|
|
|
||
q2 |
А |
|
z2 |
|
В |
В |
|||
Q2 |
C2 |
|||
y2 |
|
z3 |
||
|
|
|
3 |
|
M |
C3 |
x3 |
Рис. 6.4
Найдем vс2 и Ω(2)2 |
: |
|
|
||||
2 |
|
2 2 |
|
2 |
, |
|
|
vс2 |
2q1 |
|
q2 |
|
|||
|
(2) |
|
q |
|
|||
|
|
2 x |
|
|
|||
|
|
|
|
|
|
|
|
(2) |
|
(2) |
|
|
1 |
|
|
Ω2 |
2 y |
|
|
0 |
. |
||
|
|
(2) |
|
|
0 |
|
|
|
|
2 z |
|
|
|
||
|
|
|
|
||||
Подставим найденные значенияв выражение для кинетической энергии Т2:
T2 12 m2 22q12 m2q22 J2 xq12 12 J2 z1 q12 m2q22 ,
где J2 z1 m2 22 J2 x . Кинетическая энергия третьего звена Т3:
T3 12 m3vс23 Ω3(3)T J3Ω3(3) .
Найдем скорость центра масс третьего звена vс3.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 sin q1 cos q3 |
asin q1 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
r(0) |
|
|
3 |
cos q |
cos q |
|
a cos q |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
|
|
|
|
1 |
, |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
c3 |
|
|
|
|
|
3 sin q3 |
q2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
cos q cos q |
|
|
|
|
|
|
|
sin q sin q |
|
|
|
|
v |
(0) |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
a cos q )q |
|
|
q |
|
|
c3x |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
1 |
|
|
3 |
|
1 |
|
1 |
|
|
3 |
|
1 |
3 |
|
3 |
|
|
(0) |
|
|||
|
|
|
|
|
|
|
|
( 3 sin q1 cos q3 |
|
|
|
3 cos q1 sin q3 |
|
|
v |
|
|
|
|||||||||||||||||
|
|
(0) |
(0) |
|
|
asin q1)q1 |
q3 |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c3 y |
|
|
|||||||
|
|
|
vc3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(0) |
, |
|
||
|
rc3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 cos q3 q3 q2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c3z |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
vc3 |
2 |
|
|
(0) |
2 |
|
|
(0) |
|
2 |
|
(0) |
|
2 |
3 cos q3 |
a |
2 |
2 |
2 2 |
|
|
|
|
|
|
|
|
2 |
|||||||
|
vc3x |
|
vc3 y |
|
vc3z |
|
|
q1 3q3 |
2 3 cos q3 q2q3 |
q2 |
|||||||||||||||||||||||||
176

Положим, что звено 3 представляет собой тонкий однородный стержень, а3 b 2 . Тогда компоненты тензора инерции J3, построенного в осях С3x3y3z3 :
2 . Тогда компоненты тензора инерции J3, построенного в осях С3x3y3z3 :
J3x = 0; J3y = J3z = m3b2  12 ; J3xy = J3xz = J3yz = 0. Угловая скорость Ω3(3) :
12 ; J3xy = J3xz = J3yz = 0. Угловая скорость Ω3(3) :
|
|
|
|
|
|
|
|
|
|
|
q sin q |
|
|
|
(3) |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3) |
|
1 |
3 |
|
|
|
|
(3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ω3 |
q1 cos q3 |
|
|
3 y |
. |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q3 |
|
|
3z |
|
|
|
|
|
|
|
|
|
|||
Отсюда получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
T3 |
|
1 |
m3 |
b |
cos q3 |
2 |
2 |
|
b2 |
2 |
|
|
|
|
|
2 |
|
b2 |
2 |
cos |
2 |
q3 |
2 |
|
||
2 |
|
2 |
a |
q1 |
4 |
q3 bcos q3 |
q2 q3 |
q2 |
12 |
q1 |
|
q3 |
. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полная кинетическая энергия механизма составит:
T T1 T2 T3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
b |
|
2 |
|
m b2 |
2 |
|
2 |
|
|||||
|
|
J1z |
J2 z m3 |
|
cos q3 a |
|
3 |
|
cos q3 |
q1 |
|
||||||
|
2 1 |
1 |
|
2 |
|
|
|
12 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
m3b2 |
2 |
|
|
|
|
|
|
|
|
|
||
2 |
m2 |
m3 q2 |
|
3 |
|
q3 m3bcos q3 |
q2q3 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Найдем обобщенные силы сопротивления. |
|
|
|
|
|
|
|
|
|
||||||||
Q G zC 2 G |
zC3 F xM |
F |
|
yM |
F |
|
zM |
. |
|||||||||
|
|
|
|||||||||||||||
|
Cs |
2 qs |
|
3 qs |
x qs |
|
y qs |
|
z qs |
|
|||||||
Здесь учтено, что центр масс звена 1 не изменяет своего положения. Из ки-
нематического анализа несложно получить выражения для zс2 |
qS |
и zс3 |
qS : |
||||||||||
zc2 0 , |
zc2 1, |
zс2 |
0 , zс3 |
0 , |
zс3 1, zс3 |
b cos q . |
|
|
|
||||
q1 |
q2 |
q3 |
|
q1 |
|
q2 |
q3 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
||||||||
Функция положения точки М: |
|
|
|
|
|
|
|
||||||
|
|
|
|
xM(0) |
|
bsin q |
cos q asin q |
|
|
|
|
||
|
|
|
|
|
|
|
1 |
3 |
1 |
|
|
|
|
|
|
r |
|
yM(0) |
|
bcos q1 cos q3 a cos q1 |
. |
|
|
|
|||
|
|
M |
|
(0) |
|
|
(b c)sin q3 q2 |
|
|
|
|
||
|
|
|
|
zM |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||
177
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xM |
bcos q |
cos q a cos q , |
yM |
bsin q |
cos q |
asin q , zM |
0 , |
||||||||
q |
3 |
|
1 |
|
|
1 |
q |
|
|
1 |
|
3 |
1 |
q |
|
1 |
|
|
|
xM |
|
1 |
yM |
|
|
zM |
|
|
1 |
|
|
|
|
|
|
0 ; |
0 ; |
1, |
|
|
|||||||
|
|
|
|
q |
2 |
|
|
q |
|
|
q |
|
|
|
|
xM |
bsin q sin q , yM |
|
|
|
2 |
|
zM |
2 |
|
|
|
|
|||
bcos q sin q |
, |
bcos q . |
|
|
|||||||||||
q |
1 |
3 |
q |
|
|
|
1 |
3 |
q |
|
|
3 |
|
|
|
3 |
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
Теперь несложно найти обобщенные силы сопротивления:
QC1 Fx cos q1 Fy sin q1 bcos q3 a ,
QC 2 G2 G3 Fz ,
QC3 G3 b2 cos q3 Fxbsin q1 sin q3 Fybcos q1 sin q3 Fzbcos q3 .
Подставляя найденные значения в уравнения Лагранжа, получим три уравнения движения:
|
|
|
|
|
|
|
b |
|
|
|
|
2 |
|
m b2 |
|
2 |
|
|
|||
J1z |
J2 z |
m3 cos q3 |
a |
|
|
|
3 |
cos |
|
q3 q1 |
|||||||||||
|
1 |
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
bcos q3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
m3bsin q3 |
3 |
a q1q3 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q1 |
Fx cos q1 Fy sin q1 bcos q3 a , |
|
|
|
|
||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
2 |
sin q3 ) Q2 |
G2 |
G3 Fz , |
|||||||
m2 m3 q2 |
2 |
m3b(cos q3 q3 |
q3 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m3b2 |
1 |
m3bcos q3 |
q2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
q3 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
3 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
b2 |
cos q3 sin q3 |
b |
|
|
|
|
|
2 |
|
|
|||||||
|
|
m3 |
3 |
2 |
am3 sin q3 q1 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Q3 G3 b2 cos q3 Fxbsin q1 sin q3 Fybcos q1 sin q3 Fzbcos q3.
Из приведенных уравнений видно взаимовлияние приводов. Например, двигатель 2 «чувствует», как работает двигатель, приводящий в движение звено 3 (движущий момент Q2 зависит от q3 и от q3 ).
178
