Добавил:

Xer1t Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский политехнический университет Петра Великого (бывш. СПбГПУ)

Предмет:

Теория механизмов и машин

Файл:

ЭКЗ / tmm_chapter2

.pdf

Скачиваний:

Добавлен:

26.11.2019

Размер:

330.63 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

ГЛАВА 2. ГЕОМЕТРИЯ И КИНЕМАТИКА МЕХАНИЗМОВ

2.1. Геометрический анализ механизмов

Зависимость выходных параметров от входных обобщенных координат механизма называется функцией положения механизма.

Для механизма, показанного на рис. 2.1:

	y	2	B				xK Пx (q1 );		(2.1)
А	K		B				yK Пy (q1 ).		(2.1)
А	2			3			yK Пy (q1 ).
	2
					Определение		функций	положения
1	q1		3	x	Определение		функций	положения
	O		3	x	механизма составляет прямую				задачу
	I		C		геометрического анализа.
	I			II	Рассмотрим		последовательность
	Рис. 2.1			II	составления	функции		положения
	Рис. 2.1				хК(t)=ПХК[q1(t)], yK(t)=ПYК[q1(t)]
					хК(t)=ПХК[q1(t)], yK(t)=ПYК[q1(t)]
1.Проводится структурный анализ механизма:

Однозвенная одноподвижная СГ I (кривошип 1 и вращательную пару О),

Диада ВВВ, содержащую звенья 2 и 3 и три вращательные пары А, В и С.

	y	2	B
А	K		B
А	2			3
	2

1	q1		3	x
	O		3	x
	O		C
	I		C
	I			II
	Рис. 2.1			II
	Рис. 2.1

2.В каждой структурной группе

вводятся входные и выходные коор-

динаты.

3.Путем размыкания некоторых кинематических пар структурные группы приводят к открытым кинематическим цепям типа «дерево».

4.Вводятся групповые координаты, определяющие, вместе с входными, положение звеньев «дерева». Число групповых координат должно быть равно числу разомкнутых связей (на рис. 2.1 это углы 2 и 3).

5.Составляются условия замыкания ранее разомкнутых связей и функции

положения. На основе этих условий получаются групповые уравнения, связывающие входные, выходные и групповые координаты структурной группы.

	y	2	B
А	K		B
А	2			3
	2

1	q1		3	x
	O		3	x
	O		C
	I		C
	I			II
	Рис. 2.1			II
	Рис. 2.1

Функции положения для группы I:

				xA l1 cos q1			,		(2.2)
				уA l1 sin q1.					(2.2)
				уA l1 sin q1.
Групповые уравнения для группы II:
xA l2 cos 2						xC l3 cos 3 ;			(2.3)
y	A	l	2	sin	2	y	l	sin .	(2.3)
	A		2		2	C	3	3

Уравнения получены из условия замыкания связей в шарнире В (неизвестны групповые координаты 2 и 3)

Функции положения точки К группы II:

xK xA lAK cos 2	;	(2.3 )
yK yA lAK sin 2 .		(2.3 )
yK yA lAK sin 2 .
ФП для механизма с несколькими (W) степенями подвижности:
xs Пs (q1,..., qW ), s = 1, …, m,		(2.4)

где m – число выходных координат.

Составление функций положения на примере плоской платформы (рис. 2.2).

1. Структурный анализ механизма.									Три структурные группы:
		y							Три структурные группы:
		y	3	M	3	C	4	III	однозвенные одноподвижные I и II,
2		B	3	M					трехзвенную одноподвижную III.
		B							трехзвенную одноподвижную III.
					q3		4	II	2. Введем входные и выходные коор-
А			2			D	4	II	2. Введем входные и выходные коор-
									динаты.
							5		динаты.
1			q1			E	5	x	Группа I: вход хО, уО, q1,
1	O		q1			E	q2	x	выход хА, уА;
	I								Группа II: вход хЕ, уЕ, q2,
	I								выход xD, yD;
			Рис. 2.2						выход xD, yD;
			Рис. 2.2						Группа III: вход хА, уА, хD, yD, q3,

выход хМ, уМ, 3.

			y	3		M		3		C	4
	2		B							C	4
	2						q3				4
А				2					D		4

											5
1				q1					E		5
1		O		q1					E		q2
		O
		I
					Рис. 2.2
	xA l1 cos q1,				,	xD xE l5 cos q2 ;
	у	A	l sin q .			y	D	y	E	l	sin q ;
		A	1	1			D		E	5	2

	3.Произведем размыкание группы
III III в шарнире C
II	4.Введем групповые координаты:
II	2, 3, и 4.
	5.Запишем условия замыкания: xC3
x	= xC4, уC3 = yC4.
	Составим групповые уравнения:

Группа I,II:

Группа III:

xA l2 cos 2	l3 cos 3	xD l4 cos 4	;	(2.5)
yA l2 sin 2	l3 sin 3	yD l4 sin 4 .

Дополнительное уравнение для углов:

3 + q3 = 4.

(2.6)

Обратная задача геометрического анализа: определение обобщенных входных координат в зависимости от выходных, т.е. отыскание функций:

qк = Фк (х1, … , хm), к = 1, … , W.

(2.7)

m= W (число выходных координат равно числу степеней подвижности):

II		y	3 M	3
2		B	3 M	3
		B
				q3
А			2	q3
А			2
1	O		q1
	O

Рис. 2.3

C 4

E q2

задача может иметь одно или неIII сколько решений;

			m> W:
		задача в общем случае не имеет
5		решения;	m< W:
5	x

		задача имеет бесконечное число ре-

шений (некоторое число координат (а именно W – m) можно задать произвольно).

Пример трехподвижной платформы.

Дано: хМ, уМ, 3.

II		y	3 M	3	C	I		III	Определить: q1, q2, q3.
		B				4		III
2		B				4
2				q3		4
А		2			D	4			Структурный анализ инверсного ме-
А		2			D				Структурный анализ инверсного ме-
1		q1			E	q2	5	x	ханизма.
1	O	q1			E	q2	5	x	Три структурные группы:
	O								однозвенная трехподвижная I ,
									однозвенная трехподвижная I ,
			Рис. 2.3						II и III – двухзвенные группы Ас-
									сура типа ВВВ..

Составим уравнения для группы I:

xB xM	lBM cos 3			;
yB yM	lBM sin 3			;	(2.8)
xC xM lMC cos 3				;

yC yM lMC sin 3.
Для группы II :
l1 cos q1 l2 cos 2 xB ;					(2.9)
l1 sin q1 l2 sin 2		yB .

Для группы III:
xE l5 cos q2	l4 cos 4		xC ;		(2.10)
yE l5 sin q2	l4 sin 4		yC .

Дополнительное уравнение для углов:		3 + q3 = 4.

2.2.Решение групповых уравнений

Если групповые уравнения имеют решение, то оно, как правило, является не единственным.

xB xA AB cos 2 ;

yB yA AB sin 2 e.

M = -1

M = 1

Определяем: из второго урав-

нения находим sin 2,

1 sin2 2 ,

находим cos 2

подставляем в первое выраже-

Рис. 2.4

ние и находим xB.

cos 2 М

1 sin2 2

, где M 1 – способ сборки.

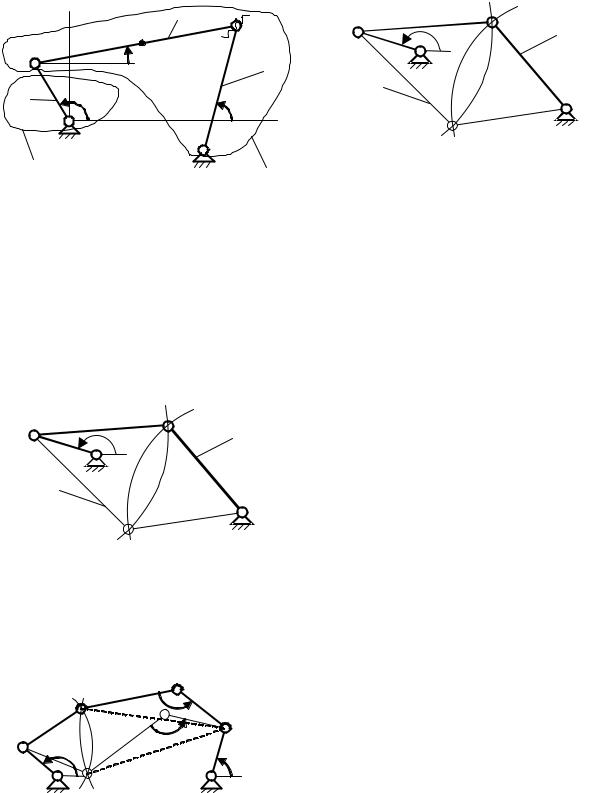
Шарнирный четырехзвенник.
	y	2	B		А		B1
А	K		B			q1	B1	M= -1
А	2			3
	2					O
					1
					1
1	q1		3	x	M=			C
	O		3	x				C
	O		C			B2
	I		C			B2
	I			II		Рис. 2.5
	Рис. 2.1			II		Рис. 2.5
	Рис. 2.1

М= 1 (положение АВ2С ) – обход шарниров в последовательности А,В,С

происходит против часовой стрелки.

М= –1 (положение АВ1С ) – обход шарниров в последовательности А,В,С

происходит по часовой стрелке.

Особое или сингулярное положение (если АВ+ВС=ОА+ОС при

определенном q сборки совпадают).					В механизме, в котором существует
А					В механизме, в котором существует
А			B1	M= -1	особое	положение,		после		его
		q1	B1		прохождения		возможна		перемена
		q1			прохождения		возможна		перемена
		O			способа сборки и, следовательно,
1		O			реализация	побочного			решения
M=				C	групповых уравнений.
				C	групповых уравнений.
		B2			Следует избегать такого				сочетания
		Рис. 2.5			размеров,	при	котором		возможно
		Рис. 2.5			особое положение.
					особое положение.
Трехподвижная платформа.
	B1	C2	C1		Две разные конфигурации груп-
			q3		Две разные конфигурации груп-
А			q3	D	пы:
А		q3		D	пы:
q1		q3	E	q2	АВСD: АВ1С1D и АВ2С2D.
O		B2	E	q2
O		B2

Рис. 2.6

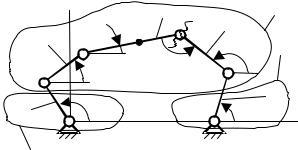
Решение групповых уравнений на ЭВМ

	y	3 M	3				III	Пусть одно решение групповых
	B		3	C	4		III
					4
2					4		II	уравнений механизма уже получе-
А		2	q3	D	4		II	но.
			q3					но.
						5		Координаты, соответствующие
								Координаты, соответствующие
1	O	q1		E	q2		x	этому положению, обозначим зна-
	O							ком (): q1=q1, q2=q2, q3=q3, 2= 2*,
	I							ком (): q1=q1, q2=q2, q3=q3, 2= 2*,
	I							3= 3*.
		Рис. 2.2
Дадим малые приращения входных координат q1, q2, q3.
Получим		новые	значения		входных			координат: q1=q1+ q1, q2=q2+ q2,

q3=q3*+ q3.

Тогда решение 2 и 3 будет единственным, поскольку второе положение механизма, соответствующее тем же приращениям координат q1, q2 и q3, окажется далеким от исходного положения механизма.

Определим малые приращения 2 и 3 из групповых уравнений:

xA l2 cos( 2* 2 ) l3 cos( 3* 3 ) xD l4 cos( 3* 3 q3* q3 ) 0; yA l2 sin( 2* 2 ) l3 sin( 3* 3 ) yD l4 sin( 3* 3 q3* q3 ) 0.

При этом предположим, что приращения хА, уА, хD, уD уже получены решением групповых уравнений групп I и II.

Или в обобщенной форме:
F( ,ξ,q3 ) 0 ,							(2.11)
где F, ,ξ, – векторы-столбцы:
					xA
	F				xD
F	1	;	2		;ξ	.
	F				yA
	2		3

При этом					yD
При этом
F1( ,ξ,q3 ) xA l2 cos 2		l3 cos 3		xD l4 cos( 3 q3 ) ;
F2 ( ,ξ,q3 ) yA l2 sin 2 l3 sin 3			yD l4 sin( 3 q3 ) .				(2.12)

Мы ищем решение векторного уравнения

F( * ,ξ* ξ,q3* q3 ) 0,

(2.13)

Метод Ньютона или метод касательных. В соответствии с этим методом

(k+1)-е приближение для связывается с k-м приближенным соотношением

(k 1)	(k )	F 1	F *	(k )	,ξ* ξ,q3*	q3 , k = 1, 2, ... . (2.14)
			F *		,ξ* ξ,q3*	q3 , k = 1, 2, ... . (2.14)
		k

Доказано, что в достаточно малой окрестности исходного решения *

последовательность (2.14) сходится, причем обеспечивается квадратичная сходимость. Выражение

F	F	*	(k )	,ξ* ξ,q3*	q3 .
		*		,ξ* ξ,q3*	q3 .
k

представляет собой матрицу Якоби для системы (2.11).

Для рассмотренных групповых уравнений

F1( ,ξ,q3 ) xA l2 cos 2 l3 cos 3 xD l4 cos( 3 q3 ) ; F2 ( ,ξ,q3 ) yA l2 sin 2 l3 sin 3 yD l4 sin( 3 q3 ) .

F	l2 sin 2				l3 sin 3 l4 sin( 3				q3 )
	l	2	cos	2	l	cos	l	cos(	q	) .
		2		2	3	3	4	3	3

Определитель этой матрицы (якобиан) определяется выражением

det F l2 l3 sin( 3 2 ) l4 sin( 3 2 q3 ) .

(2.12)

(2.15)

(2.16)

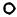
	F
det	/ 2

		Рис. 2.7
Побочное		f
Побочное		Искомое			а)	б)
решение		Искомое			а)	б)
		решение			C		C
		*	А		C		C
		2	А	B	q3	B	q3
		2		B		B
		1
		1			D	А	D
					D	А	D

Рис. 2.8	Рис. 2.9

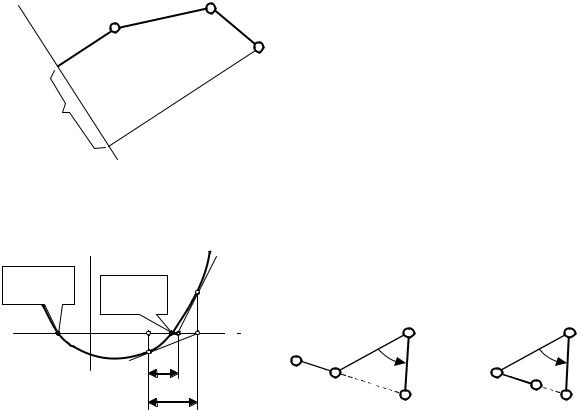
На рис. 2.8 дана условная геометрическая интерпретация метода Ньютона, относящаяся к случаю, когда векторы F и – одномерные.

Для того, чтобы избежать многократного вычисления матрицы F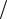 k1 ,

обратной матрице Якоби, можно пользоваться модифицированным методом Ньютона (методом секущих), при котором используется процедура, соответствующая формуле

(k 1)

(k )

F 1

F *

(k )

,ξ* ξ,q3*

q3 ,

k = 1, 2, … . (2.17)

где

,ξ

, q .

Положение механизма, близкое к исходному, не может быть получено описанным выше способом, если определитель матрицы Якоби обращается в ноль. Это – особое (сингулярное) положение группы АВСD.

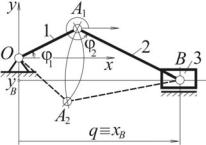
Пример с ползунно-кривошипным механизмом. Вход q xB.

Вмеханизме две структурные группы:

однозвенная одноподвижная (ползун 3)

двухзвенная группа Ассура типа ВВВ

(звенья 1 и 2).

Такой механизм при одном значении q может принимать две различные конфигурации: ОА1В и ОА2В, причем без разборки механизма.

Составим выражения для F:

FF1( ,q) l1 cos 1 l2 cos 2 q ,

F2 ( ,q) l1 sin 1 l2 sin 2 yB

где φ 1 . Матрица Якоби:

F	l1 sin 1		l2 sin 2
	l	cos	l	cos	2	.
	1	1	2		2

Определитель матрицы Якоби (якобиан):

l1l2 sin 1 cos 2 l1l2 cos 1 sin 2 l1l2 sin( 2 1) .

Отсюда видно, что якобиан обращается в 0 тогда, когда все три шарнира находятся на одной прямой (sin( 2 – 1) = 0 – особое положение группы ВВВ).

Найдем обратную матрицу:

																1		cos 2		1		sin 2
F	1			1			l2 cos 2			l2 sin 2		1				l1		cos 2		l1		sin 2
F				1			l2 cos 2			l2 sin 2		1				l1				l1
φ								l	cos	l	sin						1				1
φ			l l	sin(		)		l	cos	l	sin		sin(		)		1				1
		1 2			2	1		1	1	1	1			2	1				cos				sin
		1 2			2	1		1	1	1	1			2	1				cos				sin
																	l2		1		l2		1
																	l2				l2

Тогда

1 (k 1)2

1 (k )2

			1				k
	1		l			cos 2
	1			1
sin( k		k )		1			cos	k
2		1
2		1
					l2		1
					l2

sin 2

l1 cos 1

l2 cos 2

sin k

sin

где 1k 1* 1k , k2 2* k2 , k = 0,1,2, … . В особом положении (т.е. при sin( 2 – 1) = 0) данный метод не работает.

2.2. Кинематический анализ механизмов

Задачей кинематического анализа является определение скоростей и уско-

рений точек механизма, угловых скоро-

стей и угловых ускорений его звеньев.

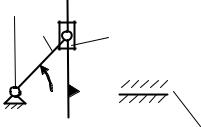
Синусный механизм.

Функция положения точки B:

xB 1 cos q x (q) .

Рис. 2.10

Дифференцируя ее по времени, по-

лучим скорость точки В:

dxB

x q

1 sin q q

x q

q .

Продифференцировав по времени

xB , получим ускорение точки В:

d 2 xB

1 cos q (q)

1 sin q q

dt2

2 x

x (q)

d 2q

dt2

(q) q

(q) q.

x – аналог скорости или первая геометрическая передаточная функция;

x – аналог ускорения или вторая геометрическая передаточная функция; q – обобщенная скорость; q – обобщенное ускорение.

Для одноподвижного механизма (W = 1) функция положения:
	xМ = Пх(q),.				(2.18)
Дифференцируя (2.18) по времени, получим:
	dxM	x	dq		(2.19)
xM	dt	q	dt	x q ,

Для определения ускорения точки М продифференцируем выражение (2.19) по времени:

d 2 xM

2 x

dq 2

d 2q

(2.20)

dt2

(q)

x q ,

При q = const, q = 0

(q)

1 / 21 2 > Следующая >>>

Соседние файлы в папке ЭКЗ

#
26.11.2019317.27 Кб16tmm_chapter1.pdf
#
26.11.2019421.16 Кб15tmm_chapter10.pdf
#
26.11.2019330.63 Кб13tmm_chapter2.pdf
#
26.11.2019236.12 Кб12tmm_chapter3.pdf
#
26.11.2019578.58 Кб14tmm_chapter4.pdf
#
26.11.2019368.98 Кб15tmm_chapter5.pdf
#
26.11.2019544.88 Кб12tmm_chapter6.pdf
#
26.11.2019621.4 Кб13tmm_chapter7.pdf