4.6 Задача про вимушені коливання струни

Нехай маємо однорідну струну довжиною , закріплену на обох кінцях . На струну весь час діє збудження . Необхідно знайти розв’язок неоднорідного рівняння, що задовольняє умовам

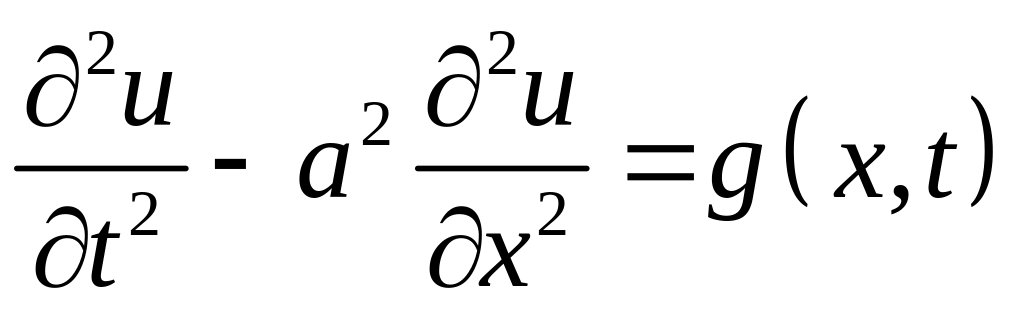(4.51)

; (4.52)

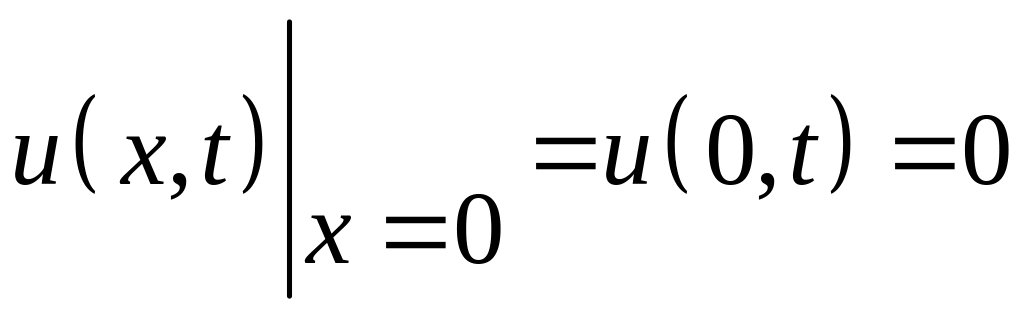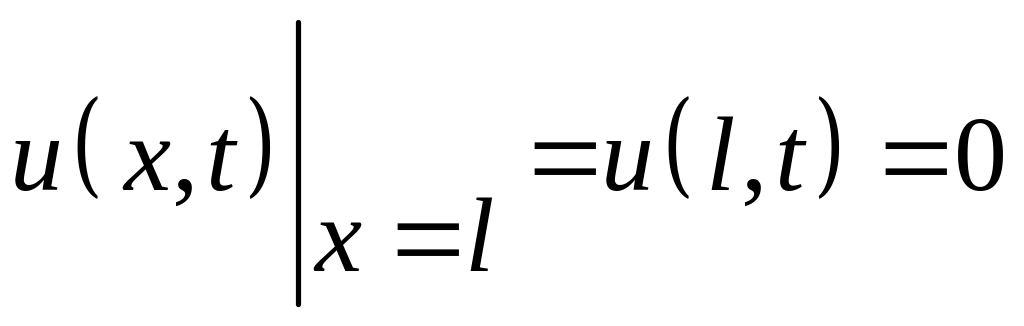; (4.53)

Для такого рівняння поділ змінних неможливий. Тому шукаємо розв’язок задачі (4.51)-(4.53) у вигляді суми функцій

, (4.54)

де функція – розв’язок однорідного рівняння

; ,

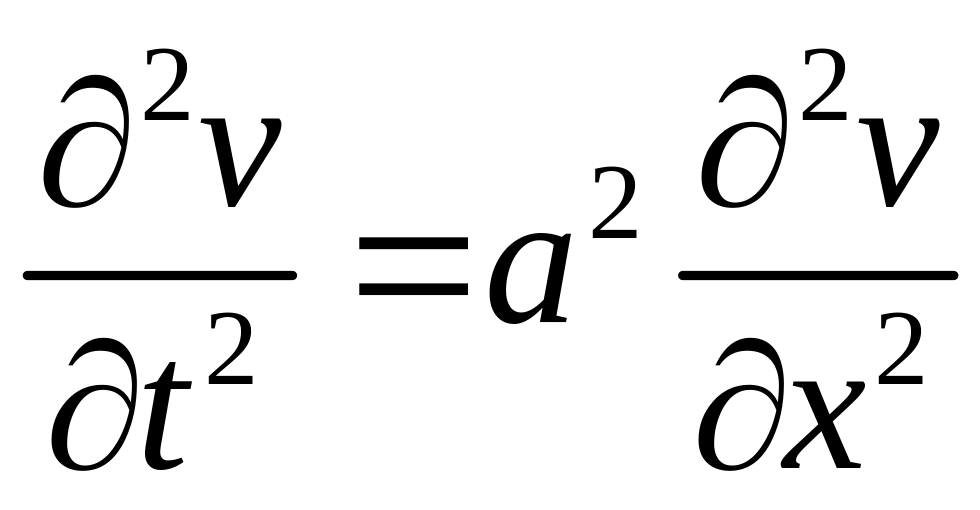що задовольняє умовам (4.52), (4.53), а функція є розв’язок неоднорідного рівняння (4.51), що задовольняє однорідним умовам

, (4.55)

(4.56)

(4.57)

Безпосередня перевірка показує, що складена функція (4) є розв’язком задачі (4.51)-(4.53) .

Розв’язок задачі (4.55)-(4.57) знайдено методом поділу змінних Фур’є у вигляді (4. 49).

Шукаємо розв’язок неоднорідної задачі з однорідними умовами у вигляді ряду за власними функціями задачі (4. 36).

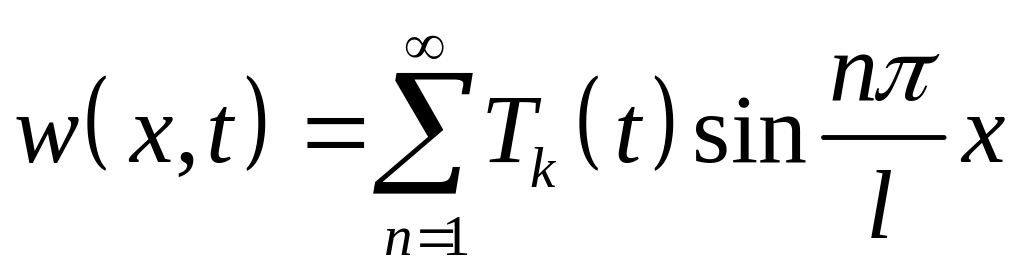(4.58)

Підбираємо функцію так, щоб ряд (4.58) задовольнив рівнянню (4.55) та однорідним початковим умовам (4.56)

(4.59)

Диференціюючи (4.58) за змінною та підставляючи в рівняння (4.55), будемо мати

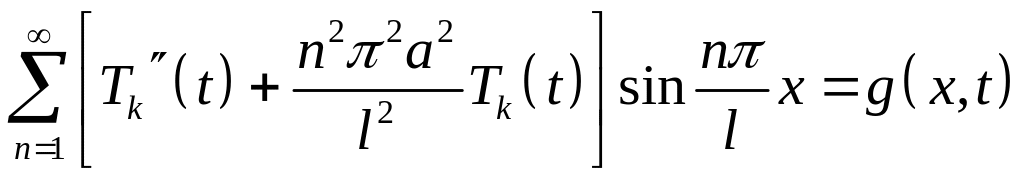(4.60)

Зафіксувавши , розкладемо функцію у ряд за власними функціями (4. 36) –однорідної задачі (в ряд синусів)

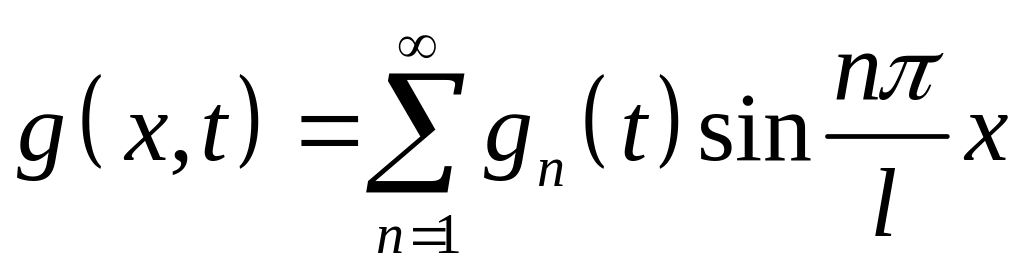, (4.61)

де

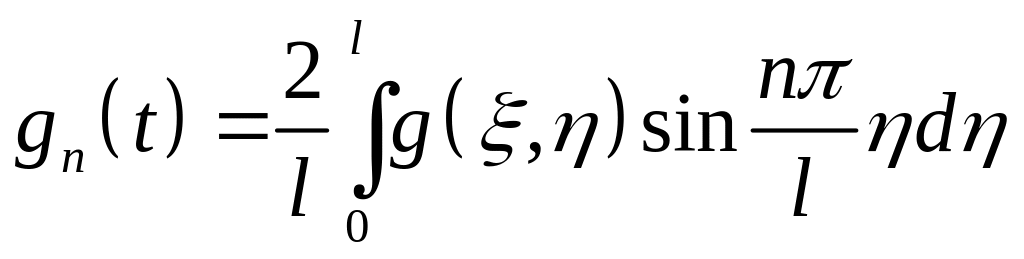
Підставляючи (4.61) y (4.60), будемо мати

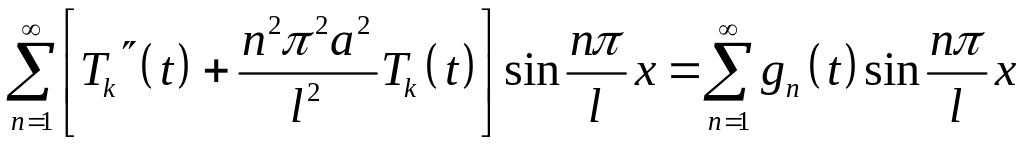(4.62)

Остання рівність можлива, коли рівні між собою вирази під знаком суми в (4.62). Приходимо до звичайного диференціального рівняння з однорідними умовами Коші

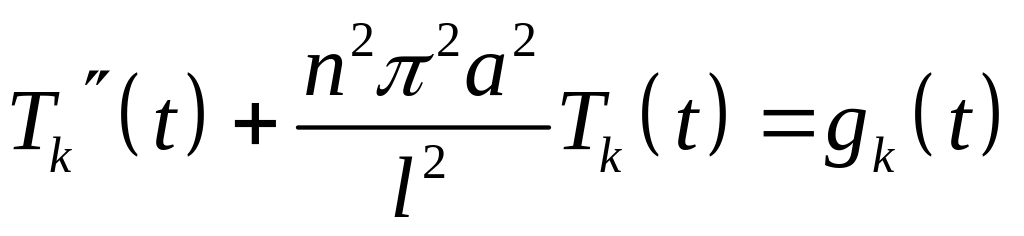
Ця задача є задачею Коші для звичайного диференціального рівняння другого порядку

(4.63)

де , .

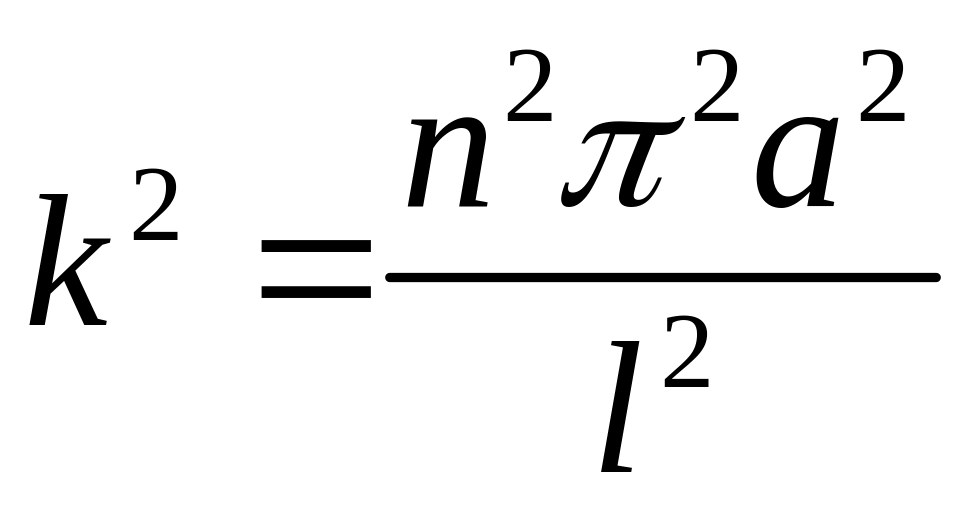Складемо характеристичне рівняння

, де – частинний розв’язок неоднорідного рівняння (4.63). Підставивши розв’язок задачі (4.63) у (4.58) отримаємо розв’язок задачі для неоднорідного рівняння з однорідними умовами (4.55)–(4.57).

4.7 Неоднорідна перша крайова задача

Якщо кінці струни рухаються за певним законом, то для такої задачі формулюються неоднорідні граничні умови . У такому випадку маємо задачу

; (4.64)

; (4.65)

. (4.66)

Така задача ще називається мішаною. Шукаємо її розв’язок у вигляді суми двох функцій

, (4.67)

де – нова шукана функція, а – довільна функція, що задовольняє неоднорідним крайовим умовам.

Нехай , де – двічі диференційовані функції.

Підставляємо їх значення до крайових умов. Тоді маємо

,

.

Отже,

. (4.69)

Підставляючи (4.67) до (4.64), приходимо до задачі

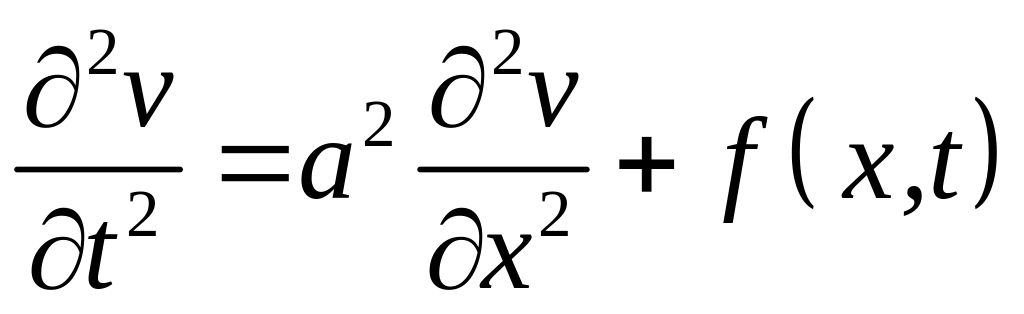, (4.70)

; (4.71)

; , (4.72)

де

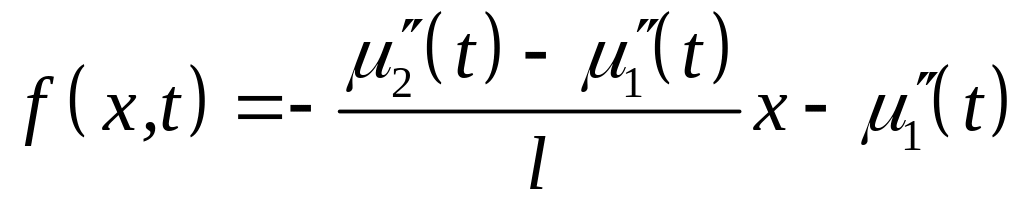
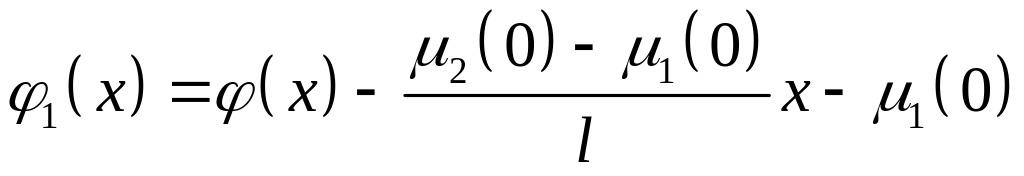(4.73)

Знайшовши розв’язок задачі (4.70)–(4.72), яка є задачею (4.51)–(4.53) у вигляді (4.58) та додавши до неї (4.69), ми отримаємо розв’язок неоднорідної крайової задачі (4.64)–(4.66) для хвильового рівняння.

Зауваження. Якщо у задачі (4.64)–(4.66) граничні умови другого роду, а саме , , то функцію шукаємо у вигляді . Тоді, після підстановки крайових умов, функція має вигляд

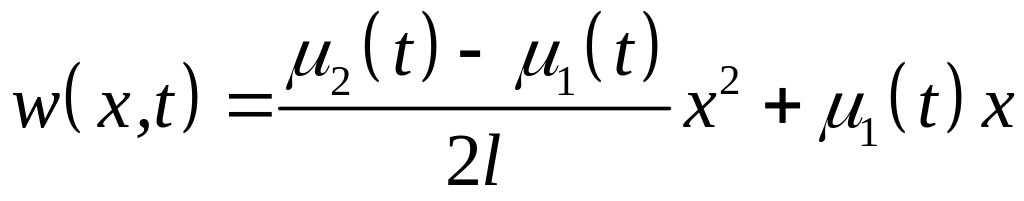
При цьому задача (4.45)-(4.47) повинна задовольняти однорідним крайовим умовам, що мають вигляд ; .

У такій постановці власні значення однорідної задачі (4.70)–(4.72) мають вигляд , а власні функції .

Приклад 4.3

Розв’язати задачу

;

, ;

, .

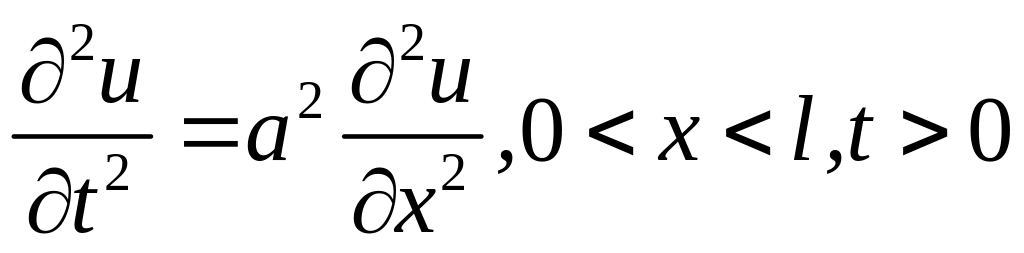Шукаємо розв’язок у вигляді (4.67)

.

Згідно з (4.68) функція має вигляд

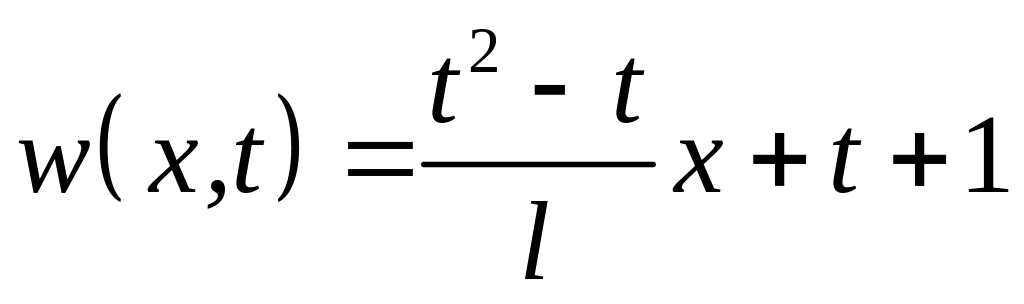. (4.74)

Функції та відповідно до (4.73)

.

Маємо задачу з однорідними граничними умовами

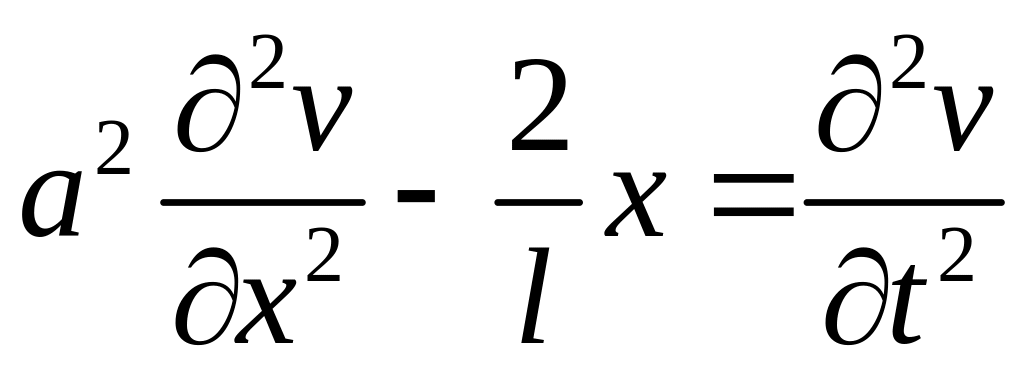, , (4.75)

, , (4.76)

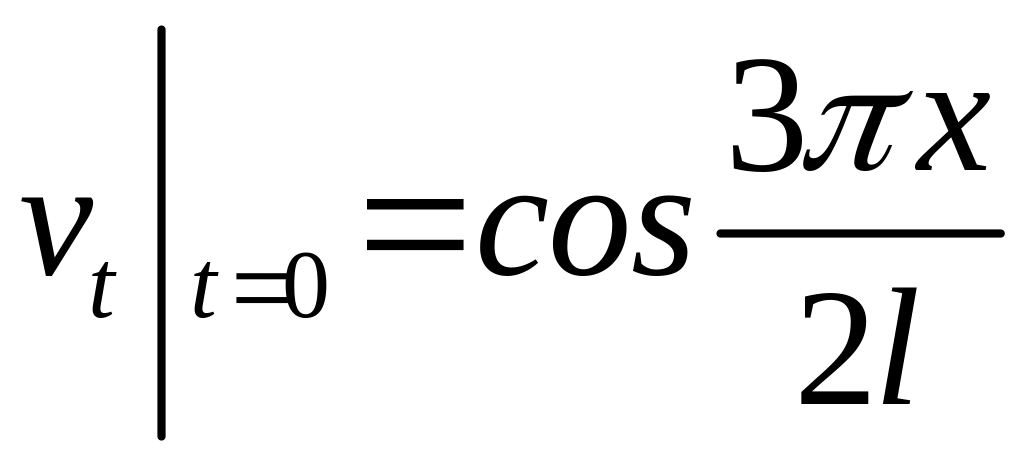, . (4.77)

Розв’язок задачі (4.75)-(4.77) шукаємо у вигляді

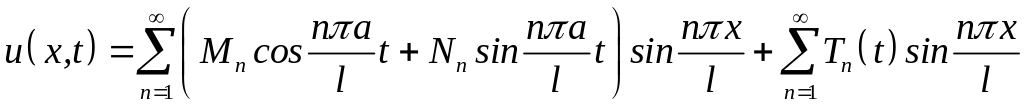, (4.78)

де

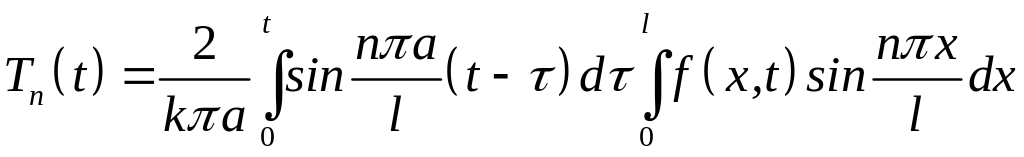(4.79)

Отже, щоб розв’язати першу крайову задачу з неоднорідними граничними умовами, необхідно знайти розв’язок двох задач одна з яких є першою крайовою задачею з однорідними граничними умовами (4.69)–(4.71), а друга повинна задовольняти неоднорідним крайовим умовам (4.65).