3 Середня (стандартна) та гранична помилки вибірки

Оскільки одній генеральній сукупності можуть відповідати різні вибірки, то помилка репрезентативності є випадковою величиною. У зв’язку з цим для оцінки репрезентативності вибірки використовують середню помилку репрезентативності, яку позначають через і називають середньою (стандартною) помилкою вибірки.

Середня помилка вибірки для середньої величини ( ) – це середнє квадратичне відхилення всіх можливих значень вибіркової середньої від генеральної середньої (математичного сподівання) .

Середня помилка вибірки для частки ( ) – це середнє квадратичне відхилення всіх можливих значень частки одиниць, що володіють досліджуваною ознакою, у вибірковій сукупності ( ) від частки одиниць, що володіють цією ж ознакою, у генеральній сукупності ( ).

На середню помилку впливають:

1. показники варіації досліджуваної ознаки: величина помилки зростає із зростанням дисперсії;

2. обсяг вибірки: величина помилки спадає із зростанням об’єму вибірки;

3. методи формування вибірки: при безповторному відборі величина помилки менша, ніж при повторному відборі.

Встановлені у математичній статистиці формули для визначення середньої (стандартної) помилки вибірки для різних методів відбору уточнені в таблиці 1.

Таблиця 1

Середня помилка вибірки для різних типів вибірки

Тип вибірки	Характе-ристики сукупності	Безповторна вибірка	Повторна вибірка
Проста випад-кова і меха-нічна	Середня величина
	Частка
Типова (про-порцій-ний від-бір)	Середня величина
	Частка
Серійна (серії рівно-великі)	Середня величина
	Частка

У таблиці 1 прийняті позначення:

– середня помилка вибірки для середньої;

– середня помилка вибірки для частки;

– вибіркова дисперсія (дисперсія ознаки у вибірковій сукупності);

– обсяг вибірки;

– обсяг генеральної сукупності;

– частка одиниць, що володіють досліджуваною ознакою, у вибірковій сукупності;

– частка одиниць, що не володіють досліджуваною ознакою, у вибірковій сукупності;

– середня групова вибіркова дисперсія середньої (середня з групових), тобто

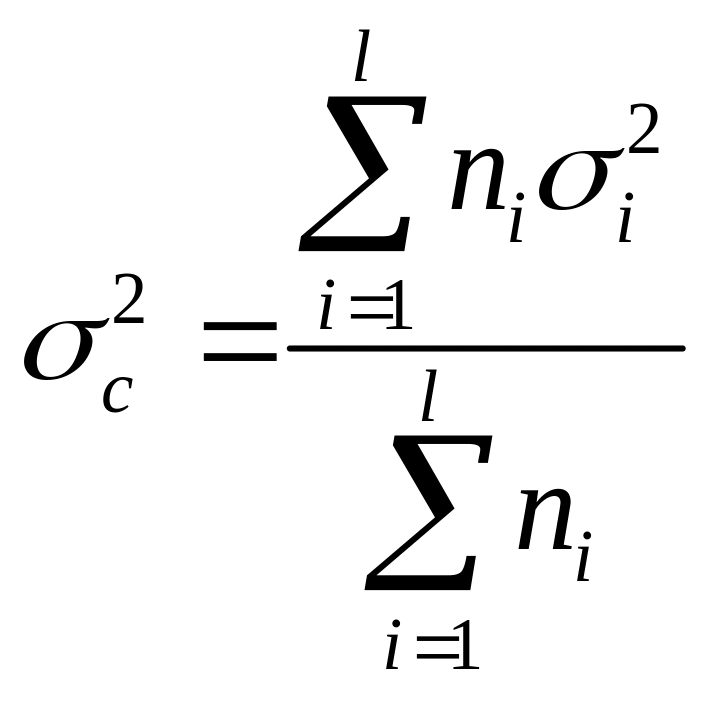, (1)

де – кількість груп, – обсяг -тої групи, а – дисперсія -тої групи;

– середня групова вибіркова дисперсія для частки (середня з групових), тобто

, (2)

де _– частка одиниць сукупності, що володіють досліджуваною ознакою, в -тій типовій групі;

– число рівновеликих серій у генеральній сукупності;

– число рівновеликих серій у вибірковій сукупності;

– міжсерійна вибіркова дисперсія середньої, тобто

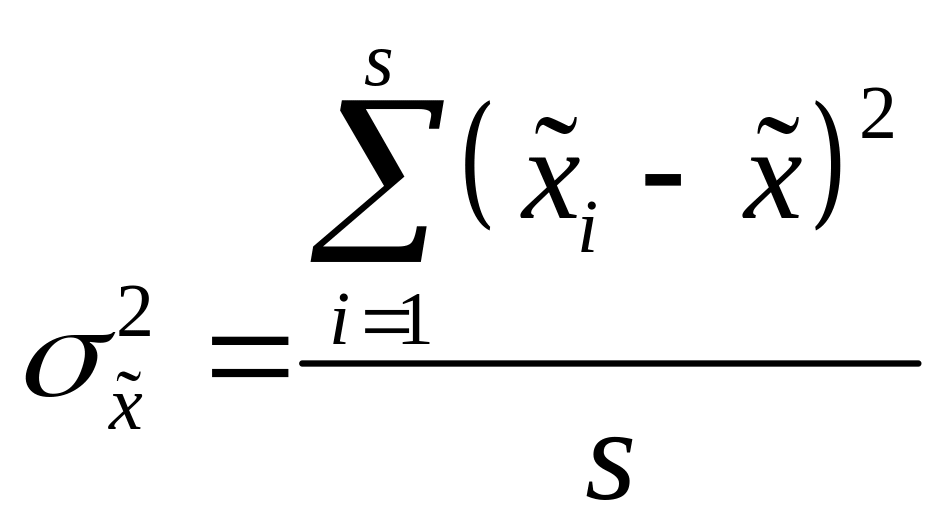, (3)

де – середнє значення ознаки в -тій серії,

– загальна середня у вибірковій сукупності;

– міжсерійна вибіркова дисперсія для частки, тобто

, (4)

де – частка одиниць, що володіють досліджуваною ознакою в -й серії;

– середня вибіркова частка одиниць, що володіють досліджуваною ознакою (при рівновеликих серіях).

Знайшовши дисперсії (1)-(4), відповідні середні помилки розраховують за формулами, вказаними у таблиці 1.

Крім середньої, використовується також гранична помилка вибірки.

Гранична помилка вибірки ( ) – це відхилення вибіркової характеристики від генеральної.

Формули для обчислення граничної помилки вибірки такі:

, , (5)

де – коефіцієнт довіри (рівень значущості) при заданому значенні ймовірності .

Ймовірність появи відповідної помилки вибірки знаходиться згідно з теоремами теорії ймовірності – теоремами П. Л. Чебишева та А. М. Ляпунова.

Теорема П. Л. Чебишева стверджує, що при достатньо великому обсязі вибірки і обмеженій дисперсії генеральної сукупності ймовірність того, що різниця між вибірковою та генеральною середніми буде як завгодно малою, близька до одиниці:

при .

А. М. Ляпунов довів, що незалежно від характеру розподілу генеральної сукупності при зростанні обсязі вибірки розподіл ймовірностей появи того чи іншого значення вибіркової середньої наближається до нормального розподілу (центральна гранична теорема).

З цієї теореми випливає, що розподіл ймовірностей відхилень вибіркової середньої від генеральної середньої, тобто ймовірність появи заданої граничної помилки також підпорядковується нормальному закону розподілу та може бути знайдена як функція від за допомогою інтеграла Лапласа:

,

де − нормоване відхилення вибіркової середньої від генеральної середньої. Функція табульована (додаток А), тому при заданому легко знайти і навпаки.

Частіше всього на практиці використовують такі значення:

, , , .

Використовуючи середні та граничні помилки вибірки, можна вказати довірчі інтервали для генеральних характеристик:

для середньої величини:

для частки:

Чим менший довірчий інтервал, тим точніша оцінка.