Геометрическая интерпретация задачи лп

В курсе математического анализа задача оптимизации решается методами дифференциального исчисления. Почему же задачи ЛП нельзя решать этими методами? Методы дифференциального исчисления позволяют определять только такие экстремальные точки, которые находятся внутри рассматриваемой области, а не на ее границе. В задачах ЛП оптимальное значение линейной формы достигается всегда на гранях многоугольника решений.

Геометрия задачи ЛП.

(1)

Z(x)= -7xl - 5x2 → min х1 = 0

(2)

2x1+ 3x2 <= 19 х2 = 0

(3)

2xl+x2<=13 19 – 2х1 – 3х2 = 0

(4)

3х2<=15 13 – 2х1 – х2 = 0

(5)

3x1 >= 0, х2>=0 15 – 3х2 = 0

(6)

18 – 3х1 = 0

Это уравнение определяет на плоскости некоторую прямую. Она и является геометрическим местом точек, в которых z(x) принимает данное же значение «с». Меняя «с», получаем различные прямые, параллельные между собой -7x1 - 5x2 = с - каждая прямая семейства. При переходе от одной прямой к другой значение линий уровня (линий равных значений) линейной формы z(x) изменяется (см. рис.2.1).

Соответствующие неравенства изображены стрелками, направленными в сторону допустимых решений xj.

2x1 + 3x2 = 19;

2xl + x2 = 13;

xl = 19 - 3x2/2;

19 - 3х2 + х2 = 13;

6 = 2x2x2 = 3;

х1 = 5.

Р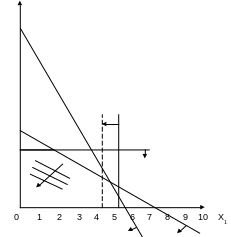 ис. 2.1. Пример задачи, имеющей решение

Вектор g указывает направление, двигаясь в котором мы переходим от больших значений линейной формы к меньшим. Точка Р0 не соответствует оптимальному решению задачи, т.к. внутри многоугольника решений можно найти точ­ки, отвечающие значениям формы, меньшим чем с. Для этого достаточно перейти в направлении вектора g от прямой с к другой, от параллельной прямой семейства все еще пересекающей многоугольник решений.

Оптимальное решение определится точкой С (5,3), при этом z(x)min = -50.

Известно: коэффициенты при переменных в уравнении прямой – суть проекции — вектор «n», перпендикулярного прямой: n={-7;-5}, направление убывания линейной формы (х) противоположно направлению вектора «n».

Множество является выпуклым, т.к. любой отрезок, соединяющий две произвольным образом выбранные точки данного множества, лежит внутри и проходит вдоль границы А, В, С, D - экстремальные точки. Они не могут принадлежать внутренней части ни одного из отрезков, соединяющих две различные точки рассматриваемого множества.

Геометрическая интерпретация этой задачи ЛП имеет вид:

Н еограниченные оптимальные решения

max{z(x)= -2x₁+6x₂} (1)

-lx₁- x₂<= -2 (2)

- x₁+ x₂<=l (3)

x₁>=0 x₂ >=0 (4)

Рис. 2.2 Пример неограниченного оптимального решения

Для данной задачи не существует экстремальных точек, кроме а и b. Зна­чение целевой функции может быть сделано сколь угодно большим, т.е. для любого заданного значения целевой функции в пространстве решений всегда существует точка, в которой целевая функция принимает еще большее значение. Такая точка лежит на прямой, уравнение которой имеет вид:

-х1 +х2 = 1

Задача, не имеющая решения:

max{z(x)= x₁x₂} (1)

-x₁ + x₂<= -1 (2)

x₁ - x₂<= -l (3)

x₁>=0 x₂ >=0 (4)

Рис. 2.3. Задача, не имеющая решения

Вторая геометрическая интерпретация связана с задачами ЛП, представ­ленными в канонической форме:

max{L(x)=cx} al lx1+al2x2+...+alnxn=bl,

Ax=bx>=0 a21xl+a22x2+...+a2nxn=b2

Введем новые переменные:

И1=а11х1+а12х2+...+а1nхn,

И2=а21х1+а22х2+...+а2nхn, *

И3=с1х1+с2х2+...+сnхn

Эти соотношения позволяют для каждой системы и чисел xl,x2,...,xn од­нозначно определить тройку чисел И1,И2,ИЗ.

Введем в трехмерном пространстве прямоугольную систему координат с началом в точке О и осями ОИ1,ОИ2,ОИ3. В этой системе любому вектору x=(xl,x2,...,xn), однозначно сопоставляется точка с координатами И1,И2,ИЗ, вы­числяемые по формуле (*).

Каждому множеству векторов отвечает некоторое множество точек про­странства.