2. Оценка результатов выборочного наблюдения

2.1. Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли

Средняя ошибка выборки показывает, насколько отклоняется в среднем параметр выборочной совокупности от соответствующего параметра генеральной. Если рассчитать среднюю из ошибок всех возможных выборок определенного вида заданного объема (n), извлеченных из одной и той же генеральной совокупности, то получим их обобщающую характеристику  среднюю ошибку выборки ().

В теории выборочного наблюдения выведены формулы для определения , которые индивидуальны для разных способов отбора (повторного и бесповторного), типов используемых выборок и видов оцениваемых статистических показателей.

Например, если применяется повторная собственно случайная выборка, то  определяется как:

^{ при оценивании среднего значения признака;}

^{ если признак альтернативный, и оценивается доля.}

^{При бесповторном собственно случайном отборе в формулы вносится поправка}

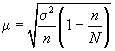^{ для среднего значения признака;}

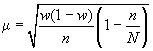^{ для доли.}

Вероятность получения именно такой величины ошибки всегда равна 0,683. На практике же предпочитают получать данные с большей вероятностью, но это приводит к возрастанию величины ошибки выборки.

Предельная ошибка выборки () равна t-кратному числу средних ошибок выборки (в теории выборки принято коэффициент t называть коэффициентом доверия):

  t .

Если ошибку выборки увеличить в два раза (t  2), то получим гораздо большую вероятность того, что она не превысит определенного предела (в нашем случае  двойной средней ошибки)  0,954. Если взять t  3, то доверительная вероятность составит 0,997  практически достоверность.

Уровень предельной ошибки выборки зависит от следующих факторов:

 степени вариации единиц генеральной совокупности;

 объема выборки;

 выбранных схем отбора (бесповторный отбор дает меньшую величину ошибки);

 уровня доверительной вероятности.

Если объем выборки больше 30, то значение t определяется по таблице нормального распределения, если меньше  по таблице распределения Стьюдента (Приложение 1).

Приведем некоторые значения коэффициента доверия из таблицы нормального распределения.

Доверительный интервал для среднего значения признака и для доли в генеральной совокупности устанавливается следующим образом:

Итак, определение границ генеральной средней и доли состоит из следующих этапов:

 нахождение в выборке среднего значения признака (или доли);

 определение  в соответствии с выбранной схемой отбора и вида выборки;

 задание доверительной вероятности Р и определение коэффициента доверия t по соответствующей таблице;

 вычисление предельной ошибки выборки ;

 построение доверительного интервала для средней (или доли).

Ошибки выборки при различных видах отбора

1. Собственно случайная и механическая выборка. Средняя ошибка собственно случайной и механической выборки находятся по формулам, представленным в табл. 11.1.

Таблица 1

Формулы для расчета средней ошибки собственно случайной и механической выборки ()

где ²  дисперсия признака в выборочной совокупности.

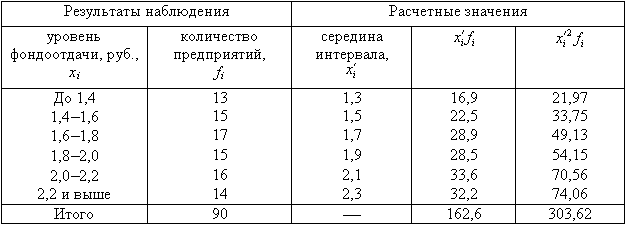
Пример 2. Для изучения уровня фондоотдачи было проведено выборочное обследование 90 предприятий из 225 методом случайной повторной выборки, в результате которого получены данные, представленные в таблице.

В рассматриваемом примере имеем 40%-ную выборку (90 : 225  0,4, или 40%). Определим ее предельную ошибку и границы для среднего значения признака в генеральной совокупности по шагам алгоритма:

1. По результатам выборочного обследования рассчитаем среднее значение и дисперсию в выборочной совокупности:

Выборочная средняя

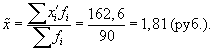
Выборочная дисперсия изучаемого признака

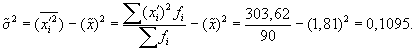
2. Определяем среднюю ошибку повторной случайной выборки

3. Зададим вероятность, на уровне которой будем говорить о величине предельной ошибки выборки. Чаще всего она принимается равной 0,999; 0,997; 0,954.

Для наших данных определим предельную ошибку выборки, например, с вероятностью 0,954. По таблице значений вероятности функции нормального распределения (см. выдержку из нее, приведенную в Приложении 1) находим величину коэффициента доверия t, соответствующего вероятности 0,954. При вероятности 0,954 коэффициент t равен 2.

4. Предельная ошибка выборки с вероятностью 0,954 равна

5. Найдем доверительные границы для среднего значения уровня фондоотдачи в генеральной совокупности

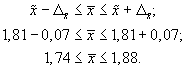
Таким образом, в 954 случаях из 1000 среднее значение фондоотдачи будет не выше 1,88 руб. и не ниже 1,74 руб.

Выше была использована повторная схема случайного отбора. Посмотрим, изменятся ли результаты обследования, если предположить, что отбор осуществлялся по схеме бесповторного отбора. В этом случае расчет средней ошибки проводится по формуле

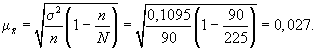
Тогда при вероятности равной 0,954 величина предельной ошибки выборки составит:

Доверительные границы для среднего значения признака при бесповторном случайном отборе будут иметь следующие значения:

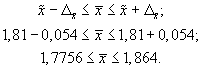
Сравнив результаты двух схем отбора, можно сделать вывод о том, что применение бесповторной случайной выборки дает более точные результаты по сравнению с применением повторного отбора при одной и той же доверительной вероятности. При этом, чем больше объем выборки, тем существеннее сужаются границы значений средней при переходе от одной схемы отбора к другой.

По данным примера определим, в каких границах находится доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., в генеральной совокупности:

1) рассчитаем выборочную долю.

Количество предприятий в выборке с уровнем фондоотдачи, не превышающим значения 2,0 руб., составляет 60 единиц. Тогда

m  60, n  90, w  m/n  60 : 90  0,667;

2) рассчитаем дисперсию доли в выборочной совокупности

_w²  w(1  w)  0,667(1  0,667)  0,222;

3) средняя ошибка выборки при использовании повторной схемы отбора составит

Если предположить, что была использована бесповторная схема отбора, то средняя ошибка выборки с учетом поправки на конечность совокупности составит

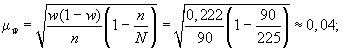
4) зададим доверительную вероятность и определим предельную ошибку выборки.

При значении вероятности Р  0,997 по таблице нормального распределения получаем значение для коэффициента доверия t  3 (см. выдержку из нее, приведенную в Приложении 1):

5) установим границы для генеральной доли с вероятностью 0,997:

Таким образом, с вероятностью 0,997 можно утверждать, что в генеральной совокупности доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., не меньше, чем 54,7%, и не больше 78,7%.

2. Типическая выборка. При типической выборке генеральная совокупность объектов разбита на k групп, тогда

N₁  N₂  …  N_i  …  N_k  N.

Объем извлекаемых из каждой типической группы единиц зависит от принятого способа отбора; их общее количество образует необходимый объем выборки

n₁  n₂  …  n_i  …  n_k  n.

Существуют следующие два способа организации отбора внутри типической группы: пропорциональной объему типических групп и пропорциональной степени колеблемости значений признака у единиц наблюдения в группах. Рассмотрим первый из них, как наиболее часто используемый.

Отбор, пропорциональный объему типических групп, предполагает, что в каждой из них будет отобрано следующее число единиц совокупности:

где n_i  количество извлекаемых единиц для выборки из i-й типической группы;

n  общий объем выборки;

N_i  количество единиц генеральной совокупности, составивших i-ю типическую группу;

N  общее количество единиц генеральной совокупности.

Отбор единиц внутри групп происходит в виде случайной или механической выборки.

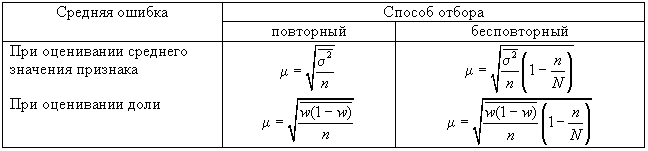
Формулы для оценивания средней ошибки выборки для среднего и доли представлены в табл. 11.2.

Таблица 2

Формулы для расчета средней ошибки выборки () при использовании типического отбора, пропорционального объему типических групп

^{Здесь  средняя из групповых дисперсий типических групп}.

Пример 3. В одном из московских вузов проведено выборочное обследование студентов с целью определения показателя средней посещаемости вузовской библиотеки одним студентом за семестр. Для этого была использована 5%-ная бесповторная типическая выборка, типические группы которой соответствуют номеру курса. При отборе, пропорциональном объему типических групп, получены следующие данные:

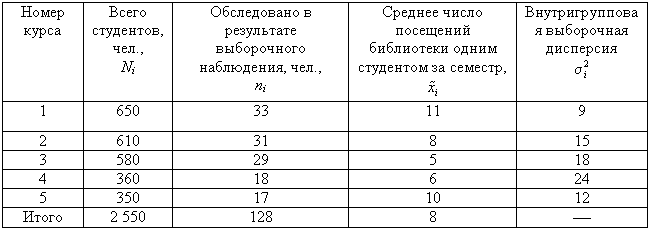
Число студентов, которое необходимо обследовать на каждом курсе, рассчитаем следующим образом:

 общий объем выборочной совокупности:

 количество единиц, отобранных из каждой типической группы:

аналогично для других групп:

п₂  31 (чел.);

п₃  29 (чел.);

п₄  18 (чел.);

п₅  17 (чел.).

Проведем необходимые расчеты.

1. Выборочная средняя, исходя из значений средних типических групп, составит:

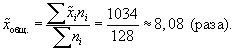
2. Средняя из внутригрупповых дисперсий

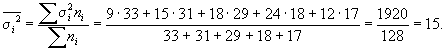
3. Средняя ошибка выборки:

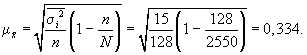
С вероятностью 0,954 находим предельную ошибку выборки:

4. Доверительные границы для среднего значения признака в генеральной совокупности:

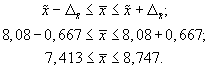
Таким образом, с вероятностью 0,954 можно утверждать, что один студент за семестр посещает вузовскую библиотеку в среднем от семи до девяти раз.

3. Малая выборка. В связи с небольшим объемом выборочной совокупности те формулы для определения ошибок выборки, которые использовались нами ранее при «больших» выборках, становятся неподходящими и требуют корректировки.

Среднюю ошибку малой выборки определяют по формуле

Предельная ошибка малой выборки:

Распределение значений выборочных средних всегда имеет нормальный закон распределения (или приближается к нему) при п  100, независимо от характера распределения генеральной совокупности. Однако в случае малых выборок действует иной закон распределения  распределение Стьюдента. В этом случае коэффициент доверия находится по таблице t-распределения Стьюдента в зависимости от величины доверительной вероятности Р и объема выборки п. В Приложении 1 приводится фрагмент таблицы t-распределения Стьюдента, представленной в виде зависимости доверительной вероятности от объема выборки и коэффициента доверия t.

Пример 4. Предположим, что выборочное обследование восьми студентов академии показало, что на подготовку к контрольной работе по статистике они затратили следующее количество часов: 8,5; 8,0; 7,8; 9,0; 7,2; 6,2; 8,4; 6,6.

Оценим выборочные средние затраты времени и построим доверительный интервал для среднего значения признака в генеральной совокупности, приняв доверительную вероятность равной 0,95.

1. Среднее значение признака в выборке равно

2. Значение среднего квадратического отклонения составляет

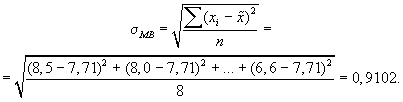
3. Средняя ошибка выборки:

4. Значение коэффициента доверия t  2,365 для п  8 и Р  0,95 (Приложение 1).

5. Предельная ошибка выборки:

6. Доверительный интервал для среднего значения признака в генеральной совокупности:

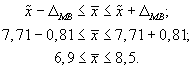
То есть с вероятностью 0,95 можно утверждать, что затраты времени студента на подготовку к контрольной работе находятся в пределах от 6,9 до 8,5 ч.