Задачи ЛП и методы их решения

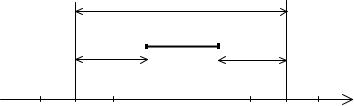
89

Определение. Резервом R(i) события i называется разность его позднего и раннего сроков.

♦

Для событий, лежащих на критическом пути, резерв равен разности Tпр − Tкрит , для остальных событий – больше этой разности.

Приведём все временные параметры событий в примере 1.

Временные параметры работ.

В отличие от событий, работа имеет протяжённость, т.е. связана с двумя событиями – своими началом и концом. Каждое из этих событий имеет два срока, поэтому у работы появляются 4 временных параметра по моменту начала и конца и 4 вида резервов. Полезна следую-

щая схема

Определение. Ранним началом tРН (i, j) работы ( i, j ) называется наименьшее время после начала проекта, через которое работу можно начать выполнять. ♦

Очевидно, работу можно начать, как только закончатся предшествующие работы, т.е. когда наступит событие i – событие начала. Отсюда

tРН (i, j) = tP (i) = yi .

91

Определение. Свободным резервом RC (i, j) работы ( i, j ) называется наибольшее время, на которое можно увеличить время работы, если предшествующие и последующие работы начинаются в свои ранние сроки. ♦

Коротко: "до нас и после нас рано".

Свободный резерв полностью определяется ранними сроками событий, не зависит от Tпр (это один из "внутренних" параметров проекта). Несложно получить (см. схему).

время, на которое можно увеличить время работы, если предшествующие и последующие работы начинаются в свои поздние сроки. ♦

Коротко: "До нас и после нас поздно".

RП (i, j) ≥ R′′(i, j) ≥ 0 .

Резерв второго рода – "внутренний" параметр (докажите это!).

Определение. Частным резервом первого рода R′(i, j) работы ( i, j ) называется наибольшее время, на которое можно увеличить время работы, если предшествующие начинаются и заканчиваются в поздние сроки, а последующие – в ранние сроки. ♦

Коротко: "до нас поздно, после нас рано".

R′(i, j) = tP ( j) − tП (i) − ti j .

Условия в определении этого резерва часто не выполняются, так как в случае, когда предшествующие работы заканчивались поздно, следующие за ( i, j ) могут уже не иметь возможности начинаться рано. Формально в этом случае частный резерв первого рода является отрицательным и показывает не запас, а нехватку времени для работы. В литературе встречается формула

R′(i, j) = max{tP ( j) − tП (i) − ti j ; 0}. В любом случае справедливы соотношения

RC ≥ R′ , R′′ ≥ R′ ,

т.е. R′ наименьший среди резервов.

Частный резерв первого рода – "внешний" параметр.

Из расчётных формул для резервов можно получить полезное соотношение

RП + R′ = RC + R′′ ,

позволяющее вычислить любой из резервов, если остальные три известны. Приведём полную таблицу параметров работ в примере 1.

92

Диаграмма Гантта.

Сетевой график неудобен для отслеживания процесса выполнения работ во времени, т.е. для календарного плана. На практике для графического изображения хода выполнения работ используют диаграммы Гантта (другие названия – линейные диаграммы, временные диаграммы и пр.)

Определение. Диаграмма Гантта – изображение работ проекта в виде прямолинейных горизонтальных отрезков, параллельных оси времени (оси абсцисс). Левый конец отрезка соответствует моменту начала работы, правый – окончания работы, длина отрезка равна времени работы. Взаимное расположение отрезков согласовано с отношением предшествования работ.

Проект имеет много диаграмм Гантта (бесконечно много), так как работа может начинаться от своего раннего начала до позднего начала. Можно выделить диаграмму Гантта по ранним срокам, или раннюю диаграмму Гантта, а также диаграмму Гантта по поздним срокам –

позднюю диаграмму Гантта.

На ранней диаграмме:

1)концы отрезков расположены в раннем начале и в раннем окончании работы;

2)RП определяется как максимальное значение времени, на которое работу можно сдвинуть

вправо, сдвигая также по необходимости другие работы (другие отрезки), до момента Tпр ;

3) RC – максимальное значение времени, на которое отрезок работы можно сдвинуть вправо, не сдвигая другие работы и не сдвигая момент окончания проекта Tкрит ;

4)Критические работы образуют непрерывную цепочку отрезков, и поэтому признак могут быть найдены по диаграмме;

5)Самый правый из концов отрезков расположен в момент Tкрит .

93

Свойства поздней диаграммы Гантта вполне аналогичны. Нужно только вместо "вправо" читать "влево", вместо RC рассмотреть R′′ и т.д..

94

7. ДОБАВЛЕНИЯ

Ниже излагаются необходимые сведения о теоретических положениях, дающих обоснование основному методу решения задач линейного программирования - методу последовательного улучшения плана и его алгоритмическим реализациям: прямому и модифицированному алгоритмам симплекс-метода. Используются “алгоритмические“ обозначения индексных множеств и индексов, заимствованные из книги И.В.Романовского [ 9 ], которые он впервые широко использовал в экстремальных задачах и характерные для Санкт-Петербургской школы исследования операций.

7.1. Векторы и матрицы

Можно рассматривать вектор как упорядоченный набор чисел X = (x1 , x2 , x3 , , xn )

где xi (множество вещественных чисел) - его компоненты

i 1: n- индексы его компонент

Если иметь в виду, что индексы (номера) компонент могут идти не подряд, и вообще могут быть не обязательно элементами числового множества от 1 до какого-либо n, то удобно в обозначении вектора иметь множество индексов его компонент. Обозначив такое конечное множество через N, можно рассматривать вектор Х, как функцию, заданную на этом конечном множестве.

X : N → X[N] : i N ! x[i] X[N]

Будем в дальнейшем обозначать вектор через X [ N ] , а множество индексов его компонент

Далее (см. вышеприведенные примеры):

2 N ' = {10}, X[N ' ] = x[10] = 9

3N ' = {6,9,2}, X[N ' ] = (4,−5,8)

4N ' = {слон,гиря}, X[N ' ] = (20000,1)

Скалярное произведение векторов в данных обозначениях записывается в виде

C[N] X[N] = ∑c[ j] x[ j]

j N

или с учетом разделения векторов на части(N ' N)

C[N] X[N] = C[N ' ] X[N ' ] + C[N \ N ' ] X[N \ N ' ]

96

Справедливо также равенство

E[M, N ' ]- единичная квадратичная матрица, для которой справедливы соотношения

E[M, N ' ] X[N ' ] = X[M ]

U[M ] E[M, N ' ] = U[N ' ]

В дальнейшем (если не оговорено заранее) будем считать, что

M = {1 2 m}, N = {1 2 n}

Векторы (набор векторов, систему векторов) будем называть линейно-независимыми, если равенство

С учетом обозначений S ={1,2, , s}, A[M, S] = {A1[M ], A2 [M ], , As [M ]}, λ[S] ={λ1 ,λ2 , ,λs }равенство (*) записывается в виде

(+) A[M, S] λ[S] = 0[M ]

т.е. однородная система с матрицей A[M , S] имеет только тривиальное (нулевое) решение. Если же система (*) (или (+)) имеет нетривиальное (ненулевое) решение, то вектора, составляющие матрицу A[M , S] будут линейно-зависимыми.

Если количество линейно независимых векторов-столбцов, образующих матрицу

A[M , S] совпадает с числом ее строк (т.е. M = S ), говорят, что вектора {A1[M ], , As [M ]}

(столбцы матрицы A[M , S]) образуют базис в пространстве векторов размерности m = M , а сама матрица (квадратная) называется невырожденной (неособой, базисной) матрицей.

Любая невырожденная матрица A[M, N ' ], ( N ' = M ) имеет обратную матрицу ,

B[N ' , M ] определяемую соотношениями

A[M, N ' ] B[N ' , M ] = E[M, M ]

B[N ' , M ] A[M , N ' ] = E[N ' , N ' ]

Вдальнейшем будут использоваться следующие стандартные обозначения и термины: Система уравнений с матрицей коэффициентов А, вектором правой части b

относительно вектора неизвестных X

(**) A[M, N] X[N] = b[M ]

(будем считать, что все строки матрицы A[M , N]], линейно независимы).

97

Базисное множество индексов N ' - N ' N : столбцы матрицы A[M , N ' ] образуют базис

Базисная матрица - A[M , N ' ]

Небазисная часть матрицы A[M, N] - матрица A[M, N \ N ' ]

Матрица обратная к базисной

(или обратная базисная матрица) - B[N ' , M ] : B[N ' , M ] A[M , N ' ] = E[N ' , N ' ]

Матрица коэффициентов разложения столбцов исходной матрицы по текущему базису - матрица Z[N ' , N] = B[N ' , M ] A[M, N] = (B[N ' , M ] A[M , N ' ], B[N ' , M ] A[M, N \ N ' ]) =

= (E[N ' , N ' ], Z[N ' , N \ N ' ])

Базисное решение системы (**) - вектор

X[N ' ]: A[M, N ' ] X[N ' ] = b[M ],(т.е.X[N ' ] = B[N ' , M ] b[M ])

X[N]:

' = '

X[N \ N ] 0[N \ N ]

( X[N ' ], X[N \ N ' ] - соответственно базисная и небазисная части базисного решения).

hБазисное множество индексов N ' далее для кратности (когда это не будет вызывать недоразумений) будем называть базисным множеством, базисом индексов или даже просто базисом, имея в виду, что базис образуют столбцы матрицы с множеством индексов N ' h

7.2. Постановка задачи ЛП

(Требуется найти экстремум (max или min) линейной функции C[N] X[N] от переменных X[N] (a), на которые накладываются ограничения в виде линейных неравенств (b) или

уравнений (с), и часть из которых X[N1 ] удовлетворяют ограничениям неотрицательности (d), а оставшаяся часть X[N2 ] свободна от этих ограничений (е)).

С помощью замены знака целевой функции и обеих частей любого ограничения, введения дополнительных переменных и использования факта о том, что любая величина может быть представлена в виде разности двух неотрицательных, произвольная ЗЛП может быть записана в стандартной форме

hОграничения равенства в общей форме ЗЛП называются жесткими ограничениями (это (с)), а ограничения-неравенства носят названия нежестких ограничений (это (в))h

98

Далее всюду (кроме оговоренных случаев) будем рассматривать ЗЛП в форме (I), предполагая, что все строки матрицы A[M, N] будут линейно независимы.

Множеством допустимых значений ЗЛП будем называть множество

D ={X[N]: A[M, N] X[N] = b[M ], X[N] ≥ 0[N] } ( + )

Базисным решением ЗЛП (с базисом индексов N ' ) будем называть допустимое решение ЗЛП X 0 [N] , являющееся базисным решением системы

A[M, N] X 0 [N] = b[M ]

с базисной матрицей A[M , N ' ] .

Базисное решение X 0 [N]будет невырожденным, если

X0 [N ' ] > 0[N ' ],

ивырожденным в противном случае

hДля простоты изложения, почти везде будем предполагать, что все базисные решения ЗЛП являются невырожденнымиh

7.3. Выпуклость множества допустимых решений ЗЛП

Множество V называется выпуклым, если оно вместе с любыми двумя своими точками целиком содержит отрезок, их соединяющий. Другими словами из условий

x1 V, x2 V x = λx1 + (1− λ)x2 V, 0 ≤ λ ≤1 Имеет место следующее утверждение:

Множество D допустимых решений ЗЛП является выпуклым

Доказательство

Возьмем два произвольных допустимых решения X1[N], X 2 [N] D

X1[N] D A[M , N] X1[N] = b[M ], X1[N] ≥ 0[N] X 2 [N] D A[M , N] X 2 [N] = b[M ], X 2 [N] ≥ 0[N]

Рассмотрим X[N] = λX1[N] + (1− λ)X 2 [N] , (0 ≤ λ ≤1) Покажем, что X[N] D

1)A[M, N] X[N] = A[M , N] (λX1[N]+ (1− λ)X 2 [N])=

= λA[M, N] X1[N]+ (1− λ)A[M, N] X1[N] = λb[M ]+ (1− λ)b[M ] = b[M ](λ +1− λ) = b[M ]

2) т. к. X1[N] ≥ 0[N] и λ ≥ 0 λX1[N] ≥ 0[N]

X 2 [N] ≥ 0[N] и (1− λ) ≥ 0 (1− λ)X 2 [N] ≥ 0[N] X[N] = λX1[N] + (1− λ)X 2 [N] ≥ 0[N]

■

Крайней точкой (угловой точкой или вершиной) выпуклого множества D называется точка Х данного множества не представимая в виде