FIT_Fizika_2-3

Рассмотрим работу, совершаемую полем над движущимися зарядами. Мощность этой работы, отнесенная к единице объема, равна

Р = Е - j .

Плотность тока можно выразить из одного из уравнений Максвелла:

Подставляя эту плотность тока в выражение для мощности и отнимая нулевой член, получающийся из другого уравнения Максвелла

Р = — (E-rotH — H-rotE)— — ( e - ^ + H - ^ Y

Вспоминая одну из формул векторного анализа

div{A xB) = B rotA — A - rotB

и вводя обозначения

окончательно приходим к формуле

^ + div S = —P. dt

Полученную формулу можно интерпретировать как локальный закон сохранения энергии электромагнитного поля. Действительно, запишем его в интегральной форме, для какого-либо объема V, окруженного замкнутой поверхностью Z. Используя теорему Остроградского-Гаусса, получаем

S- dZ.

Величина w есть плотность энергии электромагнитного поля, интеграл от нее - энергия поля в объеме V, следовательно - левый член выражения есть скорость изменения энергии поля в объеме V. Первый член в правой части есть убыль энергии поля вследствие произведенной им работы над зарядами. Второй член, очевидно должен иметь смысл потока энергии поля наружу, через окружающую объем поверхность Z. Отсюда окончательно получаем, что S есть плотность потока энергии электромагнитного поля; это выражение называют вектором Пойнтинга.

31

1.11 Электромагнитные волны

Перейдем к подробному изучению электромагнитных волн. Общее рассмотрение является весьма сложной проблемой, поэтому ограничимся случаем однородной непроводящей среды без зарядов и токов (или вакуумом). При этом

а. р(г) = 0, J(r) = 0;

б. = COnst.

Уравнения Максвелла и материальные уравнения среды в этом случае

_ 1 дВ 1. _ _

rot Е = — —, divB = 0,

с d t

rotH = -^, divD = 0,

с d t

D = sE, В = дН.

Возьмем частную производную по времени от 1-го уравнения 2-ой пары, и, поменяв порядок дифференцирования (не забывайте, что ротор есть дифференциальная операция, действующая на пространственные координаты) и используя 1-го уравнение 1-ой пары, получим:

Вспоминая проведенную выше формулу ротора от ротора и 2-го уравнения 2-ой пары, окончательно получаем

ДЕ — НЁ!^.

с at2

Аналогичное уравнение описывает и магнитное поле:

ЛИ - ^ = 0 .

с2 d t 2

Такие уравнения называют волновыми уравнениями. Задолго до создания теории Максвелла, подобное уравнение было получено и исследовано в механике и акустике. Впервые же это было сделано учеными Д'Аламбером и Эйлером при изучении упругих колебаний струны. На этом курсе мы также получали и решали скалярное одномерное волновое уравнение при изучении распространения волн в длинных линиях.

Если ввести оператор Д'Аламбера

1 d 2

□ = Д — v2 dt2’

то волновые уравнения для полей представимы в виде

□Е = 0, □Н = 0, v = -^=.

32

Плоские волны

Наиболее просто решение волнового уравнения выглядит в случае, если все величины зависят только от одной декартовой координаты, например, от z, а при изменении других координат не изменяются. Тогда

f(x, 0 = /i(z - vt) +f2iz + vt),

где ft и f2 - произвольные функции, ft описывает волну, двигающуюся вдоль оси z в положительном направлении, а /2 - в отрицательном направлении.

Далее будем рассматривать только волны, распространяющиеся в положительном направлении. Для плоского случая запишем 1-е уравнения обоих пар системы уравнений

J x

Множители при одинаковых ортах должны быть равны, что дает систему дифференциальных уравнений в частных производных. Сразу запишем решение этой системы, причем все константы интегрирования, как тривиальные и не влияющие на распространение электромагнитных колебаний, положим равными нулю:

Ex = E1{z-vt), Hx = —^E2{z — vt),

Еу = E2{z — vt), Hy = J^E±(z- vt),

Ez = 0, Hz = 0.

Можно сделать следующие выводы:

1. Колебания происходят в плоскости, перпендикулярной направлению распространения волны (поперечные колебания);

33

2.Вектора Е и Н перпендикулярны друг другу и образуют взаимно перпендикулярную тройку векторов вместе с вектором вдоль направления распространения волны;

3.По разным поперечным направлениям амплитуда колебаний различна. Эта характерная особенность электромагнитных колебаний называется поляризацией;

4.Энергия полей одинакова, поскольку ЕЕ2 = у.Н2.

Сферические волны

Если волна изотропно расширяется от точечного источника или сходится к нему, то в сферической системе координат с источником в центре компоненты полей, в силу симметрии задачи, не будут зависеть от угловых координат. Решение волнового уравнения следует искать в виде

f = f(r, t),

а само волновое уравнение в силу

д = д = дв

д<р 0

преобразуется к виду

Перенеся г в правую часть и занеся его под частную производную по времени, получаем уравнение, аналогичное рассмотренному для плоской волны:

Его решение

t) = A(r~Q + fzir + vt)

Плоские монохроматические волны

Важнейшим частным случаем плоских волн является их гармоническая зависимость от времени:

Eli2~cos{k(z — vt) + ^1,2) = cos(k • r — <i>t + <p12).

Введенный вектор k называют волновым вектором, направлен вдоль направления распространения волны. Модуль волнового вектора /с = |к| называют волновым числом, оно связано с частотой ш и пространственной длиной волны колебаний Я следующими соотношениями:

ш = kv, k = =^-.

А

Пусть

Ex{z, t) = Е± cos(kz — u>t),

34

Ey{z, t) = E2 cos(kz — Mt + ф).

Из выражений для Ех и Еу можно исключить зависимость от времени и координаты; при этом получится следующее выражение:

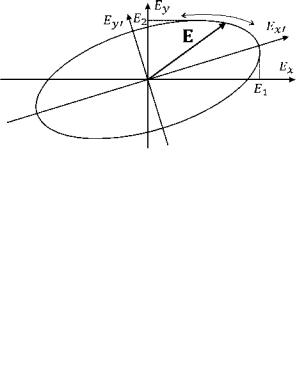
Это выражение в общем случае задает на плоскости координат Ех и Еу эллипс. Давайте зафиксируем какую-либо точку пространства с координатой z и будем измерять значение электрического поля в этой точке. Оказывается, что на плоскости ЕхЕу вектор Е направлен из начала координат в какую-либо точку на этом эллипсе (см. рис. 28). При изменении времени конец вектора Е движется вдоль эллипса. Направление движения зависит от значения фазы Ц): при Ц) от 0 до п движение происходит против часовой стрелки, при Ц) от п до 2п - по часовой стрелке. То же происходит и при фиксированном моменте времени при изменении точки наблюдения вдоль z.

Рисунок 28. Изменение во времени вектора электрического поля монохроматической волны при фиксированном положении точки наблюдения.

Чтобы не рассматривать различные значения Ц), сразу заметим, что уравнение любого эллипса можно преобразовать в канонический вид (не содержащий перекрестных членов) поворотом координат. Действительно, в нашем случае строго определено только направление оси z - вдоль направления распространения колебаний. Повернем оси х и у таким образом, чтобы компоненты полей удовлетворяли уравнению

амплитуды Elf и Е2, будут зависеть от Ег, Е2 и ф; точное выражение этой зависимости можно найти в соответствующем курсе математики. Существенно важно, что есть общий случай Е1г Ф Е2,; при этом говорят об эллиптической поляризации электромагнитной волны. Кроме того, выделяют два частных случая

- линейную поляризацию, при которой одна из амплитуд Elf или Е2, равна нулю и колебания происходят только вдоль одного поперечного направления (плоскости поляризации), и круговую поляризацию, когда Elf = E2f. Отметим, что для линейной поляризации разность фаз Ц) должна быть равна нулю или кратна п. Круговая поляризация имеет место при условии ф = п/2 + пп, Ег = Е2.

35

огибающая векторов электрического поля

Рисунок 29. Линейная и круговая поляризация электромагнитной волны.

Сравнение линейной и круговой поляризаций электромагнитной волны показано на рисунке 29. Стрелками показан вектора электрического поля в разных точках пространства вдоль линии распространения волны, красная линия - огибающая этих векторов. Кроме того, на рисунке показаны огибающие колебаний поля по двум поперечным направлениям. Видно, что для линейной поляризации фазы этих колебаний совпадают, для круговой - отстоят на п/2.

В дальнейшем нам пригодится тот факт, что любую эллиптически поляризованную волну можно представить как сумму двух линейно поляризованных волн с перпендикулярными плоскостями поляризации, или как сумму двух волн с круговой поляризацией, но с противоположными направлениями вращения вектора Е (левая и правая поляризации).

Стоячие волны

Рассмотрим суперпозицию двух монохроматических волн одинаковой частоты, распространяющихся навстречу друг другу. Будем считать, что они линейно поляризованы, их плоскости поляризации совпадают (пусть колебания происходят вдоль оси х), и они имеют одинаковую амплитуду.

Elx(z, t) = Е0 cos(kz — u>i), E2X (Z, t) = E0 cos(kz + wt + ^).

В силу принципа суперпозиции, итоговое поле есть сумма этих полей:

Ex = Elx + Elx = 2E0cos (kz + ^ cos (wt + j).

Такая волна не является бегущей, в ней нет члена kz ± шЬ. Напряженность во всех точках пространства изменяется с одинаковой частотой и в той же фазе; амплитуда колебаний меняется вдоль оси z по гармоническом закону. Такая волна называется стоячей. Мгновенные снимки бегущей и стоячей волн совпадают, но их динамика во времени различается кардинально.

Отметим, что при сложении двух волн, бегущих в одном направлении, получается опять бегущая волна.

36

Часть II Оптика

2.1 Отражение и преломление электромагнитных волн

Выше мы рассмотрели распространение плоской монохроматической волны в однородной среде. Такую волну можно представить в виде двух линейно поляризованных волн:

где вектора Ех и Е2 перпендикулярны и друг другу, и вектору к, причем направление вектора Ej_ (и, вместе с ним, вектора Е2) можно выбрать в плоскости, перпендикулярной к, произвольно. При этом, как и для любой свободной волны в изотропной среде, вектор Н перпендикулярен вектору Е.

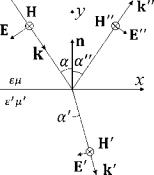
Рисунок 30. Падение электромагнитной волны на плоскую границу двух сред.

Рассмотрим поведение волны при ее падении на плоскую границу раздела двух оптически прозрачных сред с различными значениями s и ^. Вы уже изучали, что часть волны при этом отразится от границы раздела, часть - пройдет из первой среды во вторую; эти волны изображены на рисунке 30. Давайте рассмотрим этот вопрос подробнее. Вопервых, выделим плоскость падения - плоскость, образованную векторами к и п, где п есть единичный вектор нормали к границе раздела сред. Во-вторых, представим падающую волну как сумму двух линейно поляризованных волн; вектор Е одной из этих волн лежит в плоскости падения, вектор Е другой волны перпендикулярен этой плоскости. Для последующих рассуждений важно, что эти две волны можно рассматривать независимо друг от друга. Для первой волны вектор Н перпендикулярен плоскости падения, такую волну называют TM-волной (Transverse Magnetic), именно этот случай представлен на рисунке 30. Вторую волну называют TE-волной

37

(Transverse Electric). Так же поляризацию TM-волны называют р-поляризацией, а поляризацию TE-волны - s- поляризацией.

На предыдущих курсах при рассмотрении границы раздела двух сред вы получали граничные условия, связывающие величины электрического и магнитного полей во одной среде (непосредственно перед границей) с соответствующими величинами во второй среде (непосредственно за границей). В рассматриваемом случае отсутствия свободных зарядов и токов проводимости плотности поверхностного заряда ст и плотность поверхностного тока i равна нулю в каждой точке границы, и граничные условия приобретают следующий вид:

Dm = D2п, ^1т = ^2т, В1п = , Н1т = Н2т.

Рассмотрим TE-волну. Будем обозначать величины, относящиеся к волне, прошедшей во вторую среду, с одним штрихом, а величины, относящиеся к отраженной волне - с двумя штрихами. Из граничного условия для вектора Е следует

Јo6i(k-r-wt) + Eg k"-r-w"t) = Ј^ei(k'-r-w't)

Это условие должно выполняться в каждый момент времени для каждой точки границы раздела. Такое возможно, если только

ш = од' = од", к • г = к' • г = к" • г.

Следовательно, получаем первый вывод - частоты всех трех волн равны. Если взять в качестве г вектор еу - единичный вектор, перпендикулярный плоскости падения, то из второго условия получим

ку = ку = ку =0.

Вывод номер два - все три волновых вектора лежат в плоскости падения. Если в качестве г взять вектор ех, лежащий в плоскости падения и направленный вдоль границы так, что ех • к > 0, то второе условие примет вид

к sin(a) = к' sin(a') = к" sin(a").

Поскольку модуль волнового вектора определяется только частотой и параметрами среды к = ш/v = ш[Ё^/с, то к = к", следовательно, sin(a) = sin(a"). Вывод номер три - угол падения равен углу отражения. Отсюда же получаем вывод номер четыре - связь угла падения с углом преломления:

sin(a) _ к’ _ ^£гц.' _ п' sin(a') к [Щ п ’

здесь мы ввели величину п = [ЁЦ - показатель преломления среды. Эту связь так же называют законом Снеллиуса.

Полностью аналогичные выводы для TM-волны дает рассмотрение граничных условий для поля Н. Следовательно, полученные соотношения справедливы для падающей волны любой поляризации.

38

Приведенные выше соотношения не дают ответа на вопрос о величине амплитуд отраженной и преломленной волн. Рассмотрим TM-волну. Из граничных условий для векторов Е и Н следует

Е cos(a) — Е" cos(a") = Е' cos(a'), Н + Н" = Н'.

Вспоминая соотношение между величиной электрического и магнитного поля в плоской волне, закон Сенллиуса, учитывая равенство углов падения и отражения, а так же то обстоятельство, что в большинстве сред д ~1, получаем:

Решая эту систему алгебраических уравнений относительно неизвестных Е' и Е", находим: g, = g 2sin(a')cos(a)

sin(a+a')cos(a-ar y

Аналогично для TE-волны находим используя те же граничных условий

Полученные соотношения между амплитудами падающей, отраженной и преломленной волн называют формулами Френеля. Оказывается, эти соотношения разные для разных поляризаций падающей волны. На основе формул Френеля можно рассчитать коэффициенты отражения и пропускания, которые равны отношению потока энергии в отраженной и преломленной волнах соответственно к потоку энергии падающей волны. Эти коэффициенты обозначаются как R и Т =1 — R и для разных поляризаций равны

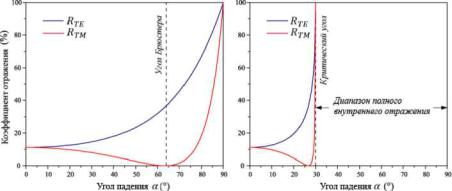
Рисунок 31. Зависимость коэффициента отражения от угла падения.

Рассмотрим зависимость коэффициентов прохождения от угла падения при п'/п >1 и п'/п < 1, графики которой представлены на рисунке 31 . Вопервых, можно заметить, что существует угол падения, при котором RTM = 0 - одна из поляризаций исчезает! Если на поверхность под этим углом падает

39

волна, имеющая эллиптическую поляризацию, то отраженная волна будет линейно поляризована, причем вектор Е в ней будет перпендикулярен плоскости падения. Этот угол называют углом Брюстера; обозначим его через аБ. Условие, которому он должен удовлетворять

= п'/п.

Из закона Снеллиуса

sin(aБ) = sin^a^^ = cos(a:B).

Отсюда получаем, что аБ + аБ = п/2.

Во-вторых, видно, что для случая п'/п < 1 есть ограничение для угла падения. Точнее, конечно, угол падения может быть любой, но тогда из закона Снеллиуса следует, что в случае, если sin(a) > п'/п синус преломленного угла равен

sin(ar) = sin(a)^ > 1.

п'

Такое возможно только при комплексном угле а'. Разумеется, все реальные углы, образуемые световыми лучами с осями координат, остаются вещественными, но меняется физическая сущность происходящих процессов - преломленная волна отсутствует. Такой эффект называется полным внутренним отражением, т.е. при достаточно “косом” падении волна не может вырваться из более плотной среды, вся световая энергия возвращается обратно в первую среду. В частности, эффект миража возникает вследствие полного отражения между слоями воздуха с разной температурой. Критический угол падения, при котором наступает полное внутренне отражение, определяется из условия

sin(a') = 1, sin(aKp) = п'/п.

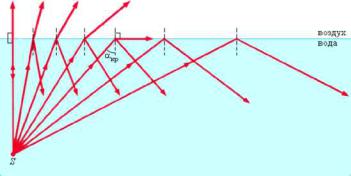
Поведение отраженного и преломленного лучей при различных углах падения из оптически более плотной среды и момент возникновения полного внутреннего отражения изображено на рисунке 32.

Рисунок 32. Поведение отраженного и преломленного лучей при различных углах падения.

Эффект полного внутреннего отражения находит многочисленные применения в оптических устройствах. Так, он используется в призмах, отклоняющих световой поток. Полное отражение используется также в оптических волокнах

40