
№1 Визуализация данных
.pdfприближенное решение — точка равновесия имеет координаты : x = 1.6;у = 3.25.
Построение плоскости.
MS Excel позволяет выполнять построение и пространственных объектов. Рассмотрим эту возможность на примере построения плоскости
Уравнение вида: |
|
Ах + Ву + Cz + D = 0 |
(1.1) |
называется общим уравнением плоскости.
Мастер диаграмм может быть также использован и для построения плоскостей. Для этого необходимо ввести точки плоскости в рабочую таблицу, вызвать Мастер диаграмм, задать тип диаграммы, диапазоны данных и подписей оси.
Пример 1.5. Рассмотрим построение плоскости в Excel, если она задана уравнением вида (1.1):
2·х – 4·у – 2·z + 2 = 0.
Пусть необходимо построить часть плоскости, лежащей в первой четверти х
[0; 6] с шагом h1 = 0.5, .у [0; 6] с шагом h2 = 1).
Решение. Вначале необходимо разрешить уравнение относительно переменной
z.В нашем примере z =·х – 2·у + 1.
1.Введем значения переменной х в столбец А (начиная с ячейки А2).
2.Значения переменной у вводим в строку 1 (начиная с ячейки В1).
3.Далее вводим значения переменной z. В ячейку В2 вводим ее уравнение = $A2 + 2*В$1 + 1. Обращаем внимание, что символы $ предназначены для фиксации адреса столбца А — переменной х и строки 1 — переменной у. Затем автозаполненнем копируем эту формулу вначале в диапазон В2:Н2. после чего — в диапазон ВЗ:Н14 (протягиванием вниз)
4.В результате должна быть получена следующая таблица (рис.1.13).
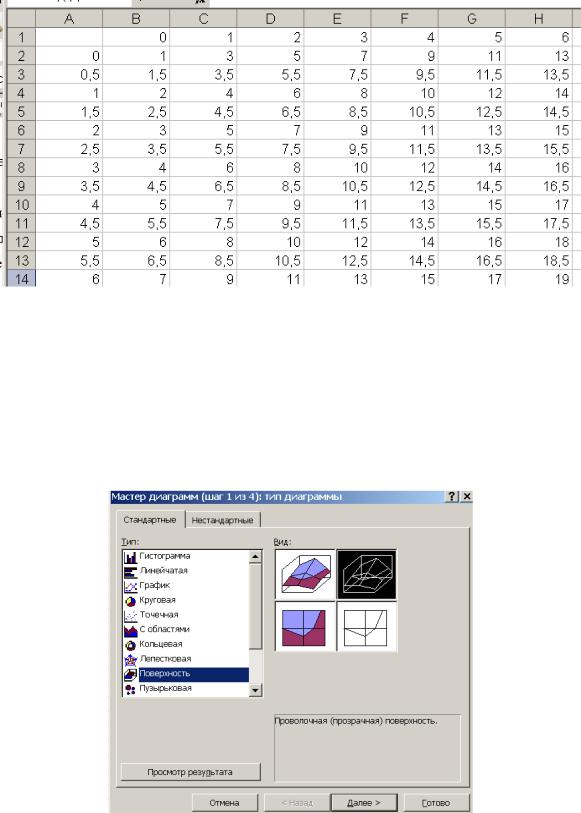
Рис.1.13 5. Выделяем мышью диапазон А1:Н14. Обращаемся к Мастеру диаграмм.
В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): тип диаграммы указываем тип диаграммы – Поверхность, и вид — Проволочная (прозрачная) поверхность (правую верхнюю диаграмму в правом окне). После чего нажимаем кнопку Далее.
Рис.1.14
6.В этом примере переключатель Ряды установим в положение «в столбцах». Затем указываем название диаграммы и осей. Полученная диаграмма имеет вид (рис.1.15)
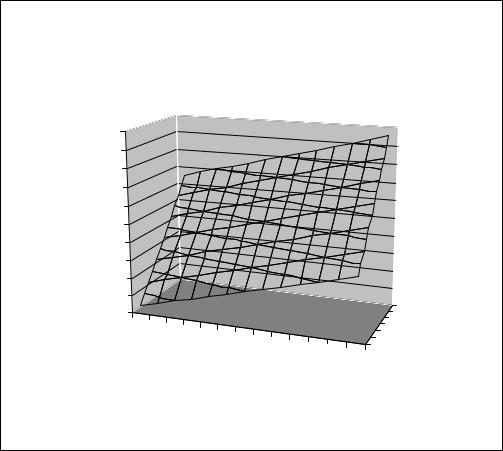
Плоскость
20
18
16
14
12
значения z 10 8 6 4 2 0
0 |
1 |
2 |
3 |
4 |
5 |
6 |
значения y
6
3 значения x
0
Рис.1.15
2. Решение уравнений с помощью процедуры «подбор параметра».
В MS Excel для решения уравнений вида f(x) = 0 используется удобный и простой для понимания инструмент Подбор параметра.
Процесс решения с помощью процедуры Подбор параметра распадается на два этапа:
1.Задание на рабочем листе ячейки, содержащей значение независимой переменной решаемого уравнения (так называемой влияющей ячейки), и ячейки содержащей формулу уравнения (зависящей или целевой ячейки).
2.Ввод адресов влияющей и целевой ячеек в диалоговом окне Подбор параметра и получение ответа (или сообщения о его отсутствии или
невозможности нахождения, поскольку уравнение может не иметь решений или алгоритм решения (оптимизации) может оказаться
расходящимся в конкретных условиях). Рассмотрим этот процесс на конкретном примере. Пример 2.1. Найти решение уравнения ln(x)=0. Решение:
Первый этап
1.Открываем новый рабочий лист (команда Вставка → Лист).
2.Заносим в ячейку А1 ориентировочное значение корня, например, 3.
3.Заносим в ячейку В1 левую часть уравнения, используя в качестве независимой переменной ссылку на ячейку Al. Для этого нажимаем на панели инструментов Стандартная кнопку Вставка функции; в появившемся диалоговом окне Мастер функций в рабочем поле
Категория выбираем Математические, а в рабочем поле Функция имя функции LN. После чего щелкаем на кнопке ОК; в рабочее поле Число щелчком мыши на ячейке А1 вводим ее адрес. Затем, нажимаем на кнопку ОК.
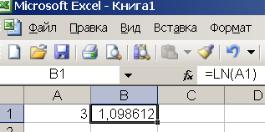
Вячейке В1 появляется число 1,098612(рис.2.1).
Рис.2.1
Второй этап
1.Вызываем процедуру Подбор параметра (команда Сервис → Подбор параметра).
2.В поле Установить в ячейке мышью указываем В1, в поле Значение задаем 0 (правая часть уравнения), в поле Изменяя значение ячейки мышью указываем на А1 (рис.2.2).

Рис.2.2
3.Щелкаем на кнопке ОК и получаем результат подбора, отображаемый в диалоговом окне Результат подбора параметра. Щелкаем на кнопке ОК. чтобы сохранить порученные значения ячеек, участвовавших в операции. В ячейке Al получаем приближенное значение х = 0,999872 (рис.2.3). При этом обратим внимание на погрешность решения (значение правой части уравнения) — вместо 0 в ячейке В1 получаем - 0,00013.
Рис.2.3
Таким образом, при значении х = 0,999872 правая часть уравнения lп(х) = 0 приближается к нулю (-0,00013). Принимая во внимание, что полученный корень это приближенное решение, его можно округлить до 1, то есть х = 1, что и является известным аналитическим решением этого уравнения.
При решении уравнений, имеющих несколько действительных корней, имеет смысл предварительно построить график левой части (функции f(x) ). Это позволит правильно подобрать начальные значения параметра.
Пример 2.2. Найти решение уравнения х2 - 4х +2 = 0. Решение.
1. Строим график функции y = х2 - 4х +2 (рис.2.4).

|
7 |
|
|
|
6 |
|
|
|
5 |
|
|
|
4 |
|
|
|
3 |
|
|
|
2 |
|
|
|
1 |
|
|
|
0 |
|
|
2 |
-1 0 |
2 |
4 |
|
-2 |
|
|
|
-3 |
|
|
|
|
Рис.2.4 |
|
Из него следует, что уравнение имеет два действительных корня Решение начинаем с нахождения первого корня.
2.Открываем новый рабочий лист (команда: Вставка → Лист).
3.Заносим в ячейку А1 ориентировочное значение первого корня, например, 3.
4.Заносим в ячейку В1 левую часть уравнения, используя в качестве независимой переменной ссылку на ячейку А1. Соответствующая формула будет иметь вид: =А1^2-4*А1+2.
5.Вызываем процедуру Подбор параметра (команда Сервис → Подбор параметра).
6.В поле Установить в ячейке указываем В1, в поле Значение задаем 0 (правая часть уравнения), в поле Изменяя значение ячейки указываем ячейку А1.
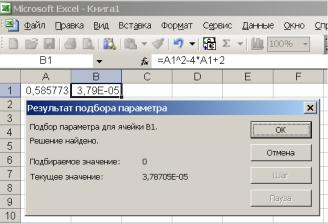
Рис.2.5
7.Щелкаем на кнопке 0К и получаем результат подбора, отображаемый в диалоговом окне Результат подбора параметра. Щелкаем на кнопке 0К, чтобы сохранить полученные значения ячеек, участвовавших в
операции. Таким образом, в ячейке А1 получаем приближенное значение
х1 = 3,414212 (рис.2.5).
При этом обратим внимание на точность решения (значение правой части уравнения): вместо 0 в ячейке В1 получаем: -5,7Е-06 (-0,0000057).
8.Повторяем расчет для второго корня х2, задавая в ячейке А1 другое начальное значение, например -3. Получаем значение второго корня уравнения х2 = 0,5857730 ; значение функции правой части для него равно
3,78705E-05 (рис.2.6)
Рис.2.6
1. Построить график функции.
Вариант |
Функция |
Диапазон, шаг |
1 |
Y=x2-1 |
[-3;3], 0.3 |
2 |
Y=x2+1 |
[-3;3], 0.3 |
3 |
Y=-2.5*x |
[-5;0], 0.2 |
4 |
Y=3*x+x2 |
[0;8], 0.5 |
5 |
Y=3*x2 |
[-5;5], 0.5 |
6 |
Y=3*x3 |
[-3;3], 0.1 |
7 |
Y=cos(x)+1 |
[0;2*Pi] |
8 |
Y=(x+3)/(x-2) |
[3;10], 0.2 |
9 |
Y=(x+8)/(x-4) |
[1;20], 0.5 |
10 |
Y=3+2/x+3/x2 |
[-3;-1], 0.1 |
11 |
Y=1/(x2-2*x+1) |
[-10;0], 0.2 |
12 |
Y=1/( x2-3*x-2) |
[-8;10], 0.2 |
13 |
Y=1+x2/(3+z2/5) |
[0;5], 0.5 |
14 |
Y=x4+4*x2-5 |
[-3;3], 0.3 |
15 |
Y=-3.1*x-x2 |
[-4;4]; 0.1 |
2. Построить графики функций в одной системе координат:
1 |
f1(x) = 2sin(x); |
f2(x) = sin(2x); |
f3(x) = f1(x) + f2(x) |
||
2 |
f1(x) = cos(2x); f2(x) = cos(3x); f3(x) = f1(x) + f2(x) |
||||
3 |
f1(x) = sin2(x); |
f2(x) = sin(x); f3(x) = f1(x) + f2(x) |
|||
4 |
f1(x) = cos(x2); |
f2(x) = cos(x); |
f3(x) = f1(x) + f2(x) |
||
5 |
f1(x) = sin(x); |
f2(x) = sin(x + π/4); f3(x) = f1(x) + f2(x) |
|||
6 |
f1(x) = cos(x); |
f2(x) = |cos(x)|; |
f3(x) = f1(x) + f2(x) |
||
7 |
f1(x) = sin(x); |
f2(x) = cos(x + π/4); f3(x) = f1(x) + f2(x) |
|||
8 |
f1(x) = 2sin(3x + 1.2); |
f2(x) = 3sin(2x + 0.6); |
f3(x) = f1(x) + f2(x) |
||
9 |
f1(x) = cos(2x + π/4); |
f2(x) = cos(1.5x - π/4); |
f3(x) = f1(x) + f2(x) |
||
10 |
f1(x) = 3sin(2x + π/6); |
f2(x) = 1.5sin(2x + π/4); f3(x) = f1(x) + f2(x) |
|||
11 |
f1(x) = sin2(x); |
f2(x) = cos3(x); |
f3(x) = f1(x) + f2(x) |
||
12 |
f1(x) = |cos(x)|; f2(x) = sin2(x); |
f3(x) = f1(x) + f2(x) |
|||
13 |
f1(x) = 2x3 - 9x2 + 1; f2(x) = lg(2+x) - 2x2 |
|
|||
14 |
f1(x) = 5x3 - x2 + 3; |
f2(x) = 2lg(x) |
|
||
15 |
f1(x) = x2 - 10x + 2; |
f2(x) = 5x3 - sin(x) |
|
||
