Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Киевский национальный университет технологий и дизайна

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Metodichka_dlya_zaochnik_2_sem (1)

.pdf

Скачиваний:

Добавлен:

04.02.2016

Размер:

515.54 Кб

Скачать

☆

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

Збіжними називають невласні інтеграли, якщо границі у формулі (26) існують, а якщо ці границі не існують, то невласні інтеграли називають

розбіжними.

+∞ x dx

Приклад 30. Дослідити на збіжність інтеграл

∫0

x2 +10

Розв’язання. Застосуємо першу з формул (26). Одержимо

+∞

x dx

= lim

lim

ln (x

+10)

0 x

+10

0 x

∫

b→+∞ ∫

b→+∞

lim

(

b2 +10

)

−ln10

)

(

ln (

+∞)

−ln10

)

∞ =∞.

2 b→+∞ (

Невласний інтеграл розбіжний.

Приклад 31. Дослідити на збіжність інтеграл +∞∫ 2 dx .

−∞ x +10

Розв’язання. На проміжку інтегрування (−∞, +∞) виберемо довільну точку.

Наприклад, x = 0 . Тоді будемо знаходити збіжність інтеграла на двох проміжках

(−∞,0) та (0, +∞). Одержимо

+∞

−∞∫

= −∞∫

+ ∫0

= alim→−∞ ∫a

+blim→+∞ ∫0

x2 +10

lim

arctg

+ lim

arctg

a→−∞

b→+∞

lim arctg 0 −arctg

lim

arctg

−arctg 0

10 a→−∞

10 b→+∞

(−arctg (−∞))+

arctg ∞ =

(arctg ∞+arctg ∞)=

arctg ∞ =

π =

7.4. Застосування визначених інтегралів до задач геометрії

Площу криволінійної трапеції	для неперервної на сегменті [a,b]	функції
y = f (x)> 0, згідно геометричного змісту інтеграла, обчислюють за формулою
S = ∫b	f (x)dx .	(27)
a

Площу криволінійного сектора в полярній системі координат обчислюють за формулою

		ϕ2	(ϕ)dϕ ,
S =	1	∫ρ2		(28)
S =	2	∫ρ2		(28)
		ϕ1

де ρ = ρ(ϕ) неперервна ϕ [ϕ1,ϕ2 ].

Довжину дуги лінії на сегменті [a,b] неперервної разом зі своєю похідною функції y = f (x) обчислюють за формулою

l = ∫b	1+(f ′(x))2 dx ,	(29)
a
або за формулою
t2	(xt′)2 +(yt′)2 dt ,
l = ∫	(xt′)2 +(yt′)2 dt ,	(30)
t1
якщо функція задана параметрично x = x(t ), y = y (t ),		t [t1 ,t2 ].
У випадку, коли крива задана полярним рівнянням ρ = ρ(ϕ), ϕ [ϕ1,ϕ2 ], то
ϕ
l = ∫1	ρ2 +(ρ′)2 dϕ .	(31)
ϕ2

Об’єм тіла обертання криволінійної трапеції з основою [a,b] навколо осі Ox ,

яка обмежена неперервною функцією y = f (x), обчислюється за формулою

	V =π∫b	y2 dx .	(32)
	a
Якщо криволінійна трапеція з основою [c, d ] обертається навколо осі Oy , то
об’єм тіла обертання обчислюють за формулою
	V =π∫d (ϕ(y))2 dy =π∫d x2 dy ,		(33)
	c	c
де x =ϕ(y)	неперервна y [c, d ].
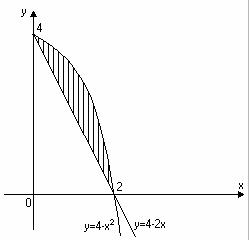
Задача	2. Обчислити площу фігури,	яка обмежена лініями	y = 4 − x2 та

y = 4 −2x .

Розв’язання. Зобразимо фігуру (рис. 10). Знайдемо точки перетину ліній. Для цього розв’яжемо систему:

y = 4 − x2 , 4 x2 4 2x x2 2x 0, x 0, x 2

y = 4 −2x, − = − − = 1 = 2 = .

Площа фігури дорівнює різниці площ двох криволінійних трапецій, площі яких обчислимо за формулою (27). Одержимо

S = S2 −S1 = ∫2 (4 − x2 )dx −∫2 (4 −2x)dx =

										0								0
		2									)				2	(				)
	=	∫(									)				∫	(		2x − x2		)	dx =
	=			4 − x2 −4 +2x dx =														2x − x2			dx =
		0													0
					x	2		x	3			2	8				4		(кв.од.)
						2			3			2
	=		2				−					= 4 −		=
Рис. 10	=		2				−					= 4 −	3	=			3
				2			3					0

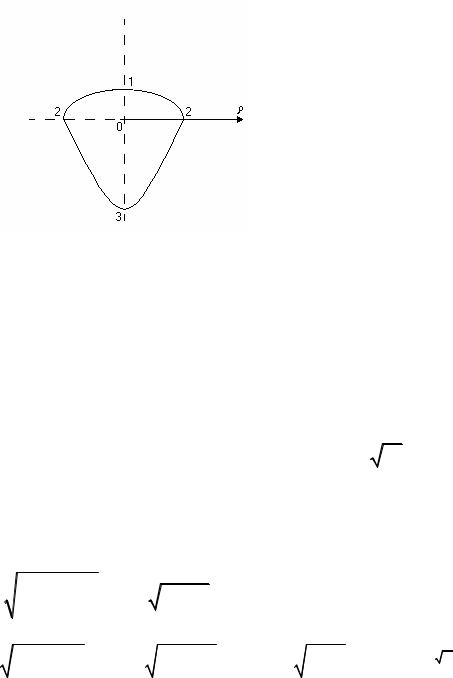
Задача 3. Обчислити площу фігури, яка обмежена лінією ρ = 2 −sinϕ .

Розв’язання. Побудуємо в полярних координатах лінію ρ = 2 −sinϕ по точках (рис. 11).

ϕ							ρ																																											Застосуємо															формулу						(28).
																																																		Застосуємо															формулу						(28).
																																													Одержимо
																																													Одержимо
	0						2																																																							2π
2							1																																															S = 2								∫(2 −sinϕ)							2	dϕ	=
	π																																																												1
π							2																																																							0
																																																														0
	3			π			3																																														=				1			2∫π (4 −4sinϕ +sin2 ϕ)dϕ =
	2																																																								1
	2																																																								2
2π							2																																														2π							0							1 −cos2ϕ
																																																				1	2π														1 −cos2ϕ
																																															=					1		4						−4sinϕ					+						dϕ =
																																															=					2		4						−4sinϕ					+						dϕ =
																																																					∫0																2
																								Рис. 11																													∫0																2
																								Рис. 11																													2π
																																																					2π
																																															=					1	∫(			9		−4sinϕ −								1		cos2ϕ)dϕ =
																																															=					2	∫(			2		−4sinϕ −								2		cos2ϕ)dϕ =
																																																					0
=			1		(	9	+4cosϕ −											1			sin 2ϕ)					2π			=				1	(	9		2π +4cos2π −												1		sin 4π −4cos0 +																1	sin 0)=
			1			9												1															1		9														1																		1
			2			2												4															2		2														4																		4
																											0
=			1		(2π +4 −4)=															9		π (кв.од.)
=			2		(2π +4 −4)=															2		π (кв.од.)
							Задача 4. Обчислити довжину дуги лінії y =																																														x3 , якщо x												[ ]
							Задача 4. Обчислити довжину дуги лінії y =																																														x3 , якщо x												0,1 .
							Розв’язування. Згідно формули (29)																																									необхідно														знати			похідну						функції.
Знайдемо y′ =																	1
														3		x					. Тоді
														3					2
														2					2																					(1+ 4					x)
1																	1																							(1+ 4					x)	3		1
1						1									2		1																											9		2		1
						1									2																															2
l = ∫							1+(		3		x	2	)				dx = ∫ 1+											9			x dx =								4									=
l = ∫							1+(		2		x	2	)				dx = ∫ 1+											4			x dx =								9	3								=
0																	0																										2					0
=		8					(1+	9		x)3					1			=					8	( (1+						9		)3 −1)=									8	( (134 )3 −1)=												8	(13 813 −1).
		8						9							1								8							9											8													8
		27						4															27							4											27													27
															0
							Задача 5. Обчислити довжину однієї арки циклоїди																																																				[				]
																							x = a		(		t		−sin t							)		,		(										)		,		t					[		0, 2π		]	.
																							x = a				t		−sin t									,		y = a 1−cos t												,		t							0, 2π			.

Розв’язування. Довжину дуги лінії обчислимо за формулою (30). Для цього знайдемо xt′ та yt′, а також (xt′)2 +(yt′)2 . Одержимо

xt′ = a(1−cos t ), yt′ = asin t, (xt′)2 +(yt′)2 = a2 (1−cos t )2 +a2 sin2 t =

=a2 (1−2cos t +cos2 t +sin2 t )= a2 (2 −2cos t )= 2a2 (1−cos t )=

=2a2 2sin2 2t = 4a2 sin2 2t ;

l =

2∫π

(xt′)2 +(yt′)2 dt =

2∫π

4a2 sin2

dt = 2a

2∫π sin

dt =

2π

= −2a 2cos

= −4a(cosπ −cos 0)= −4a(−1−1)=8a.

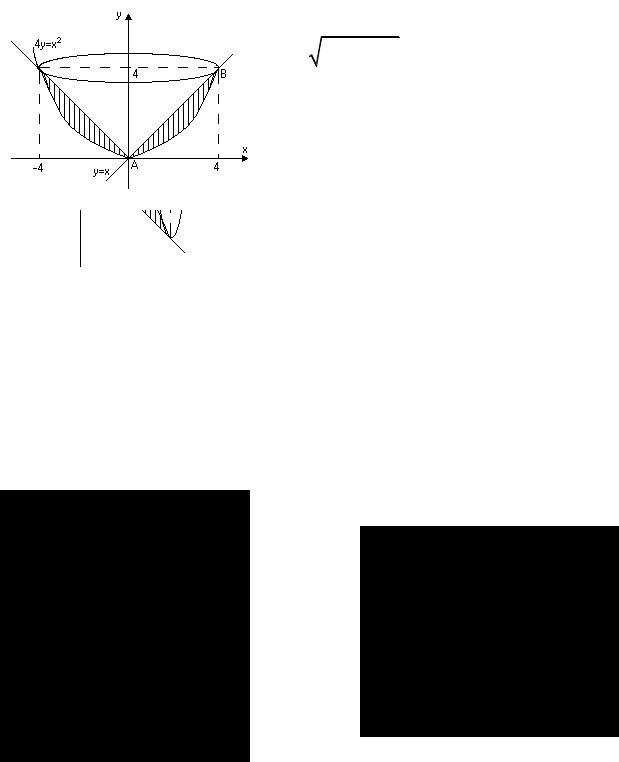
Задача 6. Обчислити об’єми тіл обертання навколо осей Ox та Oy фігури, яка

обмежена лініями 4 y = x2

та y = x .

Розв’язування. Обчислимо об’єми тіл, які утворюються при обертанні фігури

навколо осей. Знайдемо точки перетину ліній:

= x2 x2 −4x = 0, x(x

x = 0,

x = 4

4 y

−4)= 0, 1

y = x,

y1 = 0, y2 = 4.

Одержали

дві

точки з

координатами

A(0;0)

та B(4;4). Зобразимо ці тіла

схематично (рис. 12,13).

Рис. 13

Рис. 12

1) Об’єм тіла обертання навколо осі Ox дорівнює різниці двох об’ємів тіл, які ми обчислимо за формулою (32). Одержимо

V =V1 −V2 =π∫4 x2 dx −π∫4 (											x2	)2 dx =π					x3	4 −	π	∫4 x4 dx =
											4						3		16
					0					0								0		0
=	π x3	4 −		π		x5	4	=	π	64 −				π	45	=	64π −		64π		=


	3	0	16		5		0		3				16		5		3		5

()

=15 = 15 π (куб.од.)

2)Аналогічно обчислюємо об’єм тіла обертання навколо осі Oy ,64π 5 −3 128

використавши формулу (33):

V =V1 −V2 = −π∫4 y2 dy +π∫4 4 y dy = −π												y3		4 +4π	y2	4	=
V =V1 −V2 = −π∫4 y2 dy +π∫4 4 y dy = −π												3		4 +4π	2		=
							0		0			3		0	2	0
= 2π y2			4 −	π	y3			4	= 2π 16 −π	16 =	6π 16 −16π				=
				π				4			6π 16 −16π

			0	3				0	3				3
=	16π (	6 −1)			=	80			π (куб.од.)
=					=	3			π (куб.од.)
3						3

8.Функції багатьох (n ≥ 2) змінних

8.1.Частинні похідні і повний диференціал

Функцією двох змінних називається правило (закон), по якому кожній парі чисел (x, y) M відповідає єдине число z N . Множина M – область визначення функції, а N – множина значень функції.

Для функцій двох та багатьох змінних z = f (x, y), z = f (x1 , x2 ,..., xn )

розглянемо частинні похідні.

Частинною похідною функції z = f (x, y) по одній змінній називають скінченну границю виду:

lim	∆	x	z	=	∂z	= z′x = fx′(x, y);	lim	∆y z	=	∂z	= z′y = fy′(x, y),
					∂x			∆y		∂y
∆x→0	∆x						∆y→0
де ∆x z та ∆y z	– частинний приріст функції по одній змінній.
Повним	диференціалом функції						багатьох		змінних називається головна

лінійна частина приросту функції. Для функції z = f (x, y) повний диференціал має вигляд

dz = z′x dx + z′y dy .

Повний диференціал функції багатьох змінних застосовується до наближених обчислень, вважаючи, що ∆z ≈ dz .

Частинні похідні знаходяться за правилами та формулами диференціювання функції однієї змінної, вважаючи решту змінних сталими величинами.

Частинною похідною n-го порядку функції багатьох змінних по одній змінній називають першу похідну від n −1-ї похідної.

Приклад 32. Знайти частинні похідні другого порядку функції z = x5 y2 −2xy3 +3x −5 y +11.

Розв’язання. Знайдемо частинні похідні першого порядку по кожній змінній:

∂z	= z′x = 5x4 y2 −2 y3 +3,	∂z	= z′y = 2x5 y −6xy2 −5.
∂x		∂y

Від кожної частинної похідної першого порядку z′x та z′y знайдемо першу похідну по кожній змінній. Це будуть частинні похідні другого порядку і їх буде чотири:

∂2 z		= z′′2 = 20x3 y2		;	∂2 z	= z′′	=10x4 y −6 y2 ;
	2
∂x			x		∂x∂y	xy

∂2 z			= z′′yx =10x4 y −6 y2 ;			∂2 z	= 2x5 −12xy.
∂y∂x						∂y2

Мішані похідні, які відрізняються порядком диференціювання, z′′xy = z′′yx , рівні між собою. Ця умова виконується у випадку їх неперервності.

Приклад 33. Знайти ∂∂x2∂zy = z′′xy , якщо z = ln (x3 +2 y3 −2x +1).

Розв’язання. Знайдемо частинну похідну функції тільки по x або по y , а

потім від неї знайдемо першу похідну по іншій змінній. Одержимо

∂z

= z′x =

(3x

−2)=

3x2 −2

;

∂x

+2 y

−2x +1

+2 y

−2x +

∂2 z

= z′′xy =

0 −6 y2 (3x2 −2)

= −

6 y2 (3x2 −2)

(

)

(

)

∂x∂y

+2 y

−2x +1

+2 y

−2x +1

Задача 7. Знайти рівняння прямої y = ax +b методом найменших квадратів,

користуючись таблицею значень

					x		1			2	3		4	5		.

					y	0,02			1,97		4,01		5,96	7,92
	Розв’язання. Згідно методу найменших квадратів для знаходження параметрів
a і b прямої використовують систему рівнянь:
						a∑xi2 +b∑xi = ∑xi yi ,
							n			n		n
							i=1			i=1	i=1			(34)
									n		n			(34)
									n		n
							a∑xi +bn = ∑yi .
								i=1			i=1
Для простоти складання системи (34) складемо таблицю значень:
										55a +15b = 79, 43,
	xi	yi	2	xi yi
	xi	yi	xi	xi yi
								+		15a	+5b =19,88,				(−3)
								+
	1	0,02	1	0,02
	1	0,02	1	0,02
	2	1,97	4	3,94				10a = 79, 43 −3 19,88 = 79, 43 −59,64 =19,79,
	3	4,01	9	12,03				a =1,979;
	4	5,96	16	23,84				5b =19,88 −1,979 15 =19,88 −29,685 = −9,805,
	5	7,92	25	39,60				b = −1,961.

	∑15	19,88	55	79, 43

Відповідь. Рівняння прямої має вигляд y =1,979x −1,961.

8.2. Екстремум функцій двох змінних

Поняття екстремуму (максимуму і мінімуму) для функцій багатьох змінних аналогічне поняттю для функції однієї змінної.

Точка P0 (x0 , y0 ) D для функції z = f (x, y) називається точкою

максимуму, якщо для довільних точок із її околу виконується умова f (P0 )> f (P)

і точкою мінімуму, якщо f (P0 )< f (P).

Необхідними умовами існування

екстремуму функції z = f (x, y) в точці

P0 (x0 , y0 ) є умови

z′

(x , y

)=0,

z′ (x , y

)= 0.

(35)

Визначник виду

z′′2

z′′

∆ =

(36)

z′′

z′′2

для функції z = f (x, y) називається визначником Гессе або гессіаном.

Достатньою умовою існування екстремуму функції

z = f (x, y)

в критичній

точці P

(x , y

) є умова

∆(P )> 0 , і якщо

z′′2

(P )< 0 ,

то точка

є точкою

максимуму, а у випадку z′′2

(P )> 0 – точкою мінімуму. У випадку, коли

∆(P )<0,

ця умова є достатньою умовою відсутності

екстремуму в критичній точці P0 .

Сумнівним є випадок ∆(P0 )= 0 . Тоді необхідні додаткові дослідження.

Приклад 34. Знайти екстремуми функції z = x3 + y3 −27x −12 y .

Розв’язання.

Знайдемо

частинні

похідні

першого

порядку:

z′x

=3x2 −27, z′y =3y2 −12. В силу умови (35) прирівнюємо ці похідні до нуля і,

розв’язавши систему рівнянь,

знаходимо критичні точки функції.

−27

= 0,

−9

= 0,

x = ±3,

3y2

−12

= 0,

y2 −4

= 0,

y = ±4.

Одержали такі критичні точки: P1 (3;4),

P2 (3; −4), P3 (−3;4) і P4 (−3; −4).

Знайдемо

частинні

похідні

другого

порядку:

z′′2 = 6x, z′′ = 0,

z′′2

= 6 y, z′′ = 0 . Підставимо ці похідні у визначник Гессе (36). Одержимо

∆ =

=36xy .

6 y

Обчислимо значення цього визначника в кожній точці:

1)	P	(3, 4), ∆(P )=		18 0					=18 24 >			0, z′′2	(P )=18	> 0	,
	1		1	0				24				x	1
				0				24
P1 (3;4)	– точка мінімуму;
2)	P	(3, −4), ∆(P )=				18			0	=18 (−24)< 0 ,
2)	P	(3, −4), ∆(P )=				18			0	=18 (−24)< 0 ,
	2		2			0		−24
						0		−24
в точці P2 (3; −4)			відсутній екстремум;
3)	P	(−3, 4), ∆(P )=			−18 0					=(−18) 24 < 0 ,
3)	P	(−3, 4), ∆(P )=			−18 0					=(−18) 24 < 0 ,
	3		3		0				24
					0				24
в точці P3 (3; −4)			відсутній екстремум;
4)	P	(−3, −4), ∆(P )=					−18			0	=(−18) (−24)> 0, z′′2				(P )= −18	< 0 ,
4)	P	(−3, −4), ∆(P )=					−18			0	=(−18) (−24)> 0, z′′2				(P )= −18	< 0 ,
	4		4					0	−24					x	4
								0	−24

P4 (−3; −4) – точка максимуму.

Обчислимо значення екстремумів функції.

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
24.12.2018681.47 Кб7Metod G1.doc
#
24.12.2018416.26 Кб13Metod-G2.doc
#
04.02.20161.37 Mб48Metod-Z.pdf
#
04.02.2016291.33 Кб13Metodichka po English.doc
#
15.11.2019455.68 Кб7Metodichka.doc
#
04.02.2016515.54 Кб9Metodichka_dlya_zaochnik_2_sem (1).pdf
#
05.02.20161.15 Mб16Metodichni_vkazivki_1-3_lab_roboti.pdf
#
26.11.2018527.36 Кб2Metodichni_vkazivki_dlya_zaochnikiv_z_angl_movi....doc
#
04.02.2016872.79 Кб9metodichni_vkazivki_Excel.pdf
#
24.11.2019738.3 Кб3Metodichni_vkazivki_z_vikonannya_kursovoyi_robo...doc
#
05.02.2016781.32 Кб11MetodLabMOV.pdf