
МАТ_ ЛОГИКА / МАТЕМАТИЧЕСКАЯ ЛОГИКА_ЛК7+ЛК8_27_02_2012+05_03_2012_Теория предикатов первого порядка
.pdf"x(P*(x)ÞQ*(x))| = F. Из последнего следует, что существует такоех = а, что
|P*(a)ÞQ*(a)| = F, откуда |P*(a)| = T, |Q*(a)| = F. Тогда |"xQ*(x)| = F, и, возможно, существует такое b, что |P*(b)| = F, тогда |"xP*(x)| = F и |("xP*(x)Þ Þ"xQ*(x))| =
F. Следовательно, существует такая интерпретация, на которой формула принимает ложное значение.
12.5. Логическое следование в логике предикатов
12.5.1. Определение логического следования
ØОпределение 12.10. Говорят, что формула В логически следует из формулы A, если в любой интерпретации, в которой А принимает истинной значение, В также принимает истинное значение. Обозначение: А ╞ В.
В общем случае формулаВ является логическим следствием множества
формул Г, если она истинна на всех тех интерпретациях, на которых выполнены (истинны одновременно) все формулы из Г.
ØОпределение 12.11. Говорят, что формула A равносильна, или логически эквивалентна, формуле В, если каждая из них логически влечет другую, т.е. если A |= В и В |= A. Обозначение: AÛB
Из определений следуют утверждения:
1.A |= В тогда и только тогда, когда |= AÞВ.
2.A1,.., An |= В, тогда и только тогда, когда |= A1, &... & АnÞ В.
3.AÛB тогда и только тогда, когда |= AºB.
4.Если A|= В и |A| = Т, то |B| = T в некоторой интерпретации.
5.Если Г |= B и "i|Гi| = Г), то |B| = Г.
12.5.2.Основные правила вывода логики предикатов
Рассмотрим некоторые логические следования, которые выполнены в логике предикатов. Каждое такое логическое следование задает правило вывода в логике предикатов; некоторые из них будут использованы в формальной теории предикатов.
1. Правило универсальной конкретизации (УК):
"хА(х) |= А(у), если у свободно для х в А(х).
Доказательство. Нужно доказать, что если |"xA*(x)| = T в некоторой интерпретации D, то |A*(y)| = T в той же интерпретации. Допустим |A*(y)| = F. Тогда существует такое b Î D, что |A*(b)| = F.
Но по условию формула |"xA*(x)| = T на D, а так как b Î D то |"xA*(x)| = F на D. Это противоречие доказывает теорему.
2.Правило экзистенциальной конкретизации(ЭК):
$хА(х) |= А(b), где b Î D.
Доказательство. Допустим, |$хА*(х)| = T в некоторой интерпретацииD. Тогда существует такое b Î D что |A*(b)| = Т.
3.Правило экзистенциального обобщения:
А(у) |= $хА(х), где х свободно для у в А(у).
Доказательство. Если |A*(y)| = T в некоторой интерпретацииD то существует у = b, b Î D такое что |A*(b)| = Т. Следовательно, |$хA*(x)| = Т в интерпретации D.
4.Правило всеобщности:
СÞА(х) |= СÞ"х(A(х)), если С не содержит свободных вхождений х.
Доказательство. По условию |СÞА*(х)| = T в интерпретацииD. Это возможно, если
а) |
|С| = F, тогда |СÞА*(х)| = T и | СÞ"хА*(х)| = T; |
|
б) |
|С| = T, |СÞА*(х)| = T, следовательно, |А*(х)| = T |
в интерпретации D |
для любого х, значит |СÞ"хА*(х)| = T. |
|
|
5. |
Правило существования: A(х) ÞС |= |$хA(х) ÞС, |
если С не содержит |
свободных вхождений х. |
|
|
Доказательство. |А*(х)ÞС |=T в некоторой интерпретацииD. Допустим |
||
|$хA*(x) ÞС | = F в интерпретации D. Тогда |С| = F, (С не зависит от х) и |$хA*(x)| = Т, следовательно, существует x = b, такое что |А*(b)| = T и |А*(b)ÞС] = F, в то время как по условию|А*(b)ÞС] = Т. Полученное противоречие доказывает теорему.
6. Правило обобщенияGen (от английского словаGeneralization): если Г |= А(х), то Г |="хА(х), если х не входит свободно ни в одну из формул Г.
Доказательство. Предположим, выбрана область интерпретацииD и произведена замена в А всех свободных переменных на элементы из D, например, х=bÎD. Тогда |А*(b)| = T, так как |Гi| = T для всякого i. Так как х не входит свободно ни в одну из формулГ, то в множествеГ замены х на b не было ,и следовательно, для любого хÎD, такого что | А*(x)| = Т, Г|= А*(х), следовательно,
Г|="хА*(х).
12.6. Исчисление предикатов первого порядка
12.6.1. Формальная теория К
Поскольку построение таблиц истинности для любой формулы представляется возможным для проверки общезначимости формул теори предикатов, аксиоматический метод необходим для исследования формул, содержащих кванторы. Рассмотрим формальную теорию первого порядка К.
Символами |
теории К |
служат |
те |
же |
символы |
логики |
предикат: |
пропозициональные связки Þ, Ø, ", $, вспомогательные символы (, ), множества |
|||||||
предметных переменных: x1, |
x2, ..., |
предметных |
постоянных: a1, a2, |
..., |
|||
функциональные символы: fin, i = 1, ..., k, n = 0, ..., m, предикатные символы: Рin, i = 1, ..., k, n = 0, ..., m. Определения терма, формулы и пропозициональных связок &, Ú, º остаются в силе для теории первого порядка.
Аксиомы теории К разбиваются на логические аксиомы и собственные.
Логические аксиомы. Каковы бы ни были формулыА, В, С теории К, следующие формулы являются логическими аксиомами теории К.
A1 AÞ(BÞA)
A2 (AÞ(BÞC)) Þ((AÞB) Þ(AÞC)) A3 (ØBÞØA) Þ((ØBÞA) ÞB)
A4 "xA(x)ÞA(y), если у свободно для х в формуле А(х).
А5 "x(AÞВ(х))Þ (АÞ"xB(x)), если A не содержит свободных вхождений х.
Собственные аксиомы формулируются отдельно для каждой конкретной содержательной предметной области.
Правилами вывода во всякой теории первого порядка являются:
1.modus ponens (MP): из A и AÞВ следует В,
2.правило обобщения Gen: из Г|=А(х), следует Г|="хА(х), если х не входит свободно ни в одну из формул Г.
Теория К, не содержащая собственных аксиом, называется исчислением предикатов первого порядка.
Моделью теории первого порядкаК называется всякая интерпретация, в которой истинны все аксиомы теорииК. Если правила вывода МР Genи применяются к истинным в данной интерпретации формулам, то результатом являются формулы, также истинные в той же интерпретации. Следовательно, всякая теория К истинна во всякой ее модели.
Множество формул, выводимых по правилам вывода из аксиом теорииК, является теоремами теорииК. Аксиомы А1, А2, A3 теории К и правило МР определены в теорииL, следовательно, все теоремы теорииL включены в множество теорем теории К.
Метатеорема о дедукции в теорииК может быть сформулирована в ослабленном виде.
Метатеорема о дедукции. Если существует вывод формулыВ из множества гипотез Г и формулы А: Г, А |— В, и в этом выводе ни при каком применении правила Gen к формулам, зависящим от A, не связывается квантором никакая свободная переменная формулы А, то Г |— А Þ В.
Следствие 1. Если существует вывод Г,А|—В, и в этом выводе ни разу не применялось правило Gen к формулам, зависящим от А, то Г |— А Þ В.
Следствие 2. Если существует выводГ, А |— В, где А — замкнутая формула, то Г |— А Þ В.
12.6.2. Теория первого порядка с равенством
Рассмотрим теорию первого порядкаК, в числе предикатных символов которой содержится предикат равенстваA12(t, s), который для сокращения будем обозначать t = s, а вместо ØA12(t, s) соответственно будем писать t¹s.
ØОпределение 12.12. Теория К называется теорией первого порядка с равенством, если следующие формулы являются теоремами теории К:
А6. "x1(x1 = x2) |
(рефлексивностьравенства); |
А7. (х = у) Þ (А(х, х) Þ А(х, у)) (подстановочностъ равенства),
где х, у — предметные переменные, А(х, х) — произвольная формула, А(х, у) получается заменой каких-нибудь (не обязательно всех) свободных вхождений х на у, если у свободно для тех вхождений х, которые заменяются.
Докажем основные теоремы теории первого порядка с равенством.
Теорема 12.1. |— t = t для любого терма t.
Доказательство. Из А6: |— "x1(x1 = x2) по правилу универсальной конкретизации получаем |— t = t.
Теорема 12.2. |— х = у Þ у = х.
Доказательство. Пусть А(х, х) есть х = х, А(х, у) есть у = х. Тогда: |— (х = у) (х = х Þ у = х) согласно А7; |— х = х согласно теореме 12.1;
|— х = у Þ у = х по правилу удаления средней посылки.
Теорема 12.3. |— х = у Þ (у = z Þ х = z).
Доказательство. Пусть А(у, у) есть у = z, А(у, х) - х = z. Тогда, заменив х на у и у на х, получим:
|— (у = х) Þ (у = z —> х = z) согласно А7;
|—х = у Þ у = х согласно теореме 12.2; |—x=y Þ (y=z Þ x = z) по правилу силлогизма.
12.7. Доказательство логических следований в логике предикатов
12.7.1. Формализация предложений естественного языка
Язык логики предикатов традиционно служит для формализ высказываний естественного языка.
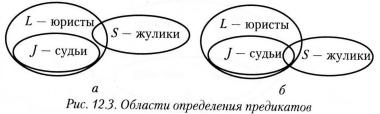
vПример. Рассмотрим область определения М = {люди} с заданными на ней предикатами:J(х): х — судья; L(x): x - юрист; S(x): х — жулик; А(х, у): х любит у.
Понятие «юрист» можно определить как множество всех людей, имеющих юридическое образование. Понятие «судья» можно определить как множество людей, имеющих юридическое образование, работающих в суде и выполняющих вполне определенные обязанности. Таким образом, множество судей является подмножеством множества юристов, т.е. свойство быть судьей влечет свойство быть юристом, и область истинности предикатаJ(x) включена в область истинности предиката L(x) (см. рис. 12.3), т.е. справедливо высказывание: каждый судья является юристом, что можно выразить в виде формулы: "x(J(x) —> L(x)).
Рассмотрим высказывание: «Некоторые юристы — жулики». Это высказывание истинно, если существуют такие объекты, которые являются одновременно и юристами, и жуликами: $x(L(x) & S(x)), т.е. области истинности предикатов L(x) и S(x) пересекаются: LÇS. Следует ли из этого, что существуют судьи-жулики? Нет, не следует.
Области истинности предикатов L(х) и S(x) могут пересекаться (рис. 12.3, б), а могут и не пересекаться(рис. 12.3, а). Мы могли бы сказать: «Возможно, существуют судьи-жулики», - однако категорию возможности нельзя выразить в теории предикатов 1-го порядка.
Формализуем некоторые другие высказывания:
$x(S(x) & "y(L(y) Þ А(х, у))) некоторые жулики любят всех юристов; $x(S(x) & "y(A(x,y) Þ L(y))) некоторые жулики любят только юристов; $x(S(x) & $y(L(y) & А(х, у))) некоторые жулики любят некоторых юристов;
"x(S(x) Þ "y(J(y) Þ ØA{х,у))) |
все жулики не любят судей. |
12.7.2. Основные схемы суждений |
|
В традиционной логике |
обычно выделяют четыре основных схе |
суждений.
1). Общеутвердительное суждение: А: Все S суть P: "x(S(x) Þ Р(х)).
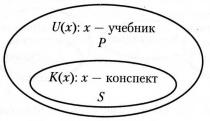
v Пример. В последующих примерах пустьx Î {люди}, у Î {произведения}. На этих областях заданы предикаты: Р(х): х - писатель, V(x): х - поэт, W(x, у): х пишет у, N(y):y - роман, К(у):у - конспект, С(у): y - стихи, U(y): у - учебник. Рассмотрим два понятия: «учебники» и «конспекты». Понятие «учебники» обладает тем свойством, что это книги, по которым учатся. Предикат U(x) среди всех книг выделяет , текоторые являются учебниками. По конспектам также учатся, однако, конспекты обладают еще и тем свойством, что они написаны от руки. Поэтому конспекты можно считать подмножеством учебников(см. рис. 12.4). Отсюда следует, что «каждый конспект является учебником», или «все конспекты — учебники», что выражается формулой: "х(К(х) Þ U(x)).
Рис. 12.4. "х(К(х) Þ U(x)) - Все конспекты – учебники
2). Общеотрицательное суждение: Е: Ни одно S не суть Р: "х(S(х) Þ
ØP(x)).
v Пример. Рассмотрим два понятия: «конспекты» и «романы». Очевидно, что области истинности этих предикатов не пересекаются(см. рис. 12.5), т.е. «ни один конспект не является романом», что выражается формулой:
"х(K(х) Þ ØN(x))
.
Рис. 12.5. "х(K(х) Þ ØN(x)) - Ни один конспект не является романом
3). Частноутвердительное суждение: I: Некоторые S суть Р - $x(S(x) & P(x))
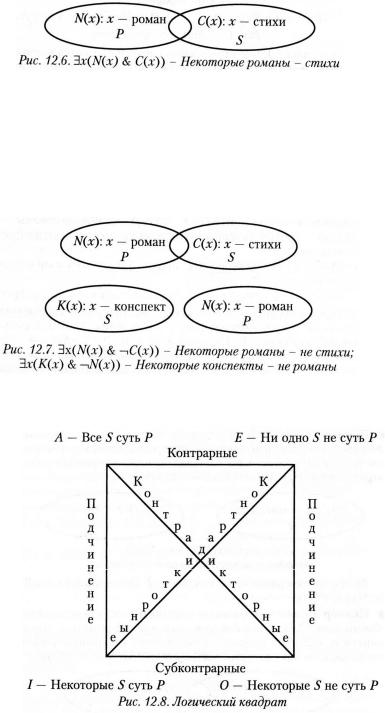
v Пример. Понятия «романы» и «стихи» имеют пересекающиеся объемы (рис. 12.6), - как известно, существуют романы в стихах, например, «Евгений Онегин». Утверждение «некоторые романы написаны в стихах» выражается формулой: $x(N(x) & C(x)).
4). Частноотрицательное суждение: О: Некоторые S не суть Р: $x(S(x) &
ØP(x)).
v Пример. Рассмотрим утверждения: «некоторые романы – не стихи»: $x(N(x) & ØC(x)), «некоторые конспекты - не романы»: $x(K(x) & ØN(x)). Области истинности соответствующих предикатов могут пересекаться, могут и не пересекаться (см. рис. 12.7).
Эти четыре типа суждений образуют так называемыйлогический квадрат, который показывает связь между схемами суждений (рис. 12.8).
Суждения, соединенные диагоналями, называются контрадикторными. Контрадикторные утверждения несовместимы по истинности и несовместимы по
ложности, т.е. не |
могут быть одновременно истинными, |
не |
могут |
быть |
одновременно ложными. Одно является отрицанием другого: |
|
|
|
|
1) ØА = О, |
т.е. «не все S суть Р» º «некоторые |
S не |
суть |
».Р |
Действительно: "x(S(x) Þ Р(х)) º $x(ØS(x) Ú P(x)) º $x(S(x) & ØP(x)). Например,
"x(N(x) Þ С(х)) («все |
романы |
написаны в стихах» |
$x(N(x) & ØC(x)) |
(«некоторые романы — |
не стихи») |
— контрадикторные |
утверждения, одно |
является отрицанием другого. |
|
|
|
2) ØE=I, т.е. «неверно, что ни одно S не суть Р» º «некоторые S суть Р».
Ø"x(S(x) Þ ØР(x)) º $xØ(ØS(x) Ú ØР(х)) º $x (S(x) & Р(х)).
Горизонтальные стороны квадрата показывают отношения контрарности и субконтрарности. Утверждения А: Все S суть Р: "x(S(x) Þ Р(x)) и Е: Ни одно S не суть Р: "x(S(x) Þ ØР(x)) называются контрарными. Они совместимы по ложности, но несовместимы по истинности, .е. могут быть одновременно ложными, но не могут быть одновременно истинными. Например, «все романы написаны в стихах»: "x(N(x) Þ С(х)) и «ни один роман не написан в стихах»: "x(N(x) Þ ØС(х)), — контрарные утверждения; оба они ложны. Утверждения: «все люди смертны» и «все люди бессмертны», — также контрарны, первое — истинно, второе ложно.
Утверждения I: Некоторые S суть P: $x(S(x) & Р(х)) и О: Некоторые S не суть Р: $x(S(x) & ØP(x)) называются субконтрарными. Субконтрарные утверждения совместимы по истинности, но несовместимы по ложности, т.е. могут быть одновременно истинными, но не могут быть одновременно ложными. Например, «некоторые романы - стихи»: $x(N(x) & C(x)) и «некоторые романы не стихи»: $x(N(x) & ØС(х)), - субконтрарны; оба они истинны.
Вертикальные стороны квадраты показывают отношение логического
следования (в |
логическом квадрате— |
отношение |
подчинения): утверждения, |
||||
находящиеся |
снизу, логически |
следуют |
из |
, техчто |
находятся |
сверху. |
|
Действительно, если «все S суть Р», то |
и «некоторые S суть Р», т.е. выполнено |
||||||
логическое следование: "x(S(x) Þ Р(x)) |= $x(S(x) & Р(х)), откуда следует, что |А
Þ I| º Т. Например, если «все |
конспекты — учебники», то |
и «некоторые |
конспекты — учебники». Другое |
логическое следование также |
очевидно: если |
«ни одно S не суть Р», то и «некоторые S не суть Р»: "x(S(x) Þ ØР(x)) |= $x(S(x) & ØР(х)), откуда следует, что |E Þ O| º Т. Например, если «ни один учебник не написан в стихах», то и «некоторые учебники не написаны в стихах».
Другие примеры формализации высказываний приведены в таблице 12.6.
Таблица 12.6
Все конспекты - учебники. |
"y(K(y) Þ U(y)) |
|
|
|
|
Конспект |
по математике(М) — |
K(M) Þ U(M) |
учебник. |
|
|
|
|
|
Ни один |
учебник не написан |
в |
стихах. |
|
"y(U(y) Þ ØC(y)) |
|
|
|

Некоторые |
романы |
написаны |
в |
стихах. |
|
|
$y(N(y) & C(y)) |
|
|
|
|
«Евгений |
Онегин» - |
это роман |
в N(Е. Онегин) & C(Е. Онегин) |
стихах. |
|
|
|
Все поэты пишут стихи. |
|
"x(V(x) Þ "y(C(x) Þ W(x, y)) |
|
|
|
|
|
Некоторые |
писатели |
пишут только |
$x(P(x) & "y(W(x, y) Þ N(y))) |
романы. |
|
|
|
Писатель Лев Толстой писал только |
P(Толстой) & "y(W(Толстой, y) Þ |
||
романы. |
|
|
N(y)) |
Каждый что-нибудь пишет. |
"x$yW(x, y) |
||
|
|
||
Каждый, кто пишет что-нибудь, пишет |
"x($yW(x, y) Þ W(x, NY)) |
||
поздравление с Новым годом (NY). |
|
||
Некоторые люди ничего не пишут. |
$x"yØW(x, y) |
||
|
|
|
|
12.7.3. Доказательство логических следований
В данном разделе мы рассмотрим два способа доказательства логических следований: неформальный способ, основанный на доказательстве от противного, и формальный вывод в исчислении предикатов. В следующий главе будет рассмотрен более эффективный метод, позволяющий автоматизировать процесс поиска доказательства логического следования (логической общезначимости).
v Пример 12.1. На области определения «люди» заданы высказывания: 1)Некоторые студенты любят своих преподавателей.
2)Никто не любит невежественных людей.
Следовательно, ни один преподаватель не является невежественным. Пусть Р(х): х — студент, D(x): x — преподаватель, Q(x): x — невежественный, L(x, у): х любит у. Формализуем посылки:
Fl: $x(P(x) & "y(D(y) Þ L(x,y))), F2: "x(P(x) Þ "y(Q(y) Þ ØL(x,y))).
Заключение G: "y(D(y) Þ ØQ(y)).
По определению, |F1| = T, |F2| = Т. Предположим, что |G| = F. Из предположения |"y(D(y) Þ ØQ(y))| = F следует, что существует по крайней мере одно значение у = а, такое что |D(a) Þ ØQ(a)| = F, откуда получаем, что |D(a) = Т, |ØQ(a)| = F, т.е. |Q(a)| = Т. Из посылки F1: |$х(Р(х) & "y(D(y) Þ L(х, y)))| = Г
следует, что существует по крайней мере одно значениех = b, такое, что P(b) &
"y(D(y) Þ L(х, y))| = Т, откуда получаем: |Р(b)| = Т и |"y(D(y) Þ L(х, y))| = Т.
Поскольку последнее истинно для всякогоу, в том числе, для у = а, получаем
|(D(a) Þ L(b, a))|= = T, т.е. |(T Þ L(b, а))| = Т, откуда |L(b, a)| = Т.
Поскольку посылка F2: |"х(Р(х) Þ "y(Q(a) Þ ØL(x, a)))| = T для всех значений х и у, то она истинна и для х = b, у = а: |P(b) Þ (Q(a) Þ ØL(x, a))| = Т. А
поскольку |Р(b)| = Т, то |Q(a) Þ ÞØL(b, a))| = Т. Так как |Q(a)| = T, то |ØL(b, a)| =
Т. Получаем, что истинны оба утверждения: |L(b, а)| = T и |ØL(b, a)| = Т. Полученное противоречие доказывает логическое следование. В формальном выводе применяются правила: универсальной конкретизации (УК), экзистенциальной конкретизации (ЭК), удаления & (уд. &), введения & (вв. &), правило МР.
|
Формальный вывод. |
|
1. |
$х(Р(х) & "y(D(y) Þ L(x, у))) |
Г1 |
2. |
"x(P(x) Þ "y(Q(y) Þ ØL(х, у))) |
Г2 |
3. |
P(b) & "y(D(y) Þ L(b, у)) |
ЭК(1) |
4. |
P(b) |
уд. &(3) |
5. |
"y(D(y) Þ L(b, у)) |
уд. &(3) |
6. |
P(b) Þ "y(Q(y) Þ ØL(b, у)) |
УК(2) |
7. |
"y(Q(y) Þ ØL(b,y)) |
МР(4, 6) |
8. |
Q(z) Þ ØL(b, z)) |
УК(7) |
9. |
D(z) Þ L(b, z)) |
УК(5) |
10.L(b, z) Þ ØQ(z) |
правило контрапозиции (8) |
|
11.D(z) Þ ØQ(z) |
правило силлогизма (9, 10) |
|
12."y(D(y) Þ ØQ(y)) |
Gen(11) |
|
vПример 12.2. На области определения «люди» заданы высказывания:
1.Все старые члены конгресса — юристы.
2.Все женщины-юристы восхищаются каким-нибудь судьей.
3.Только судьи восхищаются судьями.
4.Все судьи восхищаются всеми судьями.
Что думает судья Джонс по поводу своей старой тещи, которая является членом конгресса? Ответ. Джонс восхищается своей тещей. Проверить, что это заключение логически следует из заданных посылок.
Пусть х — предметная переменная, которая принимает значения из области определения «люди». Введем предикаты:J(х):х — судья; L(x): х — юрист; С(х): х
— член конгресса; W(x): x — женщина; А(х, у): х восхищается у, D - Джонс, Т - теща. Формализуем посылки.
1."х(О(х) & С(х) Þ L(x))
Все старые члены конгресса — юристы.
2."x(W(x) & L(x) Þ $y(J(y) & А(х,у)))
Все женщины-юристы восхищаются каким-нибудь судьей.
3."x"y(J(y) & A(x,y) Þ J(x))
Только судьи восхищаются судьями.
4."x(J(x) Þ "y(J(y) Þ А(х,у)))
Все судьи восхищаются всеми судьями.
5.J(D) Джонс – судья.
6.W(T) & О(Т) & С(Т) старая теща, член конгресса.
Доказать: A(D, Т) - судья Джонс восхищается тещей.
Формальный вывод.
1. |
"x(O(x) & С(х) Þ L(x)) |
Г1 |
2. |
"x(W(x) & L(x) Þ "y(J(y) & А(х, у))) |
Г2 |
3. |
"x"y(J(y) & А(х, у) Þ J(х)) |
ГЗ |
4. |
"x(J(x) Þ "y(J(y) Þ A(x, у))) |
Г4 |
5. |
W(T) & O(T) & C(T) |
Г5 |
6. |
J(D) |
Г6 |
7. |
J(D) Þ "y(J(y) Þ A(D,у)) |
УК (4) |
8. |
"y(J(y) Þ A(D, y)) |
MP(6,7) |
9. |
J(T) Þ A(D, T) |
УК (8) |
10.O(T) & C(T) Þ L(T) |
УК(1) |
|
11.O(T)&С(T) |
уд. &(5) |
|
12.L(T) |
МР (11,10) |
|
13.L(T) Þ $у(J(у) & А(Т, у)) |
УК (2) |
|
14.W(T) |
уд. &(5) |
|
15.W(T) & L(T) |
вв. & (12,14) |
|
16.$y(J(y)&A(T,y)) |
МР(13,15) |
|
17.J(a)& A(T, a) |
ЭК (16) |
|
18.J(a)& A(T, а) Þ J(T) |
УК(3) |
|
19.J(T) |
MP(18, 17) |
|
20.A(D, T) |
МР(9, 19) |
|
