
Методы оптимизации учебник
.pdf
НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Результаты всех вычислений приведены в таблице, из которой следует, что значение функции f (x) становится меньше ε = 0,1на 11-й итерации, а значение нормы градиен-
та уменьшается в 5/6 раза каждые две итерации.
Скорость сходимости метода Коши является довольно низкой, хотя на каждой итерации обеспечивается выполнение неравенства f (xk +1 ) ≤ f (xk ) .
k |
|
|
|
|
|
xk |
|
|
|
|
f (x) |
f (xk ) |
|
|
|
f (xk ) |
|
|
|
|
λk |
|
|
xk +1 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
1 |
|
|
|
|
|
|
|
; |
1 |
|
|
6/10 |
(-2;0) |
2 |
|
|
|
|
0,05 |
|
(-0,5;1) |
|||||||||||||||
|
|
− 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
10 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 |
|
−5 |
|
|
|
|
|
5/10 |
(0;1) |
1 |
|
|
|
1/6 |
(-1/2;5/6) |
|||||||||||||||||||||
|
|
10 |
|
;1 |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3 |
|
− |
|
1 |
; |
|
5 |
|
|
5/12 |
(-5/3;0) |
5/3 |
|
|
|
0,05 |
|
|
(- |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
2 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
5/12;5/6) |
|||||||||||||||
4 |
|
− |
|
5 |
|
; |
5 |
|
|
25/72 |
(0;5/6) |
5/6 |
|
|
|
1/6 |
|
|
− 5 |
; |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
|||||||||||
|
|
|
|
12 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
36 |
|||||||||||||
5 |
|
|
|
5 |
; |
|
|
|
|
|
|
|
125/432 |
(-25/18;0) |
25/18 |
|
|
|
0,05 |
|
|
|
|
; |
25 |
|
|
|||||||||
|
|
− |
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
− 25 |
|
|
|
||||||||||||||
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
72 |
|
|
36 |
|||||||||||||||
6 |
|
|
|
|
|
|
; |
|
|
|
|
|
625/2592 |
(0;25/36) |
25/36 |
|
|
|
1/6 |
|
|
; |
|
|
|
|
|
|||||||||
|
|
− |
25 |
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
− 25 |
|
|
125 |
|||||||||||||
|
|
72 |
|
|
|
36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
72 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
216 |
|||||||||||||||||
7 |
|
|
|
|
|
; |
|
|
|
|
|
|
|
5 |
|
(125/108;0) |
125/108 |
0,05 |
|
−125 |
; |
|
|
|
|
|
|
|||||||||
|
|
− |
25 |
|
|
125 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
125 |
|||||||||||||||
|
|
72 |
|
|
216 |
|
265 |
|
|
|
|
|
|
|
|
|
|
|
432 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
216 |
|||||||||||||||||||
……………………………………………………………………………
11 |
|
− 5 |
|
; |
5 |
|
|
5 |
9 |
9 ≈ 0,1 |
5 |
5 |
4 ≈ 0,16 |
|
|
|
|
|
4 |
|
|
5 |
|
|
|
… |
|
||
|
|
|
|
|
|
|
|
|
26 |
|
36 |
|
||
|
26 |
4 |
|
6 |
5 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ 10
Решить задачу безусловной оптимизации методом Коши с точностью ε=0,1. Решение сопроводить геометрической интерпретацией.
1. − x1 +6x2 −2x12 −3x22 +3x1x2 → max
2.6x1 + 4x2 − x12 − 12 x22 − x1x2 → max
3.6x1 + 4x2 − x12 − 12 x22 − x1x2 → max
4.6x1 + 4x2 − x12 − 12 x22 − x1x2 → max
5.3x1 −2x2 − 12 x12 − x22 + x1x2 → max
6.3x1 −2x2 − 12 x12 − x22 + x1x22 → max
7.−4x1 +8x2 − µx12 − 32 x22 + 2x1x2 → max
91

НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
|
8. |
|
−4x |
|
+8x |
2 |
− x2 |
− |
3 |
x2 + 2x x |
2 |
→ max |
|
|||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
1 |
|
2 |
|
2 |
|
1 |
|
|
|
|
|
|
|
|||||||||
|
9. |
|
6x |
2 |
|
− x2 |
− |
3 |
x2 |
+ 2x x |
2 |
→ max |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
2 |
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
10. |
6x |
2 |
|
−2x |
2 − |
7 |
x2 |
+ 2x x |
2 |
→ max |
|
||||||||||||||||||||
|
|
2 |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Методы условной оптимизации |
|
||||||||||||||||
|
|
|
|
|
|
|
|
Постановка задачи. Классификация методов. |
|
|||||||||||||||||||||||
|
Рассмотрим следующую задачу: |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ( |
|
) → max |
(4.3.1) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|||||||||||
на множестве P: |
|
|
|
|
|
P = {x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
} |
|
|||||||
|
|
|
|
|
|
|
|
|
E n |
: gi ( |
|
|
|
|
|
(4.3.2) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
) ≤ 0, i =1, m |
, x j ≥ 0, j =1, n |
|||||||||||||||||||||
где |
f ( |
|
) и gi ( |
|
) - нелинейные функции. |
|
|
|
|
|
|
|||||||||||||||||||||
x |
x |
|
|
|
|
|
|
|||||||||||||||||||||||||
При решении задач нелинейного программирования ввиду нелинейности функции gi (x ) выпуклость допустимого множества решений P и конечность числа его крайних точек (в отличие от ЗЛП) необязательны. Задача нелинейного программирования не всегда
имеет решение. Если задача имеет решение, то максимум функции f (x ) может дости-
гаться в крайней точке допустимой области значений P, в одной из граничных точек или в точке, расположенной внутри допустимой области P.
Определение 4.3.1.1. Решением или точкой максимума задачи условной оптимизации называется такой вектор x * P E n , что f (x * ) ≥ f (x ) для всех x P , т.е.
f (x * ) = max f (x ) .
x P
Определение 4.3.1.2. Направление S ≠ 0 называется возможным в точке x P , ес-
ли существует |
такое действительное |
число β0 > 0 , что ( |
x |
k + β |
S |
) P для всех |
||||||||||||||||
β (0, β0 ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Определение 4.3.1.3. Вектор |
|
k |
называется возможным направлением подъема |
|||||||||||||||||||
S |
||||||||||||||||||||||
функции f ( |
|
) |
в точке |
|
|
k P , если существует такое действительное число β0 > 0 , что |
||||||||||||||||
x |
X |
|||||||||||||||||||||
для всех β (0, β0 ) : |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
( |
|
k + β |
|
k ) P и f ( |
|
k + β |
|
k ) > f ( |
|
k ) . |
||||||||
|
|
|
|
x |
S |
x |
S |
x |
||||||||||||||
Методы решения задачи условной оптимизации можно представить как итераци- |
||||||||||||||||||||||
онный процесс, в котором исходя из начальной точки x 0 P , получают последовательность точек x k P , монотонно увеличивающих значения функции f (x ) . Это так называемые методы подъема. Элементы этой последовательности точек определяются следующим образом: x k +1 = x k + βk S k ,
92
|
|
|
|
|
|
|
|
|
|
|
НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
|
|
|
- возможное направление подъема функции в точке |
|
k . |
|||||||||
|
S |
k |
x |
||||||||||||
|
|
|
βk |
находится при решении задачи одномерной оптимизации: |
|||||||||||
|
|
|
|
|
|
|
|
|
|
) → max . Если точка |
|
k - внутренняя точка множества P, т.е. для |
|||
|
|
|
f ( |
|
|
k + β |
|
k |
x |
||||||
|
|
|
x |
S |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
β |
||||
|
|
|
|
|
|
||||||||||
i =1, m |
: gi (x k ) < 0 , |
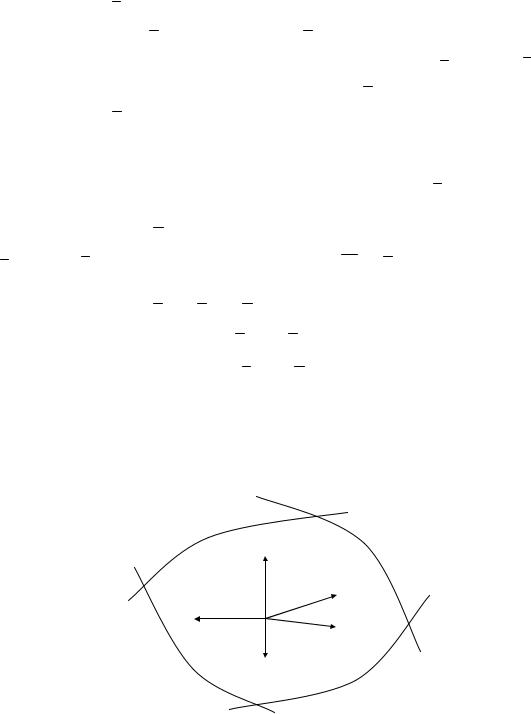
то всякое направление в ней является возможным (пример на рис. |
|||||||||||||
4.3.1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
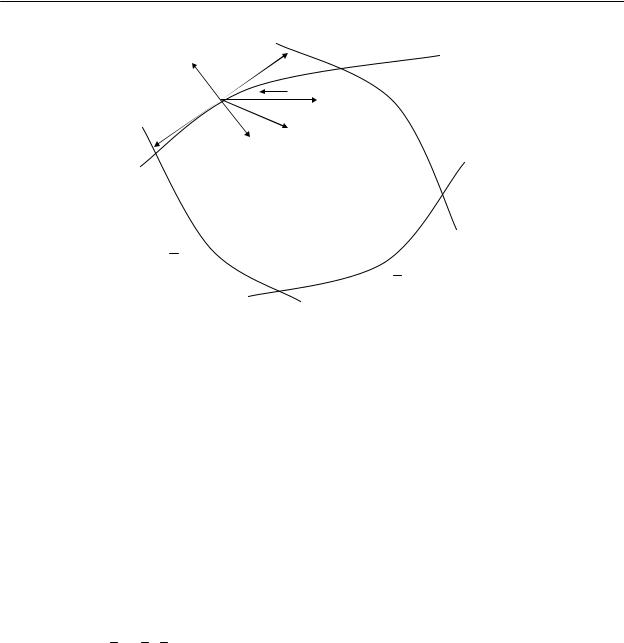
Если точка x k - граничная точка области P, то возможные направления определяются ограничениями gi (x k ) = 0 (направление S * на рис. 4.3.2. возможным не является).
Прежде чем определять направление подъема функции f (x ) в точке x k , следует вычислить множество таких возможных направлений S k , для которых существовала бы
окрестность точки x k , принадлежащая P.
Общая схема методов условной оптимизации
Начальный этап. Задать ε > 0 и выбрать начальную точку x0 P . Основной этап.
Шаг 1. Выбрать S k (k-я итерация) - возможное направление подъема функции
f (x ) в точке x k . Если такого направления нет, то x* k =x k - решение задачи. В противном случае перейти к шагу 2.
Шаг 2. Положить x k+1 =x k +βS k , где βk находим, решая задачу
f (x k + βk S k ) → max
β>0
(x k + βk S k ) P
Шаг 3. Заменить k на k+1 и перейти к шагу 1.
Конкретные методы условной оптимизации различаются способом выбора воз-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
можного направления подъема S k функции |
f ( |
x |
) в точке x k . |
|||||||||||||
g1 ( |
|
) = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
g2 (x ) = 0 |
|||||||
|
|
P |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||
|
|
… |
|
|
|
|
|
S |
||||||||
|
|
xk |
|
|
|
|
||||||||||
|
S 4 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
S |
||||||||
|
|
|
S |
3 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
g4 |
( |
x |
) = 0 |
|
|
|
|
|
g3 |
(x ) = 0 |
|||||||
|
|
|
|
|||||
|
|
|
|
Рис. 4.3.1. |
|
|
|
|
93
НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
|
|
|
|
g1 ( |
x |
) = 0 |
|
|
S * |
|
|
||||||
|
|
|
|
|
||||
|
|
x |
|
|
|
g2 ( |
|
) = 0 |
|
|
k |
|
|
x |
|||
P
g4 (x ) = 0
g3 (x ) = 0
Рис 4.3.2 |
|
|
|
|
|
|
|
||||||||||||||
Метод Зойтендейка |
|
|
|
|
|
|
|
||||||||||||||
Пусть требуется найти максимальное значение вогнутой функции |
f ( |
|
) : |
|
|
|
|
||||||||||||||
x |
|||||||||||||||||||||
f ( |
|
) → max |
|
|
|
|
|
|
|
||||||||||||
x |
|
|
|
|
|
|
|
||||||||||||||
при условиях |
|
|
|
|
|
|
|
||||||||||||||
|
|
A |
|
≤ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
x |
b |
|
|
|
|
|
|
|
|||||||||||
P = |
|
|
|
|
|
|
|
|
|
|
(4.3.2.1) |
||||||||||
|
|
x ≥ 0 |
|
|
|
|
|
|
|
||||||||||||
Характерной особенностью этой задачи является то, что ее система ограничений |
|||||||||||||||||||||
содержит только линейные неравенства. |
|
|
|
|
|
|
|
||||||||||||||
Предположим также для любой допустимой точки X, что A1 |
x |
= |
b |
1 |
и A2 |
x |
< |
b |
2 , где |
||||||||||||
A = ( A1, A2 ) и b = (b1,b2 ) . Далее приводится алгоритм метода Зойтендейка для случая линейных ограничений.
|
|
|
Алгоритм метода Зойтендейка |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Начальный этап. Выбрать начальную точку x 0 |
|
|
P , для которой |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
A =(A1, A2 ), |
|
=( |
|
|
1, |
|
|
2 ), |
|
||||||||||||||||
|
|
|
b |
b |
b |
||||||||||||||||||||||||||||
|
|
|
|
|
|
A1 : A1 |
|
0 = |
|
1, A2 : A2 |
|
0 < |
|
2 . |
|||||||||||||||||||
|
|
|
x |
b |
x |
b |
|||||||||||||||||||||||||||
Положить k=0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Основной этап. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Шаг 1. Для |
|
k |
P предполагаем, что A =(Ak ,Ak ), |
||||||||||||||||||||||||||||||
x |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
=( |
|
1k , |
|
2k ),A |
|
k = |
|
1,A |
|
k < |
|
2 . |
||||||||||||||||
|
|
|
b |
b |
b |
x |
b |
x |
b |
||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
94

НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Шаг 2. Определить возможное направление подъема , решая следующую задачу:
ϕ( |
S |
) =( f ( |
x |
k ), |
S |
) →max |
(4.3.2.2) |
|||||||
при условиях: |
|
|||||||||||||
Pk ={S |
: |
|
En ,A1 |
|
|
≤0, |
(4.3.2.3) |
|||||||
S |
S |
|||||||||||||
|
|
−1≤S j ≤1, j = |
|
} |
|
|||||||||
|
|
1,n |
|
|||||||||||
Шаг 3. Если все ϕ(S ) =( f (x k ),S k ) =0, то x * = x k - задача решена.
Шаг 4. Определить βk (шаг в направлении S k ), решая задачу одномерной оптимизации:
f (x k + βS k ) → max 0 ≤ β ≤ β* .
Шаг 5. Положить x k +1 = x k + βk S k , заменить k на k+1 и перейти к шагу 1.
Пример.
f (x) = 4x1 + 6x2 + 2x1 x2 − 2x12 − 2x2 2 → max
x1 + x2 ≤ 2x1 +5x2 ≤ 5− x1 ≤ 0
− x2 ≤ 0
Начальный этап.
Выбираем начальную точку x0 = (0,0) , для которой:
A0 |
−1 |
0 |
|
|
|
|
0 |
|
1 |
1 |
|
|
|
2 |
||||
|
|
|
|
|
|
|||||||||||||
= |
|
,b 0 |
= |
|
, A0 |
= |
|
,b 0 |
= |
|
. |
|||||||
1 |
|
0 |
|
1 |
|
0 |
|
2 |
|
5 |
|
2 |
|
5 |
|
|||
|
|
−1 |
|
|
|
|
|
1 |
|
|
|
|
|
|||||
f (x) = (4 + 2x2 |
− 4x1 ,6 + 2x1 − 4x2 ) , положить k=0. |
|||||||||||||||||
Основной этап.
Итерация 1.
Шаг 1. Для x0 = (0,0) заданы A10 ,b10 , A20 ,b20 .
Шаг 2. f (x0 ) = (4,6) .
Решаем задачу
ϕ(S) =( f (x0 ),S) =4S1 +6S2 →max
при условиях
− S1 ≤ 0
− S2 ≤ 0
−1 ≤ S1 ≤1
−1 ≤ S2 ≤1
При решении этой задачи симплекс-методом получаем S0 = (1,1),ϕ(S0 ) =10 .
95

НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Шаг 3. Так как ϕ(S0 ) =10 ≠ 0 , переходим к шагу 4. Шаг 4. Решаем одномерную задачу:
f (x0 + βS 0 ) =10 − 2β 2 → max
0≤β≤β*
Определяем β* :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
* |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= min |
|
|
|
|
, |
|
|
|
|
|
= |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
т.е. решаем задачу: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 − 2β* |
|
→ max |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 ≤ β ≤ |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Очевидно, что решением является β0 |
= |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Шаг 5. Положить |
|
|
|
1 |
= |
|
|
0 |
+ β0 |
|
0 |
= (0,0) + |
|
5 |
(1,1) = ( |
5 |
, |
5 |
) . |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
x |
x |
S |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
6 |
|
|
|
6 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
k=1 и перейти к шагу 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Итерация 2. |
|
5 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Шаг 1. Для |
|
|
1 |
= ( |
, |
|
) : A |
= (1 |
|
5) |
|
|
|
|
|
|
|
11 |
|
= (0) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
x |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
6 |
|
|
|
|
6 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Шаг 2. f ( |
|
1 ) = ( |
7 |
, |
|
|
13 |
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Решаем задачу |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
1 |
+ |
|
S |
2 |
|
|
→ max |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
при условиях |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S1 +5S 2 |
|
≤ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 ≤ S1 |
≤1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 ≤ S 2 |
|
≤1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Оптимальное решение этой ЗЛП - |
|
|
1 |
= (1, − |
1 |
); |
|
ϕ |
( |
|
|
|
1 ) = − |
22 |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
S |
S |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
15 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Шаг 3. Так как |
|
ϕ( |
|
|
1 ) = − |
|
|
≠ 0 , переходим к шагу 4. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
S |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Шаг 4. Решаем задачу линейного поиска: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
f ( |
|
1 + β |
|
1 ) = |
125 |
+ |
22 |
|
β − |
62 |
|
β2 |
→ max |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
S |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
8 |
|
|
15 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
β* : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
0≤β≤β* |
||||||||||||||||||||||||||
Определяем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
* |
= min |
1/ 3 |
|
, |
|
5 / 6 |
|
= |
|
5 |
|
/ |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1/ 5 |
12 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
Таким образом, решая задачу |
|
|
|
|
|
|
|
|
4 / 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
125 |
|
+ |
22 |
β − 62 |
|
β2 → max , |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
15 |
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0≤β ≤ |
|
|
5 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
96
НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
получим оптимальное значение β : β1 =18655 .
Шаг 5. Положить:
x 2 = x1 + β1S 1 = ( 3531, 2431) . K=2 и перейти к шагу 1.
Итерация 3. |
= ( 35 , |
24 ) : A2 |
|
|
|
|
|
|
|
|||||||||||
Шаг 1. Для |
|
|
2 |
= (1 |
5) |
|
|
12 = (0). |
||||||||||||
x |
|
b |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
31 |
|
31 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Шаг 2. f ( |
|
2 ) = ( |
32 |
, |
160 ) |
|
|
|
|
|
|
|
|
|||||||
x |
|
|
|
|
|
|
|
|
||||||||||||
Решаем задачу |
31 |
|
31 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
32 S |
|
|
160 S |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
+ |
2 |
→ max |
||||
при условиях |
|
|
|
|
|
|
31 |
|
|
31 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
S1 +5S2 |
|
≤ 0 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 ≤ S1 ≤1 |
||||
Решение: |
|
|
|
|
|
|
|
|
|
−1 ≤ S2 |
≤1. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
2 = (1; − 1 ). |
ϕ( |
|
2 ) = 0 . |
|
|
|
|
|
|
|
|
|||||||
|
S |
S |
|
|
|
|
|
|
|
|
||||||||||
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Шаг 3. Так как ϕ(S 2 ) = 0 , задача решена и x * = x 3 = (3531, 2431).
На рис. 4.3.3. проиллюстрирован процесс решения задачи.
x 2
1,0 |
g2 (x ) = 0 |
x 3
x 2
g1 (x ) = 0
x1 0 |
2,0 |
x1 |
Рис. 4.3.3
97
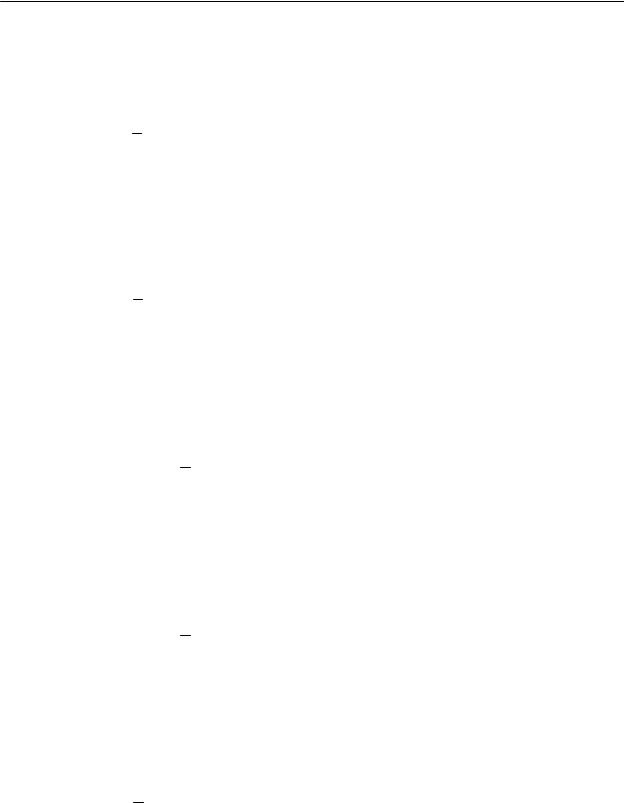
НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
ЗАДАНИЕ 11
Решить задачу нелинейного программирования методом Зойтендейка. Решение проверить графически.
1.
3x1 − 2x2 − 12 x12 2x1 + x2 ≤ 2
x1 + 2x2 ≤ 2 x1, x2 ≥ 0
2.
3x1 − 2x2 − 12 x12 x1 ≤ 3
x2 ≤ 6
x1, x2 ≥ 0
3.
− 4x1 + 8x2 − x12
x1 + x2 ≤ 3 x1 − x2 ≤1 x1, x2 ≥ 0
4.
−4x1 + 8x2 − x12
−x1 + x2 ≤1
x1 ≤ 4
x1, x2 ≥ 0
5.
3x1 − 2x2 − 12 x12 − x1 + 2x2 ≤ 2
2x1 − x2 ≤ 2 x1, x2 ≥ 0
−x22 + x1x2 → max
−x22 + x1x2 → max
−32 x22 + 2x1x2 → max
−32 x22 + 2x1x2 → max
−x22 + x1x2 → max
98

НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
6.
− x1 + 6x2 − x12 − 3x22 − 3x1x2 → max x1 − x2 ≥ 0
x2 ≤ 5
x1, x2 ≥ 0
7.
6x1 − x2 − 23 x22 + 2x1x2 → max − x1 + 2x2 ≤ 2
x1 ≤ 4 x1, x2 ≥ 0
8.
6x1 + 4x2 − x12 − 12 x22 − x1x2 → max 2x1 + x2 ≤ 2
x2 ≤1
x1, x2 ≥ 0
9.
6x1 + 4x2 − x12 − 12 x22 − x1x2 → max 3x1 + 2x2 ≤ 6
3x1 + x2 ≥ 3 x1, x2 ≥ 0
99

Ирина Николаевна Мастяева Ольга Николаевна Семенихина
МЕТОДЫ ОПТИМИЗАЦИИ
Учебно-методический комплекс
Ответственный за выпуск А.И.Комаров
Редактор Н.А.Соколова
Компьютерная верстка И.Ю.Ефремова
Издательский центр Евразийского открытого института 119501, г. Москва, ул. Нежинская, д. 13.
Тел.: (495) 442-23-92
Подписано в печать 07.09.08. Формат 60 × 84 1/8. Бумага офсетная. Печать офсетная.
Печ. л. 12,5. Тираж 50 экз.
Отпечатано в ООО «Футурис».
127051, г. Москва, Каретный Б. пер., д. 24/12, кор. стр. 1.
Тел.: (495) 772-31-07
