chirskii-lectures-2sem

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Российская академия народного хозяйства и государственной службы при Президенте Российской Федерации

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Если z(x, y) дифференцируема в точке (x0 , y0 ), то положим в (2)

и заметим, что:

.pdf

Скачиваний:

Добавлен:

08.04.2015

Размер:

1.57 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 119 10 11 > Следующая >>>

Математический анализ I курс II семестр

Билет 23. Касательная плоскость (стр. 1 из 1)

Билет 23. Касательная плоскость.

Пусть z z(x, y) дифференцируема в точке (x0 , y0 ). Докажем, что существует касательная плоскость к этой поверхности в точке (x0 , y0 ) и что она задается уравнением:

z z ( x0 , y0 )	z	( x0 , y0 )( x	x0 )	z	( x0 , y0 )( y	y0 )	1
	x			y

По аналогии с одномерным случаем (прямая называется касательной к кривой в точке x0 ,

если расстояние от точки M до этой прямой представляет собой бесконечно малую более высокого порядка, чем x x0 при x x0 . При этом касательная имеет уравнение

y f (x0 ) f '(x0 )(x x0 ) ) будем называть плоскость касательной к поверхности в точке

(x0 , y0 ,z0 ), если расстояние от точки M(x, y,z)		до этой плоскости есть бесконечно малая
более высокого порядка, чем	x x0 2 y y0	2	при (x, y) (x0 , y0 ).
Рассмотрим некоторую плоскость, проходящую через точку (x0 , y0 ,z0 ):				2
z z0 A(x x0 ) B(y y0)

Из курса аналитической геометрии известно, что расстояние от точки поверхности

(x, y,z(x, y)) до плоскости (2) равно (нормальное уравнение плоскости):

A(x x0 ) B(y y0 ) (z(x, y) z(x0		, y0 ))	3

	A2 B2 1
	A2 B2 1

z z(x0 ,y0 )

(x0, y0 )(x x0 )

(x0, y0 )(y y0 ) 0 (x, y)(x x0 ) 0(x, y)(y y0), 5

где 0 (x, y), 0 (x, y) 0

при (x, y) (x0 , y0 ). Тогда из (3), (4), (5) следует, что

расстояние от рассматриваемой точки до плоскости есть

0 (x, y)(x x0 ) 0 (x, y)(y y0 )

0 (x, y) 0 (x,

(x x0 )2

(y y0 )2 , что

A2 B2 1

представляет собой бесконечно малую более высокого порядка, чем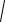(x x0 )2 (y y0 )2 .

Обратно, если есть касательная плоскость (2), т.е.

A(x x0 ) B(y y0 ) (z(x, y) z(x0 , y0 ))

0 (x, y)

x x0

0 (x, y)

y y0

, где , 0

A2 B2 1

при (x, y) (x0 , y0 ) то, раскрывая модуль, получаем, что

z(x, y) z(x0 , y0 ) A(x x0 ) B(y y0 ) (x, y)(x x0 ) (x, y)(y y0 ), где , 0 при

(x, y) (x0 , y0 ), т.е. z - дифференцируемая в точке (x0 , y0 ) функция и

, y

),B

, y

Математический анализ I курс II семестр

Билет 24. Производная по направлению, градиент (стр. 1 из 2)

Билет 24. Производная по направлению, градиент.

Пусть мы снова рассматриваем график функции z z x, y и сечения этой поверхности плоскостями, проходящими через точку M0 x0,y0 плоскости OXY и параллельными оси

Z. В сечениях получаются кривые, проходящие через точку x0, y0,z0 . Проекция такой кривой на плоскость OXY есть прямая линия, проходящая через точку M0 . Будем

обозначать направляющий вектор этой прямой через l, а точки прямой – буквами М. Введём понятие величины отрезка M0M :

M0M длине отрезка M0M со знаком “+”, если M0M и l имеют одинаковые направления;

M0M длине отрезка M0M со знаком “-”, если M0M и l имеют разные направления;

Предположим теперь, что мы рассматриваем некоторую плоскость, на ней фиксируем точку M0 и направление l. Пусть для этой точки плоскости определена величина z M -

функция от точки М.

Важно отметить, что пока мы не вводим никакой системы координат (точки на плоскости, направления и функции от точек можно определить без системы координат).

Рассмотрим теперь точки М, лежащие на прямой, проходящей через M0 в указанном

направлении l и соответствующую величину z M z M0 ; если существует предел этой

M0M

величины при стремлении М к М0 вдоль прямой, то он называется производной z(M) в

точке M0	по направлению l и обозначается	z	M	0	. Как мы видим, в определении

		l

производной по направлению координаты не участвовали. Однако для получения простой формулы для вычисления этой производной удобно ввести систему координат. Итак,

пусть

имеет

координаты x0, y0 ,

–

координаты

x,y ,

имеет

координаты

cos ,sin . Тогда, вводя параметризацию

x x0 tcos ,

y y0

tsin ,

для прямой,

соединяющей

М0

М,

М0М=t

получаем:

z M z M0

z(x0 tcos ,y0

tsin ) z(x0, y0 )

(т.

к.

мы

предположили, что z –

M0M

x0, y0 )

дифференцируема

tcos

tsin

tcos ,y

tsin tcos

0 x0

tsin tsin

tcos ,y0

cos

, y

sin

0 x0

tcos ,y0

tsin cos 0 x0

tcos ,y0

tsin sin .

При

t 0

tcos ,y0 tsin x0, y0

0, 0 0.

Поэтому

z M z M

lim

(x0 , y0 )cos

x0 , y0 sin

z M

0 ,l

(1)

MM0

M M0

Аналогично, в случае 3-х переменных

cos

cos z M

(2)

Скалярное произведение в правых частях (1) или (2) можно представить как

			Математический анализ
			I курс II семестр
		Билет 24. Производная по направлению, градиент (стр. 2 из 2)
			u M0	cos ,	(3)
			u M0	cos ,	(3)

поскольку	l	1, где - угол между и M0 и заданным направлением l .
Мы видим, что выражение (3) имеет наибольшую величину, когда					cos 1. Это

позволяет определить градиент, как вектор, модуль которого равен наибольшей из величин производных по направлению в этой точке. А направление его как раз такое, в котором производная достигает наибольшей величины. Это определение градиента, в котором не участвуют координаты, позволяет рассматривать его как характеристику функции, не зависящую от наблюдателя.

Установим ряд важных свойств градиента: пусть f1 x и f2 x имеют все частные производные 1-го порядка. Тогда

1.f1 x f2 x f1 x f2 x ;

2.cf x c f x ;

3.f1 x f2 x f1 x f2 x f2 x f1 x ;

Если

f2 x 0

, то

;

Если

F u

- функция

одной переменной,

имеющая производную, то

F f x F' f x f x .

Доказательства всех этих свойств аналогичны. Разберем, например, свойство (3). Пусть, для определенности, x x,y,z . Тогда, по правилам дифференцирования,

f1 f2 f1

f1 f2

f2 ,

f1 f2

f1 f2 f2 f1

x,y,z ,

Пусть

y2 z2 .

Найдём

r x2 y2 z2

Для часто встречающихся в физике радиальных функций F r согласно свойству (5)

получаем: F r F' r r F' r r . r

Математический анализ I курс II семестр

Билет 25. Производные высших порядков (стр. 1 из 3)

Билет 25. Производные высших порядков

Если функция

обладает в некоторой окрестности точки

частной производной

, а эта производная обозначается

2 f

. Далее индуктивным образом можно

xi xj

определить производные более высокого порядка. Возникает вопрос: всегда ли

2 f

xi xj

xj xi

Ответ на него такой: нет, не всегда! Можно показать, что функция

x y

, x2 y2

0,0 и

2 f

0,0 .

f x, y

x2 y2

имеет неравные производные

x y

y x

0, x 0, y 0

Однако имеет место следующая теорема.

Теорема 25.1. Пусть

f x, y

определена в открытой области D и пусть в этой

2 f

. Пусть

2 f

области существуют

непрерывны в точке

x y

y x

x y

y x

, y

. Тогда в этой точке

, y

2 f

, y

x y

y x

►Доказательство.

Пусть h,k 0 числа такие, что областьDсодержит все точки из прямоугольника со

сторонами от x0 до x0 h

и от y0

до y0

k .

ПустьW h,k

f x0

h, y0

k f x0

h, y0 f x0 , y0 k f x0 , y0 .

Положим x

f x, y0

k f x, y0

, y

f x0 h, y f x0, y

; тогда

h x

1 y

k y

В промежутке x0 ;x0

h , по условию теоремы, функция x

имеет производную

x, y0 k

x, y0

' x

и, значит, x непрерывна, причем по теореме Лагранжа

h x

1 f

x0 1h, y0

(вновь по теореме

k x

Лагранжа)

2 f

h, y

k , где 0

x y

Математический анализ I курс II семестр

Билет 25. Производные высших порядков (стр. 2 из 3)

С другой стороны, аналогично, получаем

2 f

h, y

k , где 0

y x

0 4 1.

Следовательно, устремляя h,k к 0,0 , получаем, ввиду непрерывности

lim

2 f

, y

lim

2 f

, y

. Таким образом, теорема доказана.◄

x y

h,k 0,0

y x

Замечание. По аналогии можно доказать следующую теорему.

Теорема 25.2. Пусть u f x ,...,x

определена в открытой области D Rn и

имеет в этой области всевозможные частные производные до n-го порядка включительно и смешанные производные k -го порядка, причем все эти производные непрерывны в D. При этих условиях значение любой k -ой смешанной

производной не зависит от того порядка, в котором производится последовательное дифференцирование.

Например,	4	f	4 f		и т.п.
	x2 y2		x y2
				x

25.1.

Дифференциалы высших порядков .

Пусть u f

имеет непрерывные производные в области D Rn . Тогда

dxi

(1)

i 1

При этом, если x1,...,xn

- независимые переменные, то dx1,...,dxn

можно считать

постоянными величинами, не зависящими от

. Поэтому d2 xi 0,

i 1,....,n.

Пусть

f x имеет непрерывные частные производные 2-го порядка. Положим по

определению

d2 f x d df x

dxi

dxidx1 ...

dxidxn

i 1

i 1 xi x1

xi xn

2 f

dxidxj

(2)

x x

i 1

j 1

Здесь мы воспользовались тем, что d2 xi 0.Например:

d2 f x, y

2 f

dx2

2 f

dxdy

2 f

dy2 , при n=2

x y

x,y,z

2 f

dxdy 2

dydz 2

dxdz., при n=3

x y

y z

x z

Математический анализ I курс II семестр

Билет 25. Производные высших порядков (стр. 3 из 3)

Вообще, легко заметить, что, используя формальную операторную запись,

f x

dx1

...

dxn

(3)

Аналогично, полагая dk f d dk 1 f , находим:

							k
							k	f x
dk f		dx1	...			dxn			(4)
dk f		dx1	...	x		dxn			(4)
	x			x	n
	1				n

(В предположении, что для f существуют частные производные до k - го порядка включительно.)

Доказательство этого утверждения можно провести индукцией по k . Мы не будем подробно останавливаться на этом.

Отметим, что если xi xi t1,...,tk (т.е. переменные xi не независимые, а представляют

собой функции от других переменных), то, вообще говоря, они не равны 0 и, хотя ввиду инвариантности 1-го дифференциала, формула (1) сохраняется, уже в формулах (2) и (3) (не говоря о (4)) следует внести изменения.

Именно, вместо (3) в этом случае верна формула

f x

...

(5).

i 1

«Добавок» по отношению к (3) получается, из-за того (см. вывод (2)), что в нашем случае

dxidx1 ...

dxi

Однако, если xi

ai,1t1

... ai,ktk

	f		2
	f		2
		d		xi .
dxidxn		d		xi .
	xi
,				(6)

то dxi ai,1dt1 ... ai,k dtk и d2 xi d const 0. Поэтому в случае линейной замены переменных (6) формулы (3) и (4) сохраняются.

25.2. Второй дифференциал функции.

Вернемся к формуле (2). Она означает, что второй дифференциал является квадратичной формой от переменных dx1,...,dxn . Как известно из курса алгебры,

квадратичной форме сопоставляется матрица квадратичной формы, в рассматриваемом случае называемая иногда матрицей Гессе и имеющая вид

2 f			2 f		2 f


x12		x1 x2		x1 xn
						.

	2 f				2 f

	x x		n		x2
	1		n		n

Математический анализ I курс II семестр

Билет 26. Формулы Тейлора (стр. 1 из 1)

Билет 26. Формула Тейлора

Теорема 26.1.

Пусть функция f x имеет непрерывные производные до n-го порядка включительно в окрестности U x0 точки x0 и непрерывные производные порядка

n 1

в U

. Тогда для любой точки

существует число ,

0 1 такое,

d2 f

dn f

d n 1

что

...

(1)

n 1 !

где все дифференциалы вычислены при

(2).

►Доказательство.

Соединим

в пространстве

точку

с точкой

прямолинейным отрезком;

t имеет вид

запишем параметрические уравнения этого отрезка: любая его точка

x t

(3)

При t 0 получаем

, при t

1 получаем

Рассмотрим функцию одной переменной

F t f

t ,

определенную на

отрезке

t 0,1 .

Поэтому,

при

вычислении

dk F 0

получаем,

соответствии с

билетом

25,

что

dk F 0 dk

k 1,...,n.

(4)

dn 1F dn 1 f

(5)

Осталось применить к функции F t теорему 25.1:

F 1 F 0 F 0 dF 0 d2F 0 ...

dnF 0

dn 1F

(6)

n 1!

Подставляя в (6) из (4) и (5), получаем утверждение теоремы.◄

Теорема 26.2.

Пусть

функция

имеет

непрерывные

производные

до

порядка

включительно

точки

0 .

Тогда

dn f

i 1

...

x x

, где x x .

Для доказательства достаточно использовать теорему 26.1.

Математический анализ I курс II семестр

Билет 27. Экстремумы функций нескольких переменных (стр. 1 из 3)

Билет 27. Экстремум функции нескольких переменных.

Пусть f x определена в окрестности точки x0 Rn . Будем говорить, что x0 - точка минимума (строгого), если для всех xиз некоторой проколотой окрестности U x0

f x f x0 . Точка x0 - точка максимума, если для всех x U x0 f x f x0 . Точки

минимума и максимума обычно называются точками экстремума.
Теорема 27.1. Если		0 - точка экстремума и существует	f		0 , то	f		0 0 .
	x			x			x
			xi			xi

►Доказательство.

Рассмотрим точки, у которых все координаты, кроме i - ой фиксированы и равны координатам точки x0 , а координата xi меняется. Тогда функцию

f x10 ,..., xi0 1,xi ,xi0 1,..., xn0 можно рассматривать как функцию от этой точки. Поэтому

производная этой функции равна 0. Вместе с тем она, по определению, есть f x0 .

Теорема доказана.◄

Замечание 1. Разумеется, в точке экстремума частные производные могут и не существовать.

Пример. z 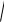x2 y2 , x0 , y0 0,0 . Эта точка, очевидно, точка минимума, т.к. если хотя бы одно из чисел x, y было отлично от 0, величина z 0. Но z x,0 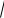x2 x и z 0, y 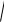y2 y , поэтому частные производные в точках x 0 и y 0 не существуют.

Замечание 2. Если все частные производные в точке экстремума x0 существуют, то все они равны 0 и f x0 0, а также df x0 0, как функция от dx1,...,dxn .

Замечание 3. В точке экстремума дифференцируемой функции z x, y касательная плоскость параллельна плоскости OXY .

27.1. Достаточные условия экстремума.

Сначала мы изложим схему исследования функции f x на экстремум. Прежде всего,

найдем стационарные точки x0 , т. е. такие, что f x0 0 (или df x0 0). Затем,

предполагая, что f x имеет частные производные до 2-го порядка включительно, непрерывные в стационарных точках, применим в этих точках формулу Тейлора

0 df

d2 f

0 1

0 ai, j

xi xj , где

aij

i 1

j 1

при

(Поскольку x - точка, близкая к 0, а производные 2-го порядка непрерывные и df x0 0.) Таким образом, знак приращения совпадает со знаком 2-го дифференциала.

Математический анализ I курс II семестр

Билет 27. Экстремумы функций нескольких переменных (стр. 2 из 3)

Второй дифференциал есть квадратичная форма от x1,..., xn . Если это – положительно определенная форма, то f x0 0 и в точке x- минимум. Если отрицательно определенная, то - максимум. Если форма неопределенная (т.е. меняет знак), то экстремума нет. Для выяснения вопроса определенности формы можно использовать критерий Сильвестра из курса линейной алгебры.

Для этого следует рассмотреть определитель (гессиан)

f11 f1n

, где

fij

обозначают производные

2 f

0 и его главные миноры,

xi xj

f1n fnn

т.е. f

f11

f12

f11 f12 f13

f11

f1n

,...,

Если все эти миноры положительные, то x0 - точка минимума.

Если знаки этих миноров чередуются, начиная со знака «-» - то x0 - точка максимума.

В двумерном случае имеем геометрическую иллюстрацию. При данных условиях в окрестности точки экстремума график функции z z(x, y) имеет вид «почти» эллиптического параболоида:

В случае точки минимума

Математический анализ I курс II семестр

Билет 27. Экстремумы функций нескольких переменных (стр. 3 из 3)

В случае точки максимума

Если же график «почти» гиперболического параболоида (седло), то экстремума нет.

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 119 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
08.04.201516.92 Mб619CFA Level 1 (2009) - 1.pdf
#
08.04.20157.1 Mб233CFA Level 1 (2009) - 2.pdf
#
08.04.20159.18 Mб705CFA Level 1 (2009) - 3.pdf
#
08.04.201510.48 Mб375CFA Level 1 (2009) - 5.pdf
#
03.05.201512.77 Кб26Charisma.docx
#
08.04.20151.57 Mб59chirskii-lectures-2sem.pdf
#
08.04.20153.67 Mб60chirskii-lectures-4sem.pdf
#
08.04.2015182.57 Кб17CHOVUSH1.pdf
#
09.09.2019122.88 Кб16Chto_est_filosofia.doc
#
08.04.2015179.2 Кб16Cмысловое строение социального мира.doc
#
08.04.2015168.12 Кб18deloproizvodstvo--konspekt-....pdf