шпоры
.doc
|
§6. Вычисление пределов. Практические советы.
f(x)/g(x) б.м. при xx0, g(x)/f(x) б.б. при xx0.
Если р = 0, то f(x) величина большего порядка малости, чем g(x) при xx0 f(x)=o(g(x))
Если р = , то f(x) величина меньшего порядка малости, чем g(x) при xx0 g(x)=o(f(x))
Если р = С, то f(x) и g(x) величины одного порядка малости при xx0 g(x)=О(f(x)) или f(x) Cg(x). Таблица эквивалентностей.
Если x0 0, то можно сделать замену переменной у = xx0 0, откуда х = у + х0
При x предел отношения степенных функций зависит от старших степеней, при x 0 от младших.
|
14, Определение производной.
f(x0, x) = f(x0 + x) – f(x0) – приращение y = f(x) , соответствующее приращению x. Производная
1-го порядка функции y
= f(x)
в точке x0
– это
число
f(x0) f-(x0), f+(x0) и f-(x0) = f+(x0) f(x0) f(x) непрерывна в точке x0
Таблица производных основных элементарных функций.
1. (xa)/ = axa1, a 0. 2. (ax)/ = ax lna, a > 0,a 1; (ex)/ = ex. 3. (logax)/ = logaе /x, a > 0,a 1; (ln x)/ = 1/x. 4. (sin x)/ = cos x. 5. (cos x)/ = sin x. 6. (tg x)/ = 1/cos2x. 7. (ctg x)/ = 1/sin2x. 8.
(arcsin
x)/
= (arccos
x)/
=
16. Дифференцирование функций, заданных неявно или параметрически.
Функция y = f(x), x(a,b) неявно задана уравнением F(x,y) = 0, если x(a,b) F(x,f(x)) = 0 (1)
Пусть заданы x = (t), y = (t), t(a,b) (2). Если
t
= 1(x),то
определена y(x)
= (1(x)),
заданная параметрическими соотношениями
(2)
|
|
15. Правила дифференцирования.
1.
(С)/
= 0.
2. (f(x)
+ g(x))/
= f/(x)
+ g/(x).
3. (Cf(x))/
= Cf/(x).
4. (f(x)g(x))/
= f/(x)g(x)
+ f(x)g/(x).
5.
6. Пусть f(x) имеет производную в т. x0, а z = g(y) – в т. y0 = f(x0) z = g(f(x)) в т. x0 имеет производную z/(x0) = g/(y0) f/(x0) – правило дифференцирования сложной функции.
7.
Логарифмическая производная.
|
17.Геометрический, механический, экономический смысл производной.
Уравнение касательной в точке М(х0,у0) y – y0 = f/(x0)(x – x0), нормали x – x0 + f/(x0)( y – y0) = 0
Скорость изменения экономических величин х – затраты ресурса, f(x) выпуск продукции f/(x) предельный продукт х – объем продукции, f(x) издержки производства f/(x) предельные издержки
|
|
18.Дифференциал.!!!
дифференцируемой в точке х0 у(х0,х) = Ах + о(х) (1) Дифференциал Ax = dy(х0,х) = dy(х0,dх) y = f(x) дифференцируема в т.x0 f/( х0) A = f/( х0) y dy при x<<1 y(х0+х) y(х0) + f/( х0)х
20. Раскрытие неопределенностей. Правила Лопиталя.
Теорема
5 (Лопиталь)
f,gC1(U),
g/(x)
0 в
U.
0. - см. «Вычисление пределов. Полезные советы»
. Если f(x)
и g(x)
обе б.б., то Если k 1 , то исходный предел = , если k = 1, то получается .0.
Если y = f(x)g(x) , то ln y = g(x).ln f(x) (0. или .0).
|
19. Теоремы Ферма, Ролля, Лагранжа, Коши.
Теорема 1 (Ферма). f(x) задана на <a,b>, дифференцируема в точке c и f(c) – экстремум f/(c) = 0 Доказательство (идея) f/+(c) = lim( / + ) 0, f/-(c) = lim( / + ) 0
Теорема 2 (Ролль). fC[a,b], fC1(a,b), f(a) = f(b) c(a,b): f/(c) = 0 Доказательство (идея) 1.M = f(x)наиб m = f(x)наим 2. M = m f/(x) 0. 3. Mm одно из этих двух чисел достигается внутри [a,b], в точке c(a,b). 4. По теореме 1 в этой точке f/(c) = 0
Теорема 3 (Лагранж). fC[a,b], fC1(a,b) c(a,b): f(b) – f(a) = f/(c) (b – a) Доказательство (идея) 1.Находят вспомогательную функцию (x) = f(x) +kx: (a) = (b) 2. По теореме 2 c(a,b): /(c) = 0 Теорема
4
(Коши).
f,gC[a,b],
f,gC1(a,b),
g/(x)
0
c(a,b):
|
|
21. Формула Тейлора.
Теорема 6 (Тейлора) f(n+1)(x) U(a) = x xa< x U(a)
a
= 0
|
|
22. Возрастание и убывание функции. Экстремум.
y = f(x) возрастает (убывает ) на (a,b) , если x1 < x2 f(x1) < f(x2) ( f(x1) > f(x2) ) Теорема 1. Если fC1(a,b), f(х)>0 x(a,b), то f(x) возрастает на (a,b) (f<0 убывает) Док-во. По теореме Лагранжа f(x2) – f(x1) = f(x0)(x2 – x1), x0(x1,x2) (a,b) Если окрестность U(x0) точки х0: xx0, x U(x0) f(x) > f(x0), то х0 – т. минимума f(x) < f(x0), то х0 – т. максимума – экстремумы. Необходимое условие экстремума. х0 – т. экстремума f(х0)=0 или не существует Достаточное условие экстремума.
Стационарная точка. Критическая точка. Наибольшее и наименьшее значения непрерывной функции на отрезке достигаются или в критических точках или на концах отрезка.
|
23. Направление выпуклости. Точки перегиба.
График y = f(x) наз. выпуклым вниз (вогнутым вверх) на (a,b), если дуга кривой выше касательной х(a,b) (например, у = х2) Теорема 2. Если fC2(a,b), f(х)>0 x(a,b), то график f(x) является выпуклым вниз на (a,b) f(х) <0 x(a,b), то график f(x) является выпуклым вверх на (a,b) Точка перегиба. Необходимое условие перегиба. х0 – т. перегиба f(х0)=0 или не существует Достаточное условие перегиба. fC2(U(x0)). Если в (х0 , х0) и (х0, х0 + ) f(х) имеет противоположные знаки, то х0 – т. перегиба.
.Асимптоты.
Для y = f(x) прямая, расстояние от т. М( x,f(x) ) до этой прямой 0 при бесконечном удалении т.М от начала координат – асимптота графика. а) Если при этом x a , то полупрямая х = а (y > 0 или y < 0) – вертикальная асимптота. б) Если при этом x + или x , то график имеет наклонную асимптоту. Свойства.
1.
вертикальная асимптота
хотя бы один из
2. Непрерывные на всей оси функции не имеют вертикальных асимптот.
3.
наклонная асимптота y
= kx
+ b
2 предела:
|
|
24. Общий порядок построения графика.
1. Область определения 2. Симметрия (в случае симметричной О.О.) Периодичность Нули (корни) – точки пересечения с осью Ох, точка пересечения с осью Оу. Промежутки знакопостоянства (где график выше оси, где ниже). Поведение вблизи точек разрыва (устранимые, 1-го и 2-го рода). Поведение на бесконечностях (наклонные или горизонтальные асимптоты) 3. Затем, с помощью 1-й производной – интервалы монотонности и точки экстремума. С помощью 2-й производной – интервалы выпуклости и точки перегиба.
|
25.Численное решение уравнений. Метод Ньютона. Метод Ньютона сходится быстрее, чем метод хорд. Корень x0(a,b) уравнения f(x)= 0 изолирован на [a,b] , если на этом отрезке не содержится других корней этого уравнения. [a,b] – отрезок изоляции корня.
Пусть на отрезке [a,b] изоляции корня уравнения f(x)= 0 выполняются условия а) f(x), f(x), f(x)C[a,b], б) f(a).f(b)<0, в) f(x), f(x) не меняют своего знака.Метод хорд. Определим числа xn равенствами
f(x)
= x3
+
2x
– 2. f(0)
= 2,
f(1)
= 1
отрезок изоляции корня [0,1].
f(x)
> 0, f(x)
> 0 на
(0,1)
x0
= 1,
26. Действия над комплексными числами.
Комплексное число
z
характеризуется парой вещественных
чисел (a,b)
с установленным порядком следования
z
= (a,b),
a
= Re
z
– вещественная часть, b
= Im
z
– мнимая часть.
Сумма комплексных чисел z1+z2 = (a1+a2, b1+b2) Свойства. 1. z1+z2 = z2+z1 2. (z1+z2)+ z3 = z1+(z2+ z3) Произведение z1.z2 = (a1a2 b1b2, a1b2 + a2b1) Свойства. 1. z1.z2 = z2.z1 2. (z1.z2). z3 = z1.(z2. z3) 3. (z1+z2). z3 = z1.z3+ z2.z3 (a,0)a. z z.(1,0) = z. (1,0)1. (0,b) – чисто мнимое число, (0,1) i – мнимая единица (0,b) = (b,0).(0,1) bi, i2 = 1 z = (a,b) = a + bi алгебраическая форма записи комплексного числа
Деление
комплексных чисел z
= a
+ bi
=
Геометрическая интерпретация комплексных чисел. z = a + bi отождествляют с точкой x = a, y = b. Плоскость – комплексная, ось Ох – вещественная, ось Оу – мнимая. Множество С множество точек комплексной плоскости множество свободных векторов. При переходе к полярным координатам получают тригонометрическую форму комплексного числа z = r ( cos + i sin ) r = z- модуль, = Arg z – аргумент. arg z [ -, ) или [ 0, 2 ) Arg z = arg z + 2kСвойства. z1 + z2z1 + z2, z1 – z2z1 z2, z a, z b Формулы Эйлера и Муавра.Формула Эйлера ei = cos + i sin z = r ei показательная форма записи комплексного числа.При умножении комплексных чисел их модули умножаются, а аргументы складываются.z1.z2 = r1 (cos 1 + i sin 1 ) .r2 (cos 2 + i sin 2 ) = r1r2 ( cos(1 + 2 ) + i sin(1 + 2 )), r1ei.r2ei = r1r2ei(+)В частности, если z1 = z2 = z, то z2 = r2 (cos 2 + i sin 2), … , zn = rn (cos n + i sin n) cos n + i sin n = (cos + i sin )n – формула Муавра При
делении …Извлечение корня из
комплексного числа.Если z = z1n , то r =
r1n,
= n1
различные
комплексные числа, которые при
возведении в n–ю
степень равны одному и тому же
комплексному числу z.
Модули этих чисел одинаковы – равны
r1
– т.е. они лежат на окружности. Аргументы
отличаются на число, кратное
Решение алгебраических уравнений. f(z)
= A0zn
+ A1zn-1
+ … +An-1z
+ An
, Ak
R.
(1) Пусть он имеет корень z
= a
+ bi
, b
0
z1
= a
– bi
также его корень.
Комплексные корни многочлена (1) распределяются по парам сопряженных корней. Поскольку
Любой многочлен нечетной степени с вещественными коэффициентами имеет хотя бы 1 вещественный корень. Если n = 2 и D<0, то уравнение имеет 2 комплексно-сопряженных корня.
|

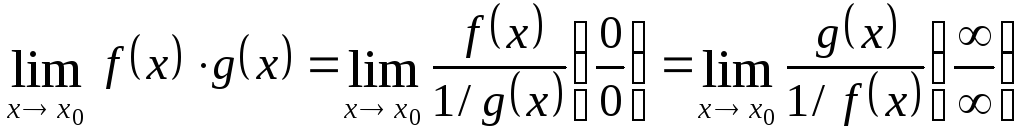
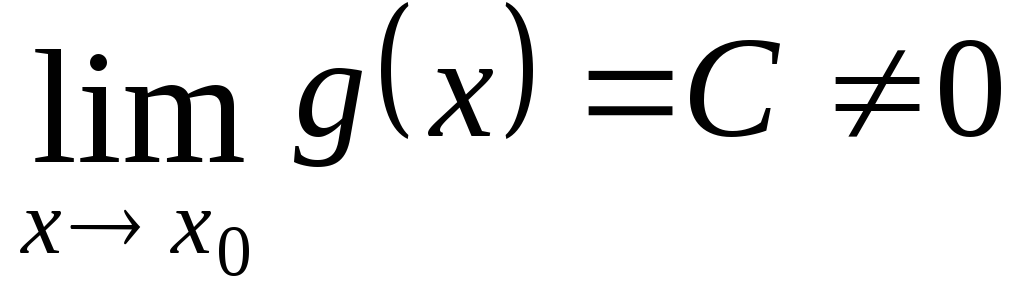 ,
то
,
то
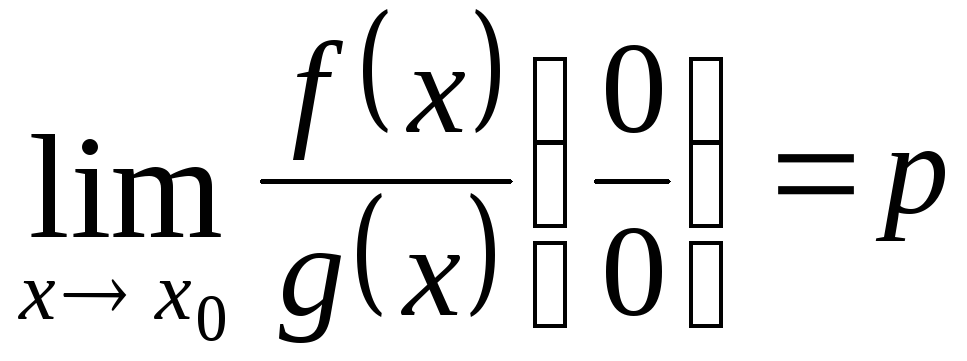
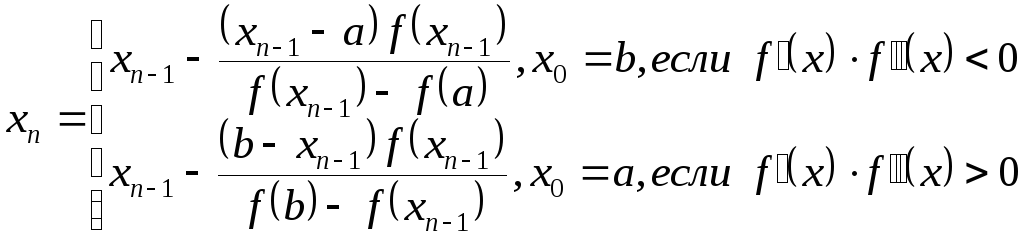 (n=1,2,3,…)
xn
x0
(n),
x0
– корень. Метод
касательных (Ньютона).
Определим числа xn
равенствами
(n=1,2,3,…)
xn
x0
(n),
x0
– корень. Метод
касательных (Ньютона).
Определим числа xn
равенствами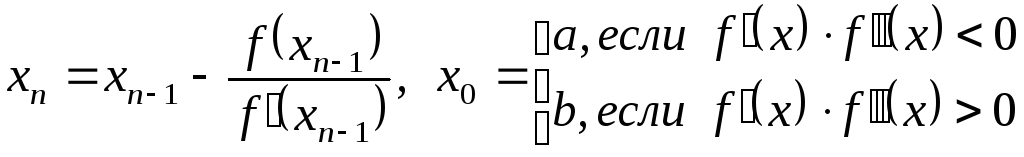 (n=1,2,3,…)
xn
x0
(n),
x0
– корень.
(n=1,2,3,…)
xn
x0
(n),
x0
– корень.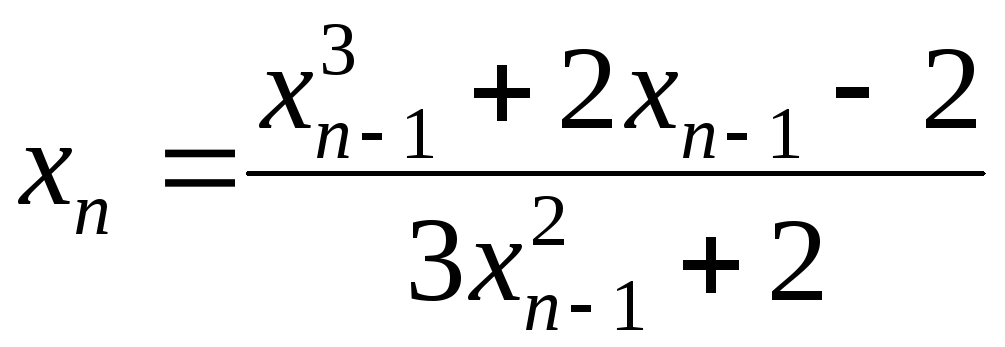 ,
x1
= 0,8; x2
= 0,7714; x3
= 0,7709, x4
= 0,770917
,
x1
= 0,8; x2
= 0,7714; x3
= 0,7709, x4
= 0,770917