Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Башкирский Государственный Педагогический Университет им. М. Акмуллы

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Гайнуллин часть2

.pdf

Скачиваний:

Добавлен:

19.03.2015

Размер:

1.37 Mб

Скачать

☆

<<< < Предыдущая 12 / 92 3 4 5 6 7 8 9 > Следующая >>>

§11. Решение систем и совокупности неравенств с одним неизвестным

Несколько неравенств с одним неизвестным образуют систему неравенств в том случае, если ставится задача об отыскании тех значении неизвестного, которые удовлетворяют одновременно каждому из заданных неравенств.

Несколько неравенств с одним неизвестным образуют совокупность неравенств в том случае, если ставится задача об отыскании тех значении неизвестного, каждое из которых удовлетворяет, по крайней мере, одному из заданных неравенств.

Из этих определений следует, что решением системы неравенств служит пересечение решений неравенств, образующих систему; решением совокупности служит объединение решений неравенств, образующих совокупность (здесь, как и выше, под решением понимается общее решение, то есть множество всех частных решений).

Неравенства, образующие систему, объединяются фигурной скобкой. Так запись

3х −1 > 5,+ <

2х 2 7

означает, что заданные неравенства образуют систему. Иногда система неравенств может быть записана в строчку. Например, система

2	х + 3 < x − 4,
	х + 3 > 3х −1
2	х + 3 > 3х −1

может быть записана следующим образом:

3х −1< 2х + 3 < х − 4.

Неравенства, образующие совокупность, объединяются квадратной скобкой. Так запись

3х −1 > 5,

+ <

2х 2 7

означает, что заданные неравенства образуют совокупность. Совокупность неравенств может быть записана и в строчку, в этом

случае используется знак « ; ». Например, указанная выше совокупность неравенств может быть записана следующим образом:

3х −1> 5; 2х + 2 < 7.

Нестрогое неравенство равносильно совокупности, состоящей из соответствующего строгого неравенства и уравнения. Например, неравенство

f(х) ≥ g(х) равносильно совокупности

f (х) > g(х),

f (х) g(х).

Всякое «неравенство» f (х) ≠ g(х) можно записать в виде совокупности двух строгих неравенств:

f (х) > g(х) f (х) > g(х).

Несколько систем неравенств с одним неизвестным образуют совокупность систем неравенств в том случае, если ставится задача об отыскании тех значений неизвестного, каждое из которых удовлетворяет, по крайней мере одной из данных систем. Аналогично можно говорить о системах совокупностей неравенств.

Выше мы отметили, что при решении систем и совокупностей неравенств с одним неизвестным нам придется искать пересечение и объединение числовых множеств. Это удобно делать с помощью числовой оси.

Пример 1. Решить систему неравенств:

2х2		+ ах < 3а2 ,
	х +			(1)
	х +	а	> 0.	(1)


	х

Решение.

3а

2(х − а) х +

< 0,

а = 0,

> 0,

а < 0,

а = 0,

3а

(1) х(х + а) > 0,

< 0, −

< х < а,

а < x

< −

≠ 0

> 0

< −a x > 0 х < 0

x > −a

> 0,

а > 0,

< 0,

а < 0,

3а

−

< х < −а

< x < a

< x < 0

− а < x < −

Ответ. Если а < 0 , то (a,0) U (−a,−

); если а > 0

,то (−

,−a) U (a,0); ес-

ли а = 0 , то .

Пример 2. Решить дизъюнкцию неравенств:

3 х2 − 6х < −x −3 − х2 + 6х < −x.

Решение.

x < −3,

1) 3 х2 − 6х < −x x2 − 6x < −x3 x(x + 3)(x − 2) < 0

0 < x < 2.

x < −3,

2) − 3 х2 − 6х < −x x2 − 6x < −x3 x(x + 3)(x − 2) <

0 < x < 2.

Ответ. (−∞,−3) U (0,2).

Упражнения.

Решить систему неравенств (523-529):

2х +1

−

2 −

> 1,

− 3 <

+ 5,

523.

524.

> 0.

− х − 2 > 0.

− 4х −1

− 3х −1

< −2,

525.

2х −1

528.

− 5х + 4 ≤ 0.

526.

х2 − 7х +12 ≤ х ≤ х2 + 2х −12.

529.

4х − 3 < х +1,

527.

х + 6 +

4 − х > 4.

lg				> lg(х − 4) − 2lg2,
lg		х + 8		> lg(х − 4) − 2lg2,

		х	2 + 3		> 0.

	х2 −18х + 81
	х2 −18х + 81
	хlg2		+ lg(2х+2 +1) < lg(7 2х+1 +12),

	lg(х + 3)		> 2.


	lg(х +1)

Решить дизъюнкцию неравенств (530-534):

		2х +1		−		2 − х		> 1,
530.				−				> 1,	533.
530.			5		3				533.

	− 4х −1 > 0.
	х		− 3 <		х +1		+ 5,
531.									524.
		2			4
		2			4
			− х − 2 > 0.
	х2		− х − 2 > 0.

	− 3х −1				< −2,
532.		2х −1			< −2,
			− 5х + 4 ≤ 0.
	х2		− 5х + 4 ≤ 0.

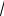х + 3 < x +1 −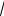х + 3 < x +1.

3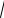х2 − 2х > −x −3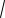− х2 + 2х > −x.

Решить систему неравенств с параметрами (535-540):

535.	ax < 5a − 9,	538.
	x < 3.
536.	2 − 3х > 8a,	539.
	2ах − 6а > x.
537.	(а + 3)(х − 3) > 3(х − 4),	540.
	(а + 2)х > (а +1)x + 5.

х +

,а ≠ 0.

−

а >

2а2

< 2ах + 3а

х2

− ах < 6а2 ,

> 0.

х − 2а

Решить системы неравенств (541-546):

541.	1< 2x		−1< 9,	543.
	−1≤	1	− х ≤ 4.
542.	х2 ≥	9,		544.
542.				544.
	0 < 2x + 9 < 17.

9			≥1,

	х	2
	х
		1
		1		≤ 0.
	х − 2			≤ 0.
	х − 2
			4			<1,

	(х − 2)				2
	(х − 2)
		х2
		х2		≥1.
				≥1.
	х	2	−1
	х		−1

	0 < (x − 2)2 < 25,				1− х2	> 0,
545.	х2	+ 4х + 4	≥ 0.	546.	х −1	+	1	> 0.

		х +1
					2 − х		2
Решить совокупность неравенств (547-550):
547.	−1< x <1,			549.	−1< 2x −1<1,
	0 ≤ х ≤ 5.				0 < х + 2 < 4.
548.	0 < x ≤ 3,			550.	1< 3x − 2 ≤ 4,
	− 2 ≤ х ≤ 0.				− 3 < 4х + 5 <1.

549.−1< 2x −1<1,0 < х + 2 < 4.

100

ГЛАВА V. ТРИГОНОМЕТРИЯ

§ 1. Тождественные преобразования тригонометрических выражений

Напомним основные факты тригонометрии, которые понадобятся в дальнейшем.

I.Некоторые значения тригонометрических функций:

					Аргумент х					π					π			π			π		3π
								0		π					π			π			π	π	3π
								0	6					4			3				2	π	2
									6					4			3				2		2
					Функция

											1
					sinx			0			1			2			3				1	0	-1
									2
														2			2
														2			2

																			1
					cosx			1	3					2					1		0	-1	0
																	2
									2					2
									2					2


					tgx			0	3					1							-	0	-
									3								3

									3
									3


					ctgx			-						1				3			0	0	0
									3									3
									3								3
																	3

II.Знаки тригонометрических функций по четвертям:
	х					четверть			sin x							cos x						tg x		ctg x

	0 < x < π						I					+				+						+		+
	2

		π < x < π					II					+								−		−		−
	2

	π < x <			3π			III						−							−		+		+
	π < x <						III						−							−		+		+
	2

		3π	< x < 2π				IV						−			+						−		−
	2		< x < 2π				IV						−			+						−		−
	2

III. Четность, периодичность.

Функция у = cos х является четной, остальные тригонометрические функции нечетные. Таким образом,

101

cos ( -х) = cos х, sin ( -х) = — sin x,

	π
tg ( -х) = -tg х x ≠		+ πn, n Z ,
	2

ctg ( -х) = -ctg х (x ≠ πn, n Z).

Все тригонометрические функции являются периодическими. При этом Т=2π — основной период функций у =sin х, у =cos x, а Т=π — основной период функций у = tg х, у = ctg х (напомним, что основным периодом называется наименьший из множества всех положительных периодов периодической функции). Таким образом,

sin(x+ 2π) = sin(x−2π) = sinx, cos( x + 2π ) = cos( x − 2π ) = cos x,

	π
tg(x +π ) = tg(x −π ) = tgx x ≠		+πn,n Z ,
	2
ctg(x +π ) = ctg(x −π ) = ctgx (x ≠ πn, n Z).
IV. Формулы, связывающие тригонометрические функции одного и
того же аргумента:
cos2 α + sin2 α = 1,		(4.1)

2	1		π
1+ tg α =		, α ≠		+ πn,n
1+ tg α =	cos2 α	, α ≠		+ πn,n
	cos2 α		2

Z , (4.2)

1	(α ≠ πn, n Z).
1+ ctg2α = sin2 α	(α ≠ πn, n Z).	(4.3)

V. Формулы, связывающие функции от аргументов, один из которых в 2 раза больше другого:

sin 2α = 2sinα cosα,
cos2α = cos2 α − sin2 α,
tg2α =	2tgα	α ≠ π	+ πn	,α ≠ π	+ πk, n,k Z	,

1− tg2α
		4	2	2

ctg2α =	ctg2α −1	α ≠ πn		, n Z	.

	2ctgα
			2

1+ cos2α = 2cos2 α, 1− cos 2α = 2sin2 α,

1± sin 2α = (cosα ± sinα )2.

VI. Формулы сложения аргументов: sin(α ± β )= sinα cosβ ± sin β cosα,

cos(α ± β )= cosα cos β m sinα sin β,


tg(α ± β )=	tgα ± tgβ	α ≠ π + πn, β ≠ π + πk, α ± β ≠ π + πm, n, k,m Z)
tg(α ± β )=		α ≠ π + πn, β ≠ π + πk, α ± β ≠ π + πm, n, k,m Z)
1	± tgα tgβ		2	2	2
ctg(α ± β )=	ctgα ctgβ m 1		(α ≠ πn, β ≠ πk,α ± β ≠ πm, n,k, m Z).
ctg(α ± β )=	ctgβ m ctgα		(α ≠ πn, β ≠ πk,α ± β ≠ πm, n,k, m Z).
	ctgβ m ctgα

(5.1)

(5.2)

(5.3)

(5.4)

(5.5)

(5.6)

(5.7)

(6.1)

(6.2)

(6.3)

(6.4)

102

VII. Формулы приведения:

	π −α	π +α	π −α	π +α		3π	−α		3π	+α	2π −α
	π −α	π +α	π −α	π +α	2		−α	2		+α	2π −α
	2	2			2			2
sin x	cosα	cosα	sinα	− sinα	− cosα			− cosα			− sinα

cos x	sinα	− sinα	− cosα	− cosα	− sinα			sinα			cosα

tg x	ctgα	− ctgα	− tgα	tgα	ctgα				− ctgα		− tgα

ctg x	tgα	− tgα	− ctgα	ctgα	tgα				− tgα		−ctgα

Для облегчения запоминания указанных в таблице формул приведения можно рекомендовать следующее мнемоническое правило:

1) если дуга α откладывается от горизонтального диаметра (π±α

,2π -α ), то название функции сохраняется;

2)если дуга α откладывается от вертикального диаметра (π ±α, 3π ±α )

2 2

то функции синус, косинус, тангенс, котангенс меняются соответственно на косинус, синус, котангенс, тангенс;

3) считая дугу α дугой первой четверти, находят, в какой четверти

расположена дуга πn ±α ( n Z );

4) определяют, какой знак имеет заданная функция в этой четверти, и ставят этот знак перед полученным результатом.

VIII. Формулы преобразования суммы тригонометрических функций в произведение:

sinα + sin β = 2sin α + β cos α − β ,

(8.1)

sinα − sin β = 2sin α − β cos α + β ,

(8.2)

cosα + cos β = 2cosα + β cosα − β ,

(8.3)

cosα − cos β = 2sin α + β sin β −α ,

(8.4)

tgα ± tgβ =

sin(α ± β )

α ≠

+ πn,

β ≠

+ πk, n, k Z , (8.5)

cosα cos

ctgα ± ctgβ =

sin(α ± β )

(α ≠ πn, β ≠ πk, n,k Z),

(8.6)

sinα sin β

(8.7)

cosα ± sinα = 2 cos

IX. Формулы преобразования

произведения

тригонометрических

функций в сумму:

sinα sin β =

sin(α − β )+ sin(α + β )

(9.1)

103

Пример 3. Докажем тождество


cosα cos β =		cos(α − β )+ cos(α + β )		,	(9.2)

2
sinα sin β =	cos(α − β )− cos(α + β )		.		(9.3)

Пример 1. Упростим выражение

sin3 (α − 270o )cos(360o −α ) tg3 (α − 90o )cos3 (α − 270o ) .

Решение. Воспользовавшись четностью функции у =cos x и нечетностью у = tg x, у = sin x, получаем:

−sin3 (270o −α )cos(360o −α )

−tg3 (90o −α )cos3 (270o −α ) .

Применив формулы приведения, получаем:

− cos3 α cosα	=	cos4 α			= cosα.
ctg3α(− sin3 α )		cos3 α	sin3	α

		sin3 α

Исходное выражение тождественно cos а на множестве всех таких α , чтоsinα ≠ 0 и cosα ≠ 0, откуда α ≠ πn (n Z ).

		2
Пример 2. Докажем тождество
	cos2 α			=	1	sin 2α.
	α	− tg	α	=	4	sin 2α.
	α		α		4
	ctg
2			2

Решение. Преобразуем левую часть тождества

cos2 α		=		cos2 α
ctg α − tg α		=	cos α		−	sin α
2	2			2	−		2
			sin	α		cos	α
			sin	2		cos	2
				2			2

		cos2	α		cos α sin α
=				= cos2 α		2	2	.
=	cos2	α − sin2 α		= cos2 α	cos2	α − sin2 α		.
	cos2	α − sin2 α			cos2	α − sin2 α
		2	2			2	2
	cos α sin α
		2	2

Но (см. формулы (5.1) и (5.2))

cosα sin α =		sinα	;	cos2 α − sin2 α = cosα.
cosα sin α =			;	cos2 α − sin2 α = cosα.
2	2	2		2	2

Поэтому

	cosα sin α						1		sinα		1		1
cos2 α			2	2		=		cos2 α		=		cosα sinα =		sin 2α.
									cosα
	cos	2	α	− sin	2 α	2				2		4
			2		2

Осталось найти ОДЗ тождества. Имеем: cos α sin α ≠ 0 и cosα ≠ 0 ,

2 2

то есть sinα ≠ 0 и cosα ≠ 0, откуда получаем: α ≠ πn (n Z ).

104

	tg2 2α − tg2α	= tg3α tgα .
	1− tg2 2α tg2α	= tg3α tgα .
	1− tg2 2α tg2α

Решение. Разложим на множители числитель и знаменатель выражения, содержащегося в левой части тождества

tg2 2α − tg2α		(tg2α −tgα )(tg2α + tgα )		tg2α + tgα	tg2α − tgα
	=		=			.
1− tg2 2α tg2α		(1− tg2α tgα )(1+ tg2α tgα )		1− tg2α tgα	1+ tg2α tgα

Далее, использовав формулы (6.3), получаем

tg(2α +α )tg(2α −α )= tg3α tgα.

ОДЗ тождества определяется			условиями:						α ≠ π + πk ,		2α ≠ π +πn,
										2	2
3α ≠ π +πm , откуда	α ≠ π + πn и α ≠ π + πm					(множество Р всех чисел вида
2	4	2	6	3
π + πk содержится в множестве М всех чисел вида π + πm )(k,n, m Z ).
2									6	3
Пример 4. Докажем тождество
		2cosα − sin 2α		= tg	2		o	−	α
						45			.
		2cosα + sin 2α				45			.
		2cosα + sin 2α							2

Решение. Имеем

2cosα − sin 2α

2cosα − 2sin

α cosα

2cosα(1

−sinα )

(1−sinα )

− cos(90o −α )

2cosα + sin 2α

2cosα + 2sin

α cosα

2cosα(1

+ sinα )

(1+ sinα )

+ cos(90o −α )

Воспользовавшись формулами (5.5) и (5.6), получаем

2sin

−

1− cos(90

−α )

= tg

−

1+ cos(90

−α )

2cos

−

ОДЗ тождества определяется из условий

cosα ≠ 0,1+ sinα ≠ 0 , откуда α ≠ 90 o + 180 o n(n Z ).

Пример 5. Докажем тождество

4sinαsin (60° −α )sin(60° + α ) = sin 3α.

Решение. Здесь целесообразно применить для левой части тождества формулы из группы IX. Имеем

4sinαsin(60° −α )sin(60° + α ) = 4sinα cos(60° −α − 60° −α )− cos(60° −α + 60° + α ) =

								2
= 2sinα[cos(−		o	]=			1
		2α)−cos120		2sinα cos2α +				= 2sinα cos2α +sinα =

						2
= 2	sin (α − 2α )+ sin (α + 2α )				+ sin α		= −sinα + sin3α + sinα = sin3α

ОДЗ тождества – множество всех действительных чисел.

Упражнения.

Упростите выражения (551-566):

105

	2cos(π −α)sin(π + α)tg(π −α)
551.	2		2	.
551.	ctg(	π	+ α)sin(π −α)	.
	ctg(	π	+ α)sin(π −α)
		2

sin(3π + α)tg(π + β )

552.			2	2				.
552.						3π		.
	cos(π −α)ctg(					3π	− β )
	cos(π −α)ctg(						− β )
				2
	ctg α + tg α
553.		2		2	.
553.		α			.
	ctg	α	− tg	α
	ctg		− tg

554.2cosec4α − ctg2α.

555.tg2 (45o + α) −1. tg2 (45o +α) +1

556.tg(π + α ) 1− sinα . 4 2 cosα

557.

2cos2 α −1

2tg(

π − α)sin2 (π + α)

Докажите тождества (567-585):

567.

sin(β − γ )

sin(γ −α)

sin(α − β )

= 0.

cosβ cosγ

cosγ cosα

cosα cos β

568.

sin2

3α

−

cos2 3α

= 8cos2α.

sin2 α

cos2 α

569.3(sin4 х + cos4 х) − 2(sin6 х + cos6 х) = 1.

570.cos3 α − cos3α + sin3 α + sin3α = 3.

αsinαcos

571.	cos2α	=	1	− tgα	.
	+ sin 2α
1		1		+ tgα

572. 1− sin8α = 2cos2 (45o + 4α).

	cosα − sin α			1
573.	2	2	=	1			− tgα.
573.	α	α	=		cosα		− tgα.
	α	α			cosα
	cos	+ sin
	2	2
574.	ctgα + cosecα			=		2cosα		.
574.	sinα + tgα			=				.
	sinα + tgα			1		− cos2α

575.tg2 (45o + α ) = secα + tgα . 2 secα − tgα

576.2(cosec2α + ctg2α) = ctg α − tg α .

2 2

577.1− 2cos2 ϕ = tgϕ − ctgϕ. sinϕ cosϕ

106

558.

cos2 (α + β ) + cos2 (α − β ) − cos2αcos2β.

559.			sinα + sin3α + sin5α																	.
559.			cosα + cos3α + cos5α																	.
			cosα + cos3α + cos5α
										π
						2
						2
560.											= 2arctg( 2								−1).
560.											= 2arctg( 2								−1).
						2				4
						2				4
561.					2 − sinα − cosα											.
561.																.
							sinα − cosα
562.		cos4α + 4cos2α + 3.
563.					sin 4α								cos2α						.
563.				+ cos4α									+ cos2α						.
		1		+ cos4α								1	+ cos2α
564.					sin2 2α − 4sin2 α
																		.
			sin2 2α + 4sin2 α − 4															.
565.		sin2 (π + α ) − sin2 (π − α ).
									8		2				8					2
		f (x) ≥ 0
566.													.
								f (x) > g(x)

578.
				+				π						π					4sin		2	α − 3.
4sin α				+						sin		α −			=				4sin			α − 3.
									3					3
579.
	sinα + sin β													= sin(α + β )sin(α − β ).
	α + β							+ ctg			α −		β							2cosβ
	tg							+ ctg
2												2
580.
	2sinα − sin3α + sin5α																= −			2cos2α			.

	cosα − 2cos2α + cos3α																			tg		α
																				tg		2
																						2
581.

cosα + cos(120o −α) + cos(120o + α) = 0.

582.

tg(35o +α)tg(25o −α) = 2cos(10o + 2α) −1. 2cos(10o + 2α) +1

583.

tg3α = tgαtg(60o + α)tg(60o −α). 584. 3 − 4cos2α + cos4α = 8sin4 α.

585.

cosα cos2α cos4α cos8α cos16α = sin32α . 32sinα

<<< < Предыдущая 12 / 92 3 4 5 6 7 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.03.2015396.29 Кб55Все формулы площади плоских фигур.doc
#
09.11.2019216.58 Кб1Высшая математика лекции.doc
#
13.08.2019743.42 Кб5Г. В. Ф. Гегель Философская пропедевтика.doc
#
13.08.2019628.74 Кб3Г.В. Андрейченко, В.Д. Грачев - Философия (2001...doc
#
07.03.201642.9 Кб15Газизова Л.Ф., Нухова М.В. Психологические особенности стилей воспитания в родных и приемных семьях.docx
#
19.03.20151.37 Mб32Гайнуллин часть2.pdf
#
07.03.2016168.96 Кб22гак лексикология 1.doc
#
18.03.2015127.91 Кб27ГАК.docx
#
19.11.201866.38 Кб5ГАЛАКТИКА.docx
#
03.11.20181.8 Mб2галина.doc
#
27.11.2019336.38 Кб6ГГГ.doc